Straight Lines - Definition, Equations, Properties and Examples

Look around you!! Most of the objects around you are made of lines among which most of them are straight lines. Straight lines are in a Book, a table, a cupboard, a door and so on. Most of the shapes are made of straight lines.

In mathematics, a straight line is an infinite length between two points without any curves. Straight lines are under the topic of analytical geometry in Mathematics. Analytical Geometry has many applications in various fields like Engineering, Architecture, etc. This article is about the concept of straight lines.

What is a Straight Line?

A straight line is an infinite length extending in both directions. Every equation of the first degree in $x, \text{and} \space y$ represents a straight line. The general equation of a straight line is given as $ax+b y+c=0$ where $a, b,$ and $c$ are real numbers and at least one of $a$ and $b$ is non-zero.

Types of Straight Lines

The types of straight lines based on its position and relation with other lines are mentioned below:

Properties of Straight Lines

The properties of straight lines include,

• The length of the straight line is infinite

• A straight line gives the shortest distance between two points

• Straight lines do not have any curves or bends.

• Straight lines are one-dimensional

• A straight line does not have area or volume

Slope of a Straight Line

In mathematics, the change of the $y$-axis coordinate with respect to the change of the $x$-axis coordinate is called the Slope of a line. It is the ratio of vertical change to horizontal change between two points on a line. It measures the steepness and direction of the line. The slope of a straight line is denoted by $m$.

• The slope of a line with given two points $(x_1,y_1)$ and $(x_2,y_2)$ is $m = \frac{y_2-y_1}{x_2-x_1}$

• The slope of a line with a given angle $\theta$ is $ m = \tan \theta $

• The slope of a line from the equation of the line of the form $y=mx+c$ is the coefficient of the variable $x$, which is $m$.

Types of Slopes

Slope of a straight line can be of different types.

• Uphill slopes

• Downhill slopes

• Horizontal slopes

• Vertical slopes

Uphill Slopes

The slope of a straight line extending upwards from left to right is called the uphill slope. It is also called a positive slope as the calculated slope will yield a positive value. In this type of slope, when the value of $x$ increases, the value of $y$ also increases.

Downhill Slope

The slope of the straight line extending downwards from left to right is called the downhill slope. It is also called a negative slope as the calculated slope will yield a negative value. In this type of slope, when the value of $x$ increases, the value of $y$ decreases.

Horizontal Slope

The slope of a horizontal line is called the horizontal slope. This is also called a zero slope as the calculated slope will yield the value $0$. In this type of slope, when the value of $x$ increases, the value of $y$ remains the same. That is, the line remains flat.

Vertical Slope

The slope of a vertical line is called the vertical slope. This is also called an infinite slope as the slope is undefined. In this type of slope, when the value of $y$ increases, the value of $x$ remains the same. That is, the line will be straight up or down.

Notes:

• The slope of a horizontal line is $0$

• The slope of a vertical line is undefined

• The slope of parallel lines $l_1$ and $l_2$ with slopes $m_1$ and $m_2$ is equal (i.e) $m_1 = m_2$

• The product of the slope of two perpendicular lines $l_1$ and $l_2$ with slopes $m_1$ and $m_2$ is $1$ (i.e) $m_1.m_2 = 1$

Equation of a straight line

The equation of straight line in various forms are point-slope form, slope-intercept form, standard form, etc. These forms help us understand how to find the equation of a straight line with the given information. Let’s discuss each form in detail.

Equation of Horizontal and Vertical lines

• Horizontal Line: A horizontal line has a slope of zero. Its equation is of the form $y = c$, where $c$ is the $y$-coordinate of any point on the line.

• Vertical Line: A vertical line has an undefined slope. Its equation is of the form $x = a$, where $a$ is the $x$-coordinate of any point on the line.

Example: $y=2$ is a horizontal line and $x=4$ is a vertical line.

Point-slope form of Straight line

The point-slope form is used to determine the equation of a straight line passing through a point $(x_1,y_1)$ and having slope $m$. The point-slope form of straight line is given by $y-y_1=m(x-x_1)$

Example: The straight line equations with $m = 2$ and passing through $(3,4)$ is

$(y-4)=2(x-3)$ ⇒ $2x-y=2$

Two points form of a line

The straight line equations passing through $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$\frac{x-x_1}{x_1-x_2}=\frac{y-y_1}{y_1-y_2}$

Example: The equation of a line passing through $(1,2)$ and $(3,5)$ is

$\frac{x-1}{1-2}=\frac{y-3}{3-5}$

⇒ $2x-2=y-3$

⇒ $2x-y+1=0$

Slope intercept form of a line

If a line is given with its slope m and its $y$-intercept. Say, a line intersects the $y$-axis at the point $(0, c)$. Using the point-slope form of straight line, we have $y - c = m (x - 0) ⇒ y = mx + c$, where $c$ is the $ y$-intercept. This is called the slope-intercept form of a line.

Example: The equation of a line with slope $m=3$ and $y$-intercept $4$ is $y=3x+4$.

Intercept form of a line

The intercept form is used when the intercepts on the $x$-axis and $y$-axis are known. It is given by: $\frac{x}{a}+\frac{y}{b}=1$, where $a$ is the $x$-intercept and $b$ is the $y$-intercept.

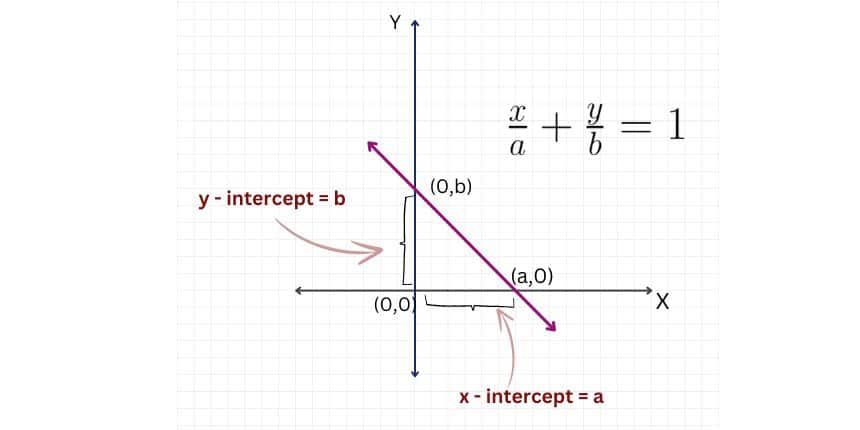
Example: For $x$-intercept as $4$ and $y$-intercept as $5$, the equation of line becomes $\frac{x}{4}+\frac{y}{5}=1$

The normal form of a line

The normal form of a line’s equation involves the perpendicular (normal) distance from the origin to the line. It is given by: $x\cos\alpha + y\sin\alpha=p$

Where $p$ is the length of the perpendicular from the origin to the line, and $\alpha$ is the angle between this perpendicular and the positive $x$-axis.

Example: For $p=5$ and $\alpha=30°$, the equation of the line becomes

$x\cos 30° + y\sin 30° = 5$ ⇒ $\sqrt{3}x+y=10$

Standard form of a line

The standard form of a straight line is given by $ax + by + c = 0$, where $a, b, c$ are real numbers.

Example: The equation of a line in standard form is $2x + 3y + 5 = 0$.

Important Formulas for Straight Lines

The important formulas for straight lines include the angle between two straight lines and the distance between two points on a line.

Angle Between Two Straight Lines

The angle($θ$) between two lines with slopes $m_1$ and $m_2$ can be found by using the formula:

$\tan θ = \frac{m_1-m_2}{1+m_1m_2}$

If the value of $\frac{m_1-m_2}{1+m_1m_2}$ is positive, then the angle between the lines is acute.

If the value of $\frac{m_1-m_2}{1+m_1m_2}$ is negative, then the angle between the lines is obtuse.

Distance between Two Points on a Line

The distance between two points on a line $(x_1,y_1)$ and $(x_2,y_2)$ is $d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$

List of Topics According to NCERT/JEE MAIN

Importance of Straight Lines

Straight lines are an important concept in analytical geometry. The properties of straight lines are very important to determine the properties of other shapes and structures in geometry. The straight line graphs can be used in the fields of study as diverse as business, economics, social sciences, physics and medicine.

How to Study Straight Lines?

Start preparing by understanding the slopes of a straight line. Try to be clear on important formulas for straight lines like the slope of a straight line, the angle between two straight lines and the equation of straight line in various forms. Practice many problems from each topic for better understanding.

If you are preparing for competitive exams then solve as many problems as you can. Do not jump on the solution right away. Remember if your basics are clear you should be able to solve any question on this topic.

Important Books for Straight Lines

Start from NCERT Books, the illustration is simple and lucid. You should be able to understand most of the things. Solve all problems (including miscellaneous problems) of NCERT. If you do this, your basic level of preparation will be completed.

Then you can refer to the book Arihant's Skills in Mathematics Coordinate Geometry by Dr. SK Goyal. Straight Lines are explained very well in these books and there are an ample amount of questions with crystal clear concepts. Choice of reference book depends on person to person, find the book that best suits you the best, depending on how well you are clear with the concepts and the difficulty of the questions you require