AP, GP and HP Full Form

What is the full form of AP, GP and HP?

AP stands for Arithmetic progression, GP stands for Geometric progression and HP stands for Harmonic progression. These are important topics used in a variety of competitive exams. A progression is a particular kind of sequence for which it is easy to find a formula for the nth term. The arithmetic progression is the most widely used mathematical progression, using simple formulas. It refers to a mathematical sequence where the difference between two consecutive terms is always a constant. The term "finite arithmetic progression" refers to a finite portion of an arithmetic progression, and an arithmetic series is referred to the total of a finite arithmetic progression.

Main Terms Of Arithmetic Progression

• The first term is denoted by "a".

• The common difference is denoted by "d".

• The nth term, which is denoted by an.

• Sum of the first "n" terms which is denoted by Sn.

Formulas Of Arithmetic Progression

There are two most commonly used formulas of AP-

• To find the nth term of AP, which is given by the formula-

a_{n}=a+(n-1)d

• And to find the Sum of the first nth term, which is given by-

S_{n}=\frac{n}{2}[2a+(n-1)d

Types Of Arithmetic Progression

There are mainly two types of arithmetic progression-

• Finite arithmetic progression contains a finite number of terms, i.e. it has the last term.

• Infinite arithmetic progression, which does not contain any last term.

Geometric Progression

It is a sort of sequence in which each successive term is created by multiplying each preceding term by a fixed number which is known as the common ratio. Generally, it is represented as-

a, ar, ar2, ar3… an-1 where "a" is the first term, "r" is the common difference and an-1 represents the nth term.

Formula To Find "nth" Term In Geometric Progression

a_{n}=ar^{n-1}

Harmonic Progression

The reciprocal of the terms in the arithmetic progression generates the harmonic progression. The terms of the harmonic progression (or harmonic sequence) are-

\frac{1}{a},\frac{1}{a+d},\frac{1}{a+2d}

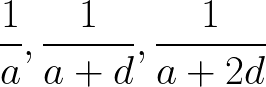
If the provided terms of the arithmetic progression are a, a+d, a+2d, etc.

Formula For "nth" Term Of Harmonic Progression

n^{th}=\frac{1}{[a+(n-1)d]}