Cryptography is a fascinating field that has captured the attention of mathematicians, computer scientists, and security experts alike for decades. At its core, cryptography is the art of secure communication, and it plays a critical role in modern society. From securing online transactions to protecting confidential information, cryptography is everywhere.

The mathematics behind cryptography is the key to unlocking its secrets. The use of mathematical concepts and algorithms to encrypt and decrypt information is what makes cryptography so powerful. However, cryptography is not just about applying mathematical formulas; it requires a deep understanding of mathematical concepts and a creative approach to problem-solving.
In this article, we will try to understand cryptography and explore the role that mathematics plays in its design and implementation. We will discuss the history of cryptography, the basic principles of encryption and decryption, and the different types of cryptographic algorithms used today. We will also examine some of the challenges facing cryptographers, such as quantum computing and the threat of cyber attacks.
Whether you are a mathematician, a computer scientist, a security expert, or simply someone interested in the fascinating world of cryptography, this article is for you. So, let's dive in and unlock the secrets of cryptography!
The History Of Cryptography
The origins of cryptography can be traced back to ancient civilizations, such as the Egyptians and Greeks, who used simple substitution ciphers to protect messages. However, it wasn't until the Renaissance that cryptography began to evolve into a more sophisticated science. In the 16th century, a Venetian diplomat named Giovan Battista Bellaso introduced the concept of polyalphabetic ciphers, which used multiple alphabets to encrypt messages. Later, in the 20th century, the development of computers and the internet paved the way for the creation of modern cryptographic algorithms.
The Basic Principles Of Cryptography
At its core, cryptography is about transforming plaintext (the original message) into ciphertext (the encrypted message) using a secret key. The ciphertext can only be deciphered back into plaintext by someone who has access to the secret key. This ensures that only the intended recipient can read the message, and any unauthorised person who intercepts it cannot read it.
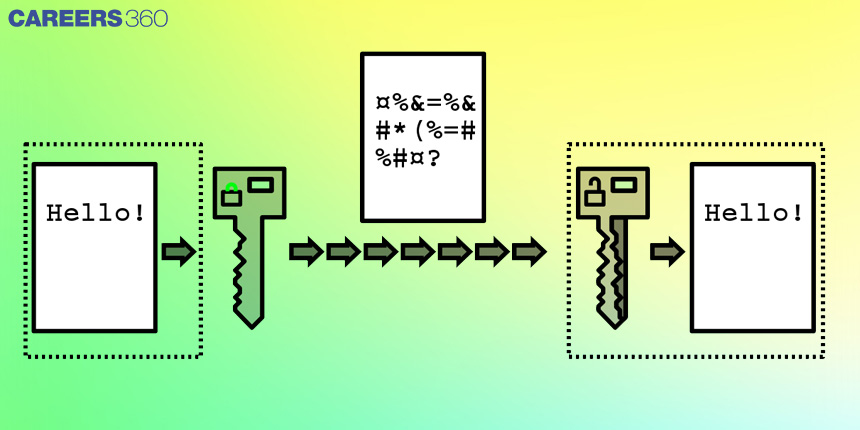
There are two main types of cryptography – symmetric and asymmetric. Symmetric cryptography uses the same key for encryption and decryption, while asymmetric cryptography uses two different keys: a public key for encryption and a private key for decryption. Asymmetric cryptography is generally considered more secure, as the private key is never shared, and therefore, cannot be intercepted.
The Role Of Mathematics In Cryptography
Mathematics is fundamental to cryptography. The use of mathematical concepts and algorithms is what enables the creation of secure cryptographic algorithms. For example, one of the most widely used cryptographic algorithms, the RSA algorithm, uses the concept of prime factorization.
The mathematics behind cryptography includes a variety of topics, such as number theory, modular arithmetic, and probability theory. Number theory, in particular, plays a crucial role in cryptography.
Number Theory
Number theory is a branch of mathematics that deals with the properties and relationships of numbers, particularly integers. It explores various topics such as prime numbers, divisibility, factorization, modular arithmetic, and more.
Modular Arithmetic
Modular arithmetic is a type of arithmetic that deals with the remainder when a number is divided by another number. It is used in cryptography to perform mathematical operations on large numbers that are too big to be processed efficiently by a computer. For example, in modular arithmetic, the expression 15 mod 7 (read as "15 modulo 7") means the remainder when 15 is divided by 7, which is 1.
Euclidean Algorithm
This algorithm is used to find the greatest common divisor (GCD) of two numbers. It plays an important role in the RSA algorithm, which relies on the difficulty of factoring large composite numbers.
Prime Numbers
Prime numbers are numbers that are only divisible by 1 and themselves. They are used extensively in cryptography because of their unique properties. For example, it is easy to multiply two large prime numbers together, but it is very difficult to factor the product back into its original prime factors. This property is used in public key cryptography algorithms like RSA.
RSA Algorithm
The algorithm works as follows:
Choose two prime numbers, p and q, such that p ≠ q. These will be the keys for the algorithm.
Compute n = pq. This is the modulus for the algorithm.
Compute φ(n) = (p-1)(q-1), where φ is Euler's totient function. This is used to generate the encryption and decryption keys.
Choose an integer e such that 1 < e < φ(n), and e is coprime to φ(n). This is the encryption key.
Compute d such that ed ≡ 1 (mod φ(n)), i.e., d is the multiplicative inverse of e modulo φ(n). This is the decryption key.
The encryption function takes a message M, and computes C = M^e (mod n). This is the ciphertext.
The decryption function takes a ciphertext C, and computes M = C^d (mod n). This is the original message.
Also check - Save Yourself From These Three Harmful Effects Of Poor Sleep
Let's walk through an example to see how this algorithm works.
Suppose we choose p = 5 and q = 11. Then n = pq = 55. We compute φ(n) = (5-1)(11-1) = 40.
We choose e = 3, which is coprime to 40. We can verify that 3 and 40 are coprime by checking that their greatest common divisor is 1.
We compute d such that 3d ≡ 1 (mod 40). This can be done using the extended Euclidean algorithm, which gives us d = 27.
Suppose we want to encrypt the message M = 9. We compute C = M^e (mod n) = 9^3 (mod 55) = 44. So the ciphertext is 44.
To decrypt the message, we compute M = C^d (mod n) = 44^27 (mod 55) = 9. So we have successfully decrypted the message.
This algorithm is based on the fact that it is computationally difficult to factor large integers into their prime factors. This means that an attacker who knows the modulus n, but not the prime factors p and q, cannot easily compute φ(n) and thus cannot determine the encryption and decryption keys. This makes the algorithm secure for use in practice.
There are several technologies that rely on encryption to ensure security and privacy. Here are a few examples:
Virtual Private Networks (VPNs): VPNs use encryption to create a secure and private connection between a user's device and a remote server. This ensures that any data sent over the connection is encrypted and cannot be intercepted by anyone who may be trying to eavesdrop.
Password Managers: Password managers use encryption to store and protect users' login credentials. This ensures that passwords cannot be accessed or stolen by unauthorized users.
Blockchain Technology:
Blockchain technology is a decentralised, distributed ledger that is used to record transactions across many computers in a secure and tamper-proof way. Each block in the chain contains a cryptographic hash of the previous block, a timestamp, and transaction data.
Blockchain relies heavily on encryption to ensure the security and integrity of the data it stores. The two main types of encryption used in blockchain are symmetric and asymmetric encryption.
Symmetric encryption is a type of encryption where the same key is used to both encrypt and decrypt the data. In the case of blockchain, this key is used to secure the data stored in each block. This ensures that the data is only accessible to those who have the key, preventing unauthorised access and tampering.
Asymmetric encryption, on the other hand, uses two keys: a public key and a private key. The public key is used to encrypt the data, while the private key is used to decrypt it. This type of encryption is often used in blockchain to verify transactions and ensure that they are legitimate.
In modern times, blockchain technology has become increasingly prevalent in a variety of fields, spanning from cryptocurrencies and supply chain management to voting systems and smart contracts, among others.
Challenges Of Cryptography
While cryptography has come a long way since the days of simple substitution ciphers, it still faces several challenges. One of the biggest challenges is the threat of quantum computing. Quantum computers have the potential to break many of the encryption algorithms used today, as they can perform calculations at a much faster rate than traditional computers. As a result, cryptographers are constantly working on developing new cryptographic algorithms that are resistant to quantum computing.
Another challenge facing cryptography is the threat of cyber attacks. While cryptographic algorithms are designed to be secure, they can still be vulnerable to attacks. For example, a brute-force attack involves trying every possible key until the correct one is found. This is why key length is so important in cryptography; the longer the key, the more difficult it is to crack.
Also check - Understand The Science Behind Nuclear Weapons