BODMAS Full Form
Introduction
At first glance, it appears that “BODMAS” is an acronym. This is, indeed, correct. You will learn here the full form of “BODMAS” and also its functionality.
As such, you are aware of the mathematical operations- “addition”, “subtraction”, “multiplication”, and “division”. These mathematical operations are represented with their respective “mathematical operators” in any mathematical expression. Isn’t it right? Apart from these common “mathematical operators”, you will also see the occurrence of symbols like “{}”, “()”, etc., the indices of numbers (e.g. \[{{2}^{2}},\ {{55}^{-6}}\] ![]() ), and the powers of variables (e.g. \[{{x}^{3}},\ {{y}^{-5}}\]
), and the powers of variables (e.g. \[{{x}^{3}},\ {{y}^{-5}}\] ![]() ). Let us dive into it to explore further.
). Let us dive into it to explore further.
- What is the full form of “BODMAS”?
- What Are “BODMAS RULES“?
- How Many Types Of “Brackets” Are There In The “BODMAS Rules”?
- What Is “Index Power”?
- What Are The Four “Arithmetic Operators” In The “BODMAS Rules”?
- What is the importance of “BODMAS”?
What is the full form of “BODMAS”?
The word “BODMAS” is such an abbreviation, where every constituent letter indicates the initial letters of the “mathematical operators”, as described below.
The first letter “B” stands for “Brackets”,
The second letter “O” stands for “Order”,
The third letter “D” stands for “Division”,
The fourth letter “M” stands for “Multiplication”,
The fifth letter “A” stands for “Addition”, and
The last letter “S” stands for “Subtraction”.
What Are “BODMAS RULES“?
Look at this mathematical expression.
\[6000\div \left( {{2}^{4}}\times 3 \right)+{{5}^{3}}-63\]
![]()
Note that this above mathematical expression involves some numbers [like “6000”, 63, etc.], and certain “mathematical operators”, [like “+”, “X”, etc.].
It is definite that the “mathematical operators”, here denote corresponding “mathematical operations”.
Also, you can see the exponents [like “4” in “24”].
So, where will you start to calculate this mathematical expression? Will you prefer to start from “the Right Hand Side” or the “Left Hand Side”? Wait!
Basically, to evaluate any “mathematical expression”, there are universal rules to decide “which mathematical operation will come first, and which mathematical operation will follow it, sequentially”.
To remember these subsequent preferences of “mathematical operations”, a mnemonic is formed with the respective initial letters of the successive “mathematical operators” which is named “BODMAS Rules”.
Thus, the “BODMAS Rules” dictate the preferences of the individual “mathematical operators” in any mathematical expression.
How Many Types Of “Brackets” Are There In The “BODMAS Rules”?
For “Brackets”, you have the first letter “B” in the abbreviation “BODMAS”. Note that there are the following types of brackets.
“First Brackets” or “Parentheses”
You can identify the “First Brackets” or “Parentheses” with the symbol “()”, e.g. \[90\div \left( {{2}^{4}}\times 3 \right)+{{5}^{3}}-63\] ![]()
“Second Brackets” or “Curly Brackets”
You can recognize the “Second Brackets” or “Curly Brackets” with the symbol “{}”, e.g. \[90\div \left\{ \left( {{2}^{4}}\times 3 \right)+{{5}^{3}} \right\}-63\] ![]()
“Third Brackets” of “Square Brackets”
You can find the “Third Brackets” of “Square Brackets” with the symbol “[ ]”, e.g. \[90\div \left[ \left\{ \left( {{2}^{4}}\times 3 \right)+{{5}^{3}} \right\}-63 \right]\] ![]()
What Is “Index Power”?
In the mathematical terms, you may have noticed some terms are present as “superscripts” [like “14” in “1214”]. These “superscripts” are nothing but the “powers” of its immediate attached term (or “base”) and, are known as the “exponents” or the “indices” of the associated “base” [like “12” is the base of the “1214”]. This is what is referred to as “Order” and is indicated by the second letter “O” in the “BODMAS Rules”.
Note that the “Order” indicated by the second letter “O” in the “BODMAS Rules” can be an “integer”, “rational number”, irrational number, or even “complex number”.
What Are The Four “Arithmetic Operators” In The “BODMAS Rules”?
The “BODMAS Rules” covers the following four “arithmetic operations”.
Division
The mathematical operation where you divide any number or “mathematical term” with another one is termed “division”.
The symbol that is used to denote “division” is “/” or “![]() ”, and it is known as the “division operator” or “divide” sign, e.g. \[890\div \left( {{2}^{4}}\div 3 \right)+5/63\]
”, and it is known as the “division operator” or “divide” sign, e.g. \[890\div \left( {{2}^{4}}\div 3 \right)+5/63\] ![]()
Multiplication
The mathematical operation where you multiply any number or “mathematical term” with another one is termed “multiplication”.
The symbol that is applied to indicate “multiplication” is “*” or “![]() ”, and it is known as the “multiplication operator” or “multiply” sign, e.g. \[890\times \left( {{2}^{4}}\times 3 \right)+5*63\]
”, and it is known as the “multiplication operator” or “multiply” sign, e.g. \[890\times \left( {{2}^{4}}\times 3 \right)+5*63\] ![]()
Addition
The mathematical operation where you add any number or “mathematical term” with another one is termed “addition”.
The symbol that is used to denote “addition” is “+”, and it is known as the “addition operator” or “plus” sign, e.g. \[890+\left( {{2}^{4}}+3 \right)\times 5+63\] ![]()
Subtraction
The mathematical operation where you subtract any number or “mathematical term” with another one is termed “subtraction”.
The symbol that is used to denote “subtraction” is “-”, and it is known as the “subtraction operator” or “minus” sign, e.g. \[890-\left( {{2}^{4}}-3 \right)+5-63\] ![]()
What is the importance of “BODMAS”?
You can easily realize the importance of “BODMAS” if you compare the following two cases to solve the problem \[855\div \left( {{2}^{4}}+3 \right)\times 5+96\div 8\times 7-3=?\] ![]()
CASE-1: “BODMAS” not applied to
Perform this calculation from the right-hand side, without applying “BODMAS”.
\[\begin{align}
855\div \left( {{2}^{4}}+3 \right)\times 5+96\div 8\times 7-3 \\
=855\div \left( {{2}^{4}}+3 \right)\times 5+96\div 8\times 4 \\
=855\div \left( {{2}^{4}}+3 \right)\times 5+96\div 32 \\
=855\div \left( {{2}^{4}}+3 \right)\times 5+3 \\
=855\div \left( {{2}^{4}}+3 \right)\times 8 \\
=855\div \left( {{2}^{4}}+3 \right)\times 8 \\
=855\div \left( {{2}^{4}}\times 8+3\times 8 \right) \\
=855\div \left( 128+24 \right) \\
=855\div 152 \\
=5.625(\text{wrong answer)} \\
\end{align}\]
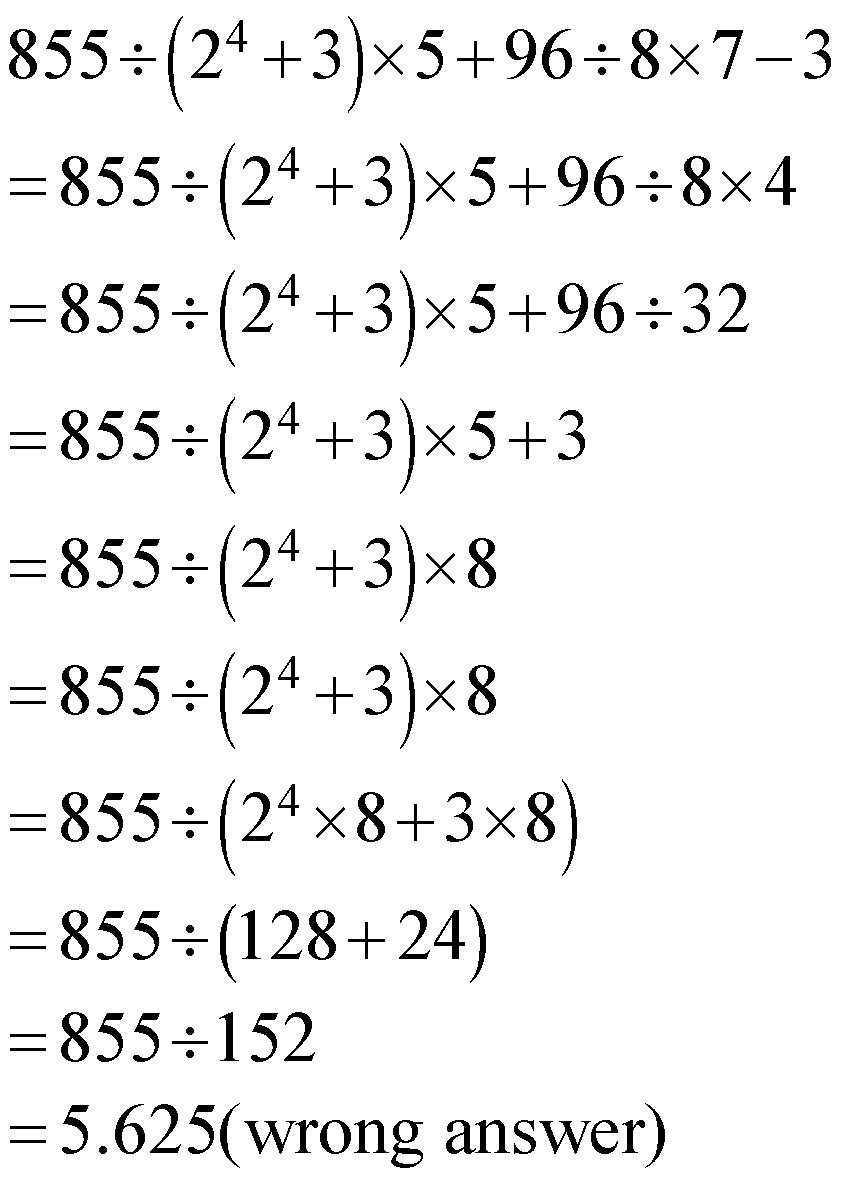
CASE-2: “BODMAS” applied to
Perform this calculation by applying “BODMAS”.
\[\begin{align}
855\div \left( {{2}^{4}}+3 \right)\times 5+96\div 8\times 7-3 \\
=855\div \left( 16+3 \right)\times 5+96\div 8\times 7-3 \\
=855\div 19\times 5+96\div 8\times 7-3 \\
=45\times 5+12\times 7-3 \\
=225+84-3 \\
=309-3 \\
=306\text{ (Right Answer)} \\
\end{align}\]
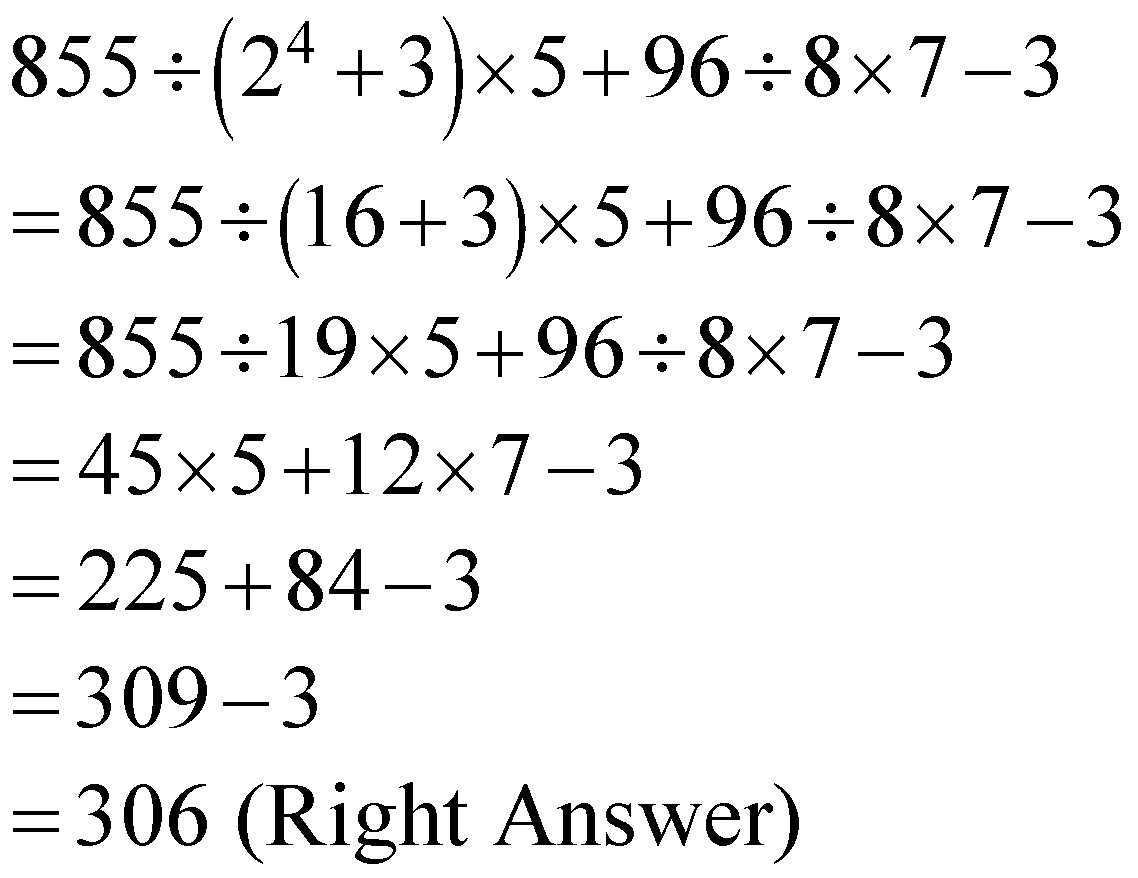
Every mathematical expression yields the universally accepted “correct result”, only when you follow these “BODMAS Rules”.