BPT Theorem Full Form

What is the full form of BPT Theorem?

BPT theorem stands for Basic Proportionality Theorem. The basic proportionality theorem was put out by the great Greek mathematician Thales. The renowned mathematician stated that the ratio of any two corresponding sides of any two equiangular triangles is always equal. The basic proportionality theorem (BPT) was put forth in accordance with this idea. It reveals how any two equiangular triangles' sides relate to one another. Similar triangles have introduced the Thales theorem notion. If the two triangles shown are similar to one another, then

• Both triangles' corresponding angles are the same.

• Both triangles' corresponding sides are proportionate to one another.

Thus, the theorem also aids in our understanding of the notion of similar triangles.

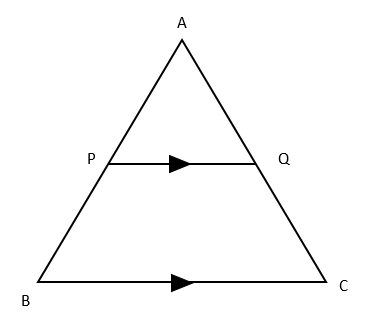
The theorem states that "the other two sides of a triangle are divided in the same ratio if a line drawn parallel to one side of a triangle intersects the other two sides at distinct spots." For instance, line PQ is drawn parallel to side BC in the example picture such that it connects the other two sides, AB and AC. It can be inferred from the fundamental proportionality principle that \mathbf{AP}/\mathbf{PB}=\mathbf{AQ}/\mathbf{QC}\

BPT Theorem Proof

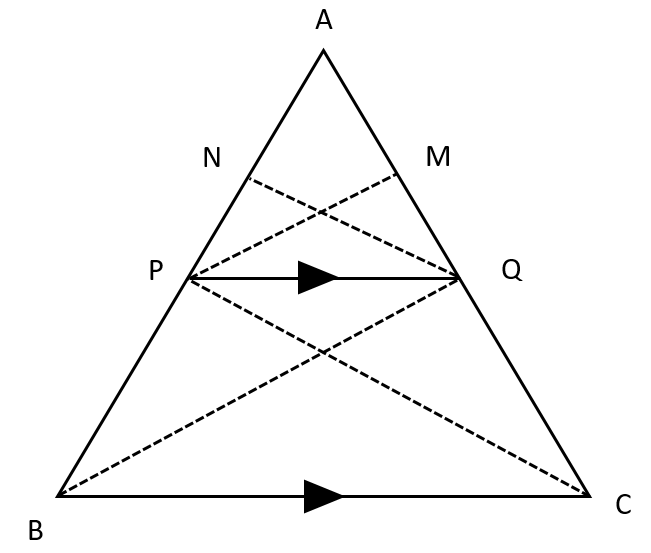
Considering triangles APQ and BPQ. Both have the same height which is QN.

Therefore,

area\text{ }of\text{ }\Delta APQ=\frac{1}{2}\times AP\times QN\

And also,

area\text{ }of\text{ }\Delta PBQ=\frac{1}{2}\times PB\times QN\

Considering triangles APQ and QCP. Both have the same height which is PM.

Therefore,

area\text{ }of\text{ }\Delta APQ=\frac{1}{2}\times AQ\times PM\

And also,

area\text{ }of\text{ }\Delta QCP=\frac{1}{2}\times QC\times PM\

..............(1)

Now,

\frac{area\text{ }of\text{ }\Delta APQ}{area\text{ }of\text{ }\Delta PBQ}=\frac{\frac{1}{2}\times AP\times QN}{\frac{1}{2}\times PB\times QN}=\frac{AP}{PB}\

In the same way,

\frac{area\text{ }of\text{ }\Delta APQ}{area\text{ }of\text{ }\Delta QPC}=\frac{\frac{1}{2}\times AQ\times PM}{\frac{1}{2}\times QC\times PM}=\frac{AQ}{QC}\

..................(2)

According to the property of triangles, Triangles drawn on the same base and within the same set of parallel lines have equal areas.

Thus,

area\text{ }of\text{ }\Delta PBQ=area\text{ }of\text{ }\Delta QCP\

........................(3)

Now from equations (1), (2), and (3), we get:

\mathbf{AP}/\mathbf{PB}=\mathbf{AQ}/\mathbf{QC}\

Hence Proved.