Boyles Law - History, Formula, Examples, Exercises, FAQs
Have you ever wondered why a balloon shrinks when you squeeze it, or why breathing feels different at high altitudes? What happens to the volume of a gas when the pressure on it is increased? You will find these answers by reading this article on Boyle's law. Boyle's law states that pressure exerted by the gas is inversely proportional to the volume occupied by the (of a given mass, kept at a constant temperature) gas. As long as the temperature and amount of gas are constant, the pressure and volume of a gas are inversely proportional. A law, Boyle’s law formulated by Robert Boyle in the year 1662, states that under certain conditions, the solution is unstable.
This Story also Contains
- Boyle's law
- Relation between Density and Pressure
- Boyle’s law Formulas and Their Derivations
- Boyle’s law Example
- Some Solved Examples
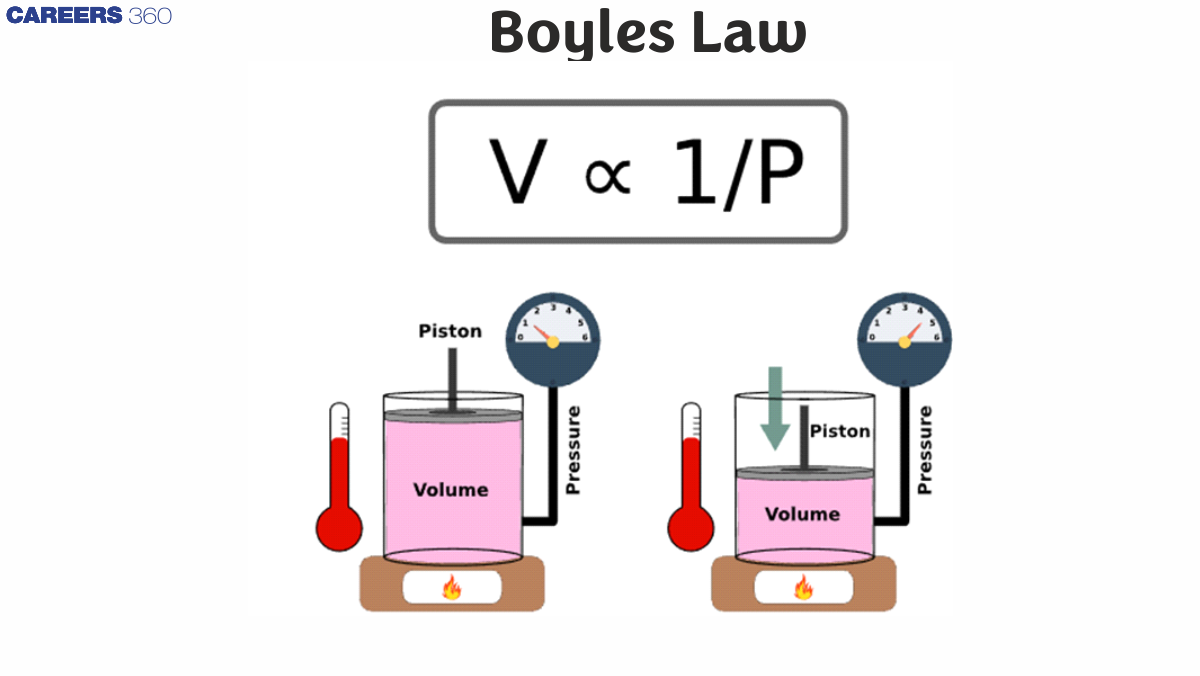
Boyle's law
Boyle’s Law states that for a fixed amount of gas at constant temperature, the pressure of the gas is inversely proportional to its volume.
Assuming constant mass and temperature, volume and pressure are proportional (at constant volume).
P ∝ (1/V)
A gas exerts pressure and occupies volume according to the equation PV. A constant, k, can be added to this proportionality to convert it into an equation.
$P=k^*(1 / V) \Rightarrow P V=k$
The Boyle's law may be expressed mathematically as
$\mathrm{P} \propto \frac{1}{\mathrm{~V}},($ at constant T and n$)$
or $\mathrm{V} \propto \frac{1}{\mathrm{P}},($ at constant T and n$)$
Where,
$\mathrm{T}=$ temperature, $\mathrm{P}=$ pressure of the gas
$\mathrm{n}=$ number of moles of a gas and $\mathrm{V}=$ volume of the gas
$
\Rightarrow \mathrm{V}=\mathrm{k}_1 \frac{1}{\mathrm{P}}
$
k1 is the proportionality constant whose value depends upon the following factors.
- Amount of gas
- Temperature
On rearranging the above equation we can write
$\mathrm{PV}=\mathrm{k}_1$
i.e., 'PV' is constant at constant temperature and for a fixed amount of the gas. So, Boyle's law can also be stated as "At constant temperature, the product of pressure and volume of a fixed amount of a gas remains constant."
Now if the initial pressure and volume of a fixed amount of gas at constant temperature are P1 and V1, and after expansion, the new pressure of the gas is P2 and volume occupied is V2 then according to Boyle's law
$\begin{aligned} & \mathrm{P}_1 \mathrm{~V}_1=\mathrm{P}_2 \mathrm{~V}_2=\text { constant } \\ & \text { or } \frac{P_1}{P_2}=\frac{V_2}{V_1}\end{aligned}$
Relation between Density and Pressure
According to Boyle's law at constant temperature and constant mass
$V \propto \frac{1}{P}$, As T and mass are constant
$V \propto \frac{1}{d}$, Here d is the density
As $\mathrm{V}=$ Mass/density
so $\quad \frac{1}{d} \propto \frac{1}{P}$
that is, $\mathrm{d} \propto P$ or $\mathrm{d}=\mathrm{K} / \mathrm{P}$
or $\log _{10} P=\log _{10} 1 / V+\log _{10} K$
$d_1 / P_1=d_2 / P_2$
Also read :
Boyle’s law Formulas and Their Derivations
The pressure exerted by a gas changes with the change in its volume (at constant volume and temperature). This is Boyle's law. Hence, the initial pressure of a gas will equal the initial volume of a gas when its final pressure and volume are constant (at constant temperature and mole number). Mathematically, the law can be expressed as follows:
P1V1 = P2V2
Where,
Initially, the gas exerts a pressure of P1
V1 is the volume in which the gas is initially present.
Ultimately, the gas exerts a pressure of P2
V2 represents the final volume occupied by the gas
In Boyle’s law, we can get this expression from the pressure-volume relationship. In a constant-temperature environment, PV is equal to k when a fixed volume of gas is present. Consequently,
P1V1 = k (pressure * volume at the start)
P2V2 = k (temperature * volume)
∴ P1V1 = P2V2
When the volume of a gas's container is reduced (and its quantity and absolute temperature remain unchanged), this equation can be used to predict the increase in pressure exerted by the gas on its walls.
|
Related Topics |
Boyle’s law Example
A balloon filled with air reduces in volume when squeezed. The increase in air pressure is accompanied by an increase in the pressure exerted by the air on the balloon, according to Boyle’s law. A balloon that is squeezed further eventually pops due to increasing pressure. Here is an illustration that illustrates the increase in pressure associated with a decrease in the volume of a gas.
Scuba divers may experience gas molecules in their bodies expanding if they rapidly ascend from a deep zone to the surface. The gas bubbles can cause organ damage and even death to the diver. Another example of Boyle’s law is the expansion of the gas caused by the scuba diver's ascent. Similarly, dissolved gasses in fish blood can expand when they reach the surface of the water (due to their exposure to heightened temperatures).
Some Solved Examples
Question 1: What is the value of $-\frac{1}{V}\left(\frac{d V}{d p}\right)_{T, n}$ at 0.2 ban?
1) 6 bap $^{-1}$
2) abarb ${ }^{-1}$
3) (correct) $5 \mathrm{bar}^{-1}$
4) $4 \operatorname{bar}^{-1}$
Solution:
This is a case of Boyle's law under isothermal conditions.
$\begin{aligned}
& \mathrm{V} \alpha \frac{1}{\mathrm{p}} \Rightarrow \mathrm{~V}=\frac{\mathrm{k}}{\mathrm{p}} \\
& \therefore\left(\frac{\mathrm{dV}}{\mathrm{dp}}\right)=-\frac{\mathrm{k}}{\mathrm{p}^2}=\frac{-\mathrm{pv}}{\mathrm{p}^2}=\frac{-\mathrm{V}}{\mathrm{p}} \\
& \therefore-\frac{1}{\mathrm{~V}}\left(\frac{\mathrm{dV}}{\mathrm{dp}}\right)=-\frac{1}{\mathrm{p}}=\frac{1}{0.2}=5 \mathrm{bar}^{-1}
\end{aligned}$
Hence, the answer is option (3).
Question 2: The combination of plots which does not represent isothermal expansion of an ideal gas is -

1) A and C
2) B and C
3) (correct) B and D
4) A and D
Solution:
In isothermal expansion, $P V_{\mathrm{m}}=\mathrm{k}$ (constant). This relation is plotted in graph' c '.
likewise, $\mathrm{P}=\frac{\mathrm{k}}{\mathrm{V}_{\mathrm{m}}}$
This relation is plotted in graph ' A '.
Thus, graphs B and D are incorrect.
Hence, the answer is option (3).
Question 3: Global warming is due to an increase of:
1) methane and nitrous oxide in the atmosphere
2) (correct) methane and CO2 in the atmosphere
3) methane and O3 in the atmosphere
4) methane and CO in the atmosphere
Solution:
Global warming is caused by greenhouse gases like CO2, methane, etc.
Hence, the answer is option (2).
Question 4: At constant temperature, in a given mass of ideal gas -
1) The ratio of pressure and volume always remains constant
2) Volume always remains constant
3) Pressure always remains constant
4) (correct) The product of pressure and volume always remains constant
Solution:
According to Boyle's law, at constant temperature and moles, Pressure is inversely proportional to the volume of gas. $P_1 V_1=P_2 V_2$ i.e $\mathrm{PV}=$ Constant
Hence, the answer is option (4).
Practice More Questions With The Link Given Below:
Also check-
| NCERT Exemplar Class 11th Chemistry Solutions | |
| NCERT notes Class 12 Chemistry | NCERT Exemplar Class 12th Chemistry Solutions |
| NCERT Notes For All Subjects | NCERT Exemplar Solutions for All Subjects |
Frequently Asked Questions (FAQs)
If the volume of a gas decreases while its temperature remains constant, its pressure will increase. Conversely, if the volume increases, the pressure will decrease. This relationship is a key aspect of Boyle's Law.
An inverse relation between pressure and volume is Boyle’s law of gases. A constant temperature leads to increased volume and a falling pressure when a constant temperature is maintained.
The significance of Boyle’s law lies in the way gas behaves. This proves that the pressure and volume of a gas are inversely related. The volume shrinks as the pressure rises when you apply pressure to a gas.
According to Boyle's empirical law, the pressure (p) will change inversely with the volume (v) of a given quantity of gas at constant temperature; i.e., PV = k, a constant.
In practice, Boyle’s law can be applied to a balloon. When you blow air into a balloon, it expands as the pressure pulling on the rubber causes it to expand. A balloon's un-squeezed section expands outward when a compressed end is compressed, causing its pressure to rise.
Pressure and volume are connected by Boyle’s law. In inverse proportion to the volume of a gas, the pressure will increase at a constant temperature. Empirical proof of the law is possible. It presents an experimental approach that uses syringes to verify the law.