Charles’ Law

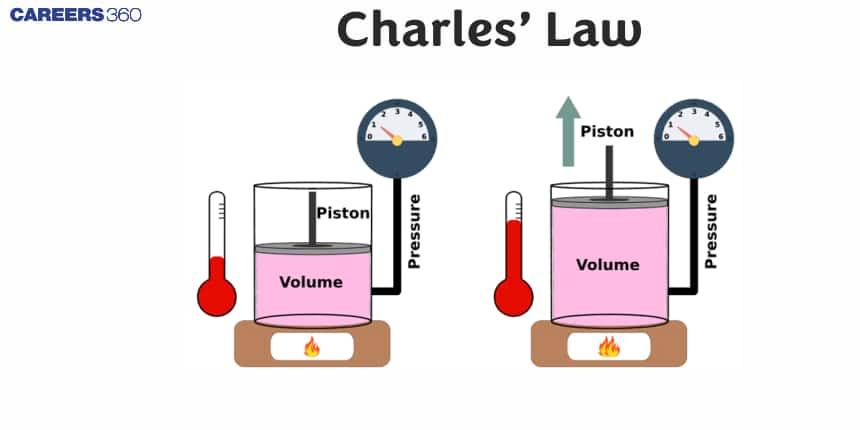
Charles' Law is one of the basic laws related to gases, which talks about the relationship between the volume and temperature of a gas at constant pressure. The law is known as Charles's Law, named after Jacques Charles. It states that the volume of a given amount of gas is directly proportional to its temperature when measured in Kelvin—provided, i.e., the pressure is constant. In other words, if the temperature of a gas is increased, its volume is also increased, whereas if the former is lowered, the latter is also lowered.

This Story also Contains

1. Charles' Law
2. Some Solved Examples
3. Summary

Charles' Law

In order to explain it, let us consider the following plot between volume and temperature.

It shows that the volume of a definite amount of a gas varies linearly with temperature on Celsius scale. It can be given as:
V_t = a + bt
Here a and b are constants. $\begin{aligned} & \mathrm{a}=\mathrm{V}_0 \text { at } 0^{\circ} \mathrm{C} \\ & \mathrm{b}=\operatorname{slope}(\partial \mathrm{V} / \partial \mathrm{T})_{\mathrm{P}}\end{aligned}$

So according to Charle's law, "At constant pressure, the volume of a given mass of a gas increases or decreases by 1/273 of its volume at 0^oC for every one degree centigrade rise or fall in temperature" that is,

$
\begin{aligned}
& V_1=V_0+\frac{V_0}{273} \times t^{\circ} \mathrm{C} \text { (at const. temp.) } \\
& =V_0\left(1+t^{\circ} \mathrm{C} / 273\right)=V_0\left(273+t^{\circ} \mathrm{C} / 273\right) \\
& =V_0 \frac{\mathrm{T}}{273}
\end{aligned}
$

Therefore
$\mathrm{V}_{\mathrm{t}} \propto \mathrm{T}$ or $\mathrm{V} \propto \mathrm{T}$ at constant pressure i.e.,
Or $\mathrm{V} / \mathrm{T}=$ constant
Hence "At constant pressure, the volume of a given mass of a gas is directly proportional to its temperature in Kelvin."$\frac{\mathrm{V}_1}{\mathrm{~T}_1}=\frac{\mathrm{V}_2}{\mathrm{~T}_2}$ At constant pressure

Relation between Density and Temperature

$\begin{aligned} & \text { As } \mathrm{V} \propto 1 / d,(\mathrm{~d}=\text { density }) \text {, So } \\ & V \propto T \\ & \text { So } \mathrm{d} \times \mathrm{T}=\text { constant } \\ & \text { that is, } d_1 T_1=d_2 T_2\end{aligned}$

Absolute Scale of Temperature or Absolute Zero
According to Charle's law, we have:

$V_0\left(1+t^o C / 273\right)$

If the temperature of a gas is lowered up to - 273^oC the volume of the gas becomes zero. This temperature is known as absolute zero and this zero point on the scale is called as Kelvin scale.

The absolute value of this temperature is - 273^oC. At this temperature, the pressure, kinetic energy, and heat content Of the gas is also zero. Absolute zero does not indicate thus zero value of the volume of the gas is the indicator. There is no significance of gas laws at this temperature as the gas phase is not observed here as a gas liquefied or solidified before this temperature.

When a graph is plotted between the volume of the gas against this temperature at constant pressure, it is called isobar and it is always a straight line.

Plots between V vs T

(i) A straight-line graph is obtained.

(ii) The slope of lines obtained at different temperatures is different

(iii) The temperature circled is absolute zero temperature (0 K or -273.15^oC) where is 0 K and all the lines meet.

Isobars: The curves of volume temperature graphs at different fixed pressures are called isobars.

All gases obey Charles Law at low pressures and high temperatures.

Physical Significance of Charles' Law:

Hot air balloon technology is based on Charles Law. On an increase in temperature, air expands. So, the density of air decreases. The hot air in the balloon is less dense and lighter than the atmospheric air. Therefore the balloons filled with hot air rise up for meteorological observations.

Recommended topic video on (Charles' Law)

Some Solved Examples

Example 1: At 100^oC a gas has 1 atm pressure and 10 L volume. Its volume at STP would be -

1)10 L

2) Less than 10 L

3)More than 10 L

4)None of these

Solution

Charles’s Law -

At constant pressure and moles, the volume is directly proportional to the temperature of the gas.

$\begin{aligned} & \frac{V_1}{T_1}=\frac{V_2}{T_2} \\ & T_1=373 K, \quad T_2=273 K \\ & V_1=10 L, \quad V_2=? \\ & \frac{V_1}{T_1}=\frac{V_2}{T_2}, \quad \frac{10}{373}=\frac{V_2}{273} \\ & V_2=7.32 L\end{aligned}$

It is less than 10L.

Hence, the answer is the option (2).

Example 2: At $100^{\circ} \mathrm{C}$ a gas has 1 atm pressure and 10 L volume. Its volume (in L) at NTP would be -

1)10.9

2) 7.8

3)15.3

4)12.14

Solution

Given,

At 100^oC,P=1atm

V=10L

At NTP, T₂ = 20^oC

P=1atm

So, the Temperature in Kelvin,

$\begin{aligned} & \mathrm{T}_1=373.15 \mathrm{~K}, \mathrm{~T}_2=293.15 \mathrm{~K} \\ & V_1=10, V_2=? \\ & \frac{V_1}{T_1}=\frac{V_2}{T_2} \Rightarrow \frac{10}{373}=\frac{V_2}{293}\end{aligned}$

$V_2=7.8$ i.e less than 10L

Hence, the answer is the option (2).

Example 3: On a ship sailing in the Pacific Ocean where the temperature is $23.4^{\circ} \mathrm{C}$, a balloon is filled with 2L air. What will be the volume (in L) of the balloon when the ship reaches the Indian Ocean where the temperature is $26.1^{\circ} \mathrm{C}$?

1)1.56

2)2.56

3)1.87

4) 2.01

Solution

According to Charles’ law, we have:

$\frac{V_1}{T_1}=\frac{V_2}{T_2}$

Now, we have given:
V₁ = 2L
T₁= 273 + 23.4 = 296.4K
T₂ = 273 + 26.1 = 299.1K

Thus:

$\begin{aligned} \mathrm{V}_2 & =\frac{\mathrm{V}_1 \times \mathrm{T}_2}{\mathrm{~T}_1} \\ \mathrm{~V}_2 & =\frac{2 \times 299.1}{296.4}=2.01 \mathrm{~L}\end{aligned}$

Hence, the answer is the option (4).

Example 4:Calculate the % increase in the temperature of gas when it is heated at constant pressure to occupy a 20% increase in volume.

1)30

2)15

3) 20

4)25

Solution

We have:

$\begin{aligned} & \mathrm{V}_2=\mathrm{V}+\frac{20 \mathrm{~V}}{100}=\frac{120 \mathrm{~V}}{100} \\ & T=T_2\end{aligned}$

$T=T_2$

From Charles’ law, we know:

$\begin{aligned} & \frac{\mathrm{V}_1}{\mathrm{~T}_1}=\frac{\mathrm{V}_2}{\mathrm{~T}_2} \\ & \therefore \mathrm{T}_2=\frac{120 \mathrm{~V} \times \mathrm{T}_1}{100 \times \mathrm{V}}=1.2 \mathrm{~T}_1\end{aligned}$

Thus, an increase in temperature $=1.2 T_1-T_1=0.2 T_1$

Therefore, % increase in temperature $=\left(0.2 T_1 / T_1\right) \times 100=20 \%$

Alternate Solution:

Vol ${ }^m$ Initial $=V$
Increase in $\mathrm{vol}^m=V+V \times \frac{20}{100}=1.2 \mathrm{~V}$

$\begin{aligned} & \because \text { At constant pressure } \\ & \frac{V_1}{T_1}=\frac{V_2}{T_2} \\ & \Rightarrow \frac{\mathrm{V}}{\mathrm{T}_1}=\frac{1.2 \mathrm{~V}}{\mathrm{~T}_2} \\ & \Rightarrow \frac{\mathrm{T}_2}{\mathrm{~T}_1}=1.2 \\ & \Rightarrow \frac{\mathrm{T}_2}{\mathrm{~T}_1}-1=1.2-1=0.2 \\ & \Rightarrow \frac{\mathrm{T}_2-\mathrm{T}_1}{\mathrm{~T}_1} \times 100=20 \%\end{aligned}$

Hence, the answer is the option (3).

Example 5: A bulb of three-litre capacity filled with air is heated from $27^{\circ} \mathrm{C}$ to $t^{\circ} \mathrm{C}$. The air thus expelled measured 1.45L at $17^{\circ} \mathrm{C}$. Considering the pressure to be 1 atm throughout the experiment and ignoring the expansion of the bulb, calculate the temperature (in ^oC).

1) 327

2)320

3)350

4)335

Solution

We have:
The initial volume of bulb = 3L
Initial temperature = 273 + 27 = 300K
Final temperature = 273 + t
Thus, according to Charles’ law, we have:

$\frac{V_1}{T_1}=\frac{V_2}{T_2}$

Now, the volume of gas is 1.45L, thus, we have:

$\frac{1.45}{290}=\frac{V}{t+273}$...............................(i)

Now the gas is heated from $27^{\circ} \mathrm{C}$ to, the volume can be given as follows:

$\frac{3}{300}=\frac{3+V}{273+V}=\frac{V}{273+t}+\frac{3}{273+t}$

Using equation (i) we have:

$\frac{3}{300}=\frac{3+V}{273+V}=\frac{1.45}{290}+\frac{3}{273+t}$

Thus, $t=327^{\circ} \mathrm{C}$

Hence, the answer is the option (1).

Summary

Charles' Law is an important concept in gas responses to temperature change. It explains many practical happenings, such as rising temperatures in hot air balloons and increased pressure on car tires on hot days. The law is indispensable in scientific and industrial contexts for aiding in the designing and operation of equipment by the behavior of gases. The importance of Charles' Law also reaches to other aspects, which bind many gas laws together, composing the ideal gas law. This principle itself integrates all key principles to cover gas behavior thoroughly. Charles' Law helps to explain the extent to which temperature influences gas volume and to predict the change in gas behavior