Concentration cell

The German chemist Heinrich Gustav Magnus discovered the concentration cell in 1837. Magnus was working on electrochemical cells and observed that a cell could be created from two half-cells containing the same electrodes but different concentrations of an electrolyte solution. The key finding was that the cell generated an electromotive force (EMF) due to the concentration difference of the electrolyte, even though the electrodes were identical. This discovery demonstrated that the electrical potential difference in such a cell arises from the difference in concentration of the electrolyte solutions, not from a difference in electrode materials.

This Story also Contains

1. Concentration Cell
2. Some Solved Examples
3. Summary

Magnus's work in this area led to a deeper understanding of how concentration gradients can drive electrical currents, which is fundamental to many electrochemical processes. Before Magnus, the field of electrochemistry was developing rapidly. Scientists like Alessandro Volta and John Frederic Daniell had already established the principles of galvanic cells and electrochemical reactions. Heinrich Gustav Magnus was experimenting with cells consisting of two half-cells with identical electrodes but different concentrations of the same electrolyte.

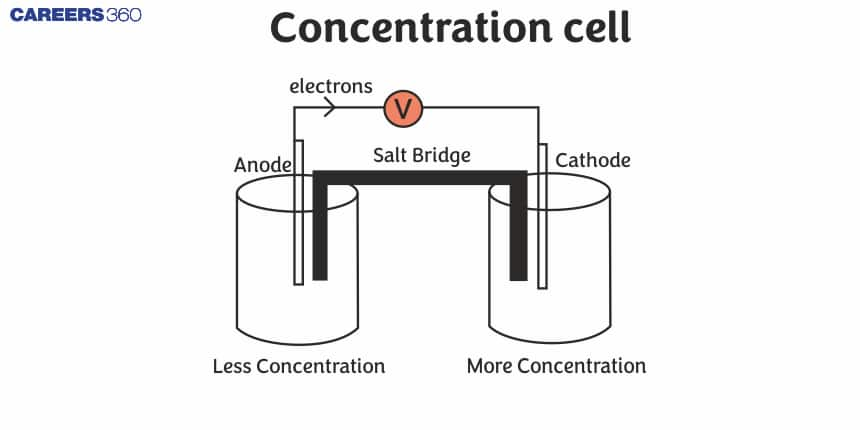
Concentration Cell

A concentration cell is a type of electrochemical cell where the electrodes are identical, but the electrolyte solutions in the two half-cells have different concentrations. The fundamental principle behind a concentration cell is that the electromotive force (EMF) is generated due to the difference in concentration of the electrolyte, rather than differences in electrode materials.

Key Components of a Concentration Cell:

Electrodes:

• The electrodes in a concentration cell are typically made from the same material, such as platinum or copper. Since they are identical, the difference in cell potential arises solely from the concentration difference in the electrolyte solutions.

Electrolyte Solutions:

• The cell consists of two half-cells, each containing a solution of the same electrolyte but at different concentrations. For example, one half-cell might contain a 0.1 M solution of copper sulfate (CuSO₄), while the other contains a 1.0 M solution of copper sulfate.

Salt Bridge:

• A salt bridge or a porous barrier is used to maintain electrical neutrality by allowing the flow of ions between the two half-cells. It completes the circuit and allows ions to migrate to balance the charge.

The device in which both the half cells contain the same electrode but differ in the concentration (or activity ) of the species involved. Oxidation and reduction occur at respective electrodes until the concentration becomes equal in both the half cells. In other words, the concentration cell is one in which emf arises as a result of different concentrations of the same electrolyte in the component half-cells.

• The two solutions are connected by a salt bridge and the electrodes are joined by a piece of metallic wire.
• A concentration cell dilutes the concentrated solution concentrates the more dilute solution and generates potential till the cell reaches an equilibrium.
• The potential is generated due to a decrease in Gibb's energy of the cell till the attainment of equilibrium.
• E^o of a concentration cell is equal to zero where the E_cell depends upon the concentration (on the acting of species involved).

Let us consider the given concentration cell,

\begin{tabular}{c|ccc|c}
$C u(s)$ & $C u^{2+}$ & $\|$ & $C u^{2+}(a q)$. & $C u(s)$ \\
& $C_1 M$ & $C_2 M$ &

For the above cell to be working, E_cell > 0

Therefore, From Nernst Equation:

$\begin{aligned} & \mathrm{E}_{\text {cell }}=\mathrm{E}_{\text {cell }}^{\mathrm{o}}-\frac{0.059}{2} \log \frac{\mathrm{c}_1}{\mathrm{c}_2} \\ & \mathrm{E}_{\text {cell }}=\mathrm{E}_{\text {cell }}^{\mathrm{o}}-\frac{0.059}{2} \log \frac{\mathrm{c}_1}{\mathrm{c}_2} \\ & \mathrm{E}_{\text {cell }}=0+\frac{0.059}{2} \log \frac{\mathrm{c}_2}{\mathrm{c}_1}>0 \\ & \Rightarrow \mathrm{c}_2>\mathrm{c}_1\end{aligned}$

Recommended topic video on (Concentration Cell)

Some Solved Examples

Example.1

1. Choose the correct option :

a) A concentration cell generates electricity from the reduction in the thermodynamics free energy.

b) Concentration cell has two half-cells having the same electrodes, differing only in concentration (or acting).

c) $E_{\text {cell }}^0=0$ in the case of a concentration cell.

1)a,c

2) (correct)a,b,c

3)a,b

4)b,c

Solution

All given statements are correct for a concentration cell.

Hence, the answer is the option (2).

Example.2

2. For the given cell; $C u(s) C u^{2+}\left(C_1 M\right) \| C u^{2+}\left(C_2 M\right) \mid C u(s)$ change in Gibbs energy $(\Delta G)$ is negative, if :

1)$C_1=C_2$

2)$C_2=\frac{C_1}{\sqrt{2}}$

3)$C_1=2 C_2$

4) (correct)$C_2=\sqrt{2} C_1$

Solution

We know this formula

$\Delta \mathrm{G}=-\mathrm{n} F \mathrm{E}_{\text {cell }}$
$\Delta \mathrm{G}$ is negative, if $\mathrm{E}_{\text {cell }}$ is positive
$\quad$ Anode : $\mathrm{Cu}(\mathrm{s}) \longrightarrow \mathrm{Cu}^{+2}\left(\mathrm{C}_1\right)+2 \mathrm{e}^{-}: \mathrm{E}^{\circ}$
Cathode : $\mathrm{Cu}^{+2}\left(\mathrm{C}_2\right)+2 \mathrm{e}^{-} \longrightarrow \mathrm{Cu}(\mathrm{S}):-\mathrm{E}^{\circ}$
\hline \\
Cell reaction : $\mathrm{Cu}^{2+}\left(\mathrm{C}_2\right) \longrightarrow \mathrm{Cu}^{+2}\left(\mathrm{C}_1\right) \mathrm{E}_{\text {cell }}^{\circ}=0$
$\mathrm{E}_{\text {cell }}=\mathrm{E}_{\text {cell }}^{\circ}-\frac{2.303 \mathrm{RT}}{\mathrm{nF}} \log \mathrm{Q}$
$\mathrm{E}_{\text {cell }}=0-\frac{2.303 \mathrm{RT}}{\mathrm{nF}} \log \left(\frac{\mathrm{C}_1}{\mathrm{C}_2}\right)$
$\mathrm{E}_{\text {cell }}>0$; if $\frac{\mathrm{C}_1}{\mathrm{C}_2}<1 \Rightarrow \mathrm{C}_1<\mathrm{C}_2$

Only $C_2=\sqrt{2} C_1$ following the above condition.

Therefore, the correct option is (4).

Example.3

3. Calculate the emf (in V) of the following concentration cell at $25 ^\circ$

$\operatorname{Ag}(s)\left|\mathrm{AgNO}_3(0.01 \mathrm{M})\right|\left|\mathrm{AgNO}_3(0.05 \mathrm{M})\right| \mathrm{Ag}(\mathrm{s})$

1)-0.414

2)0.828

3)0.414

4) (correct)0.0414

Solution

The reaction occurring in the concentration cell can be represented as

$\begin{aligned} & \left(\mathrm{Ag}^{+}\right)_{\mathrm{c}} \\ & (0.05 \mathrm{M})\end{aligned}+(\mathrm{Ag})_{\mathrm{a}} \rightarrow(\mathrm{Ag})_{\mathrm{c}}+\quad \begin{array}{r}\left(\mathrm{Ag}^{+}\right)_a \\ (0.01 \mathrm{M})\end{array}$

$E=E^0-\frac{0.0591}{n} \log _{10} Q$

$\begin{aligned} & \mathrm{E}=0-\frac{0.0591}{1} \log _{10}\left(\frac{0.01}{0.05}\right) \\ & \mathrm{E}=0.0414 \mathrm{~V}\end{aligned}$

Hence, the answer is the option (4).

Example.4

4. A manganese electrode is immersed in a 2.0 M solution of MnCl₂ as cathode, and a manganese electrode is immersed in a 5.2 X 10^-2 solution of MnSO₄ as the anode (T= 25^o C). What is the emf (in V)?

1)0.47

2) (correct)0.047

3)0.083

4)0.83

Solution

This is a concentration cell

$\begin{aligned} & \mathrm{Mn}^{2+} \\ & 2 \mathrm{M}\end{aligned}+\underset{5.2 \times 10^{-2} \mathrm{M}}{\mathrm{Mn}^{2+}}$

$\begin{aligned} & \mathrm{E}_{\text {cell }}=\mathrm{E}^0-\frac{0.0591}{2} \log \left(\frac{5.2 \times 10^{-2}}{2}\right) \\ & \mathrm{E}_{\text {cell }}=0.047\end{aligned}$

Hence, the answer is the option (2).

Summary

Concentration cells are a crucial part of electrochemical studies, demonstrating how concentration differences can create an electrical potential, and they have various practical applications in chemistry and engineering. Concentration cells are used in various analytical techniques to measure ion concentrations in solutions. They help in understanding the effects of concentration gradients on electrochemical reactions and in studying electrode processes. Concentration cells are used in batteries and sensors where concentration differences drive the electrochemical reactions. The primary purpose of concentration cells is to explore and utilize the relationship between concentration differences and electrical potential, offering both theoretical and practical insights into electrochemical processes.