Depression in Freezing Point

The idea of depression at the freezing point was discovered by the French chemist Raoult in the late 19th century. He laid the main framework for the further discovery or advancement in the raoult's law. basically depression in the freezing point is the colligative property that is discovered in the deep study. Colligative properties are those that depend upon the number of solute particles and do not depend upon the nature of solute particles themselves. This phenomenon occurs because the presence of solute particles interferes with the formation of the solid phase of the solvent. Which lowers the temperature at which the solvent freezes.

This Story also Contains

1. Depression in freezing point
2. Some Solved Examples
3. Summary

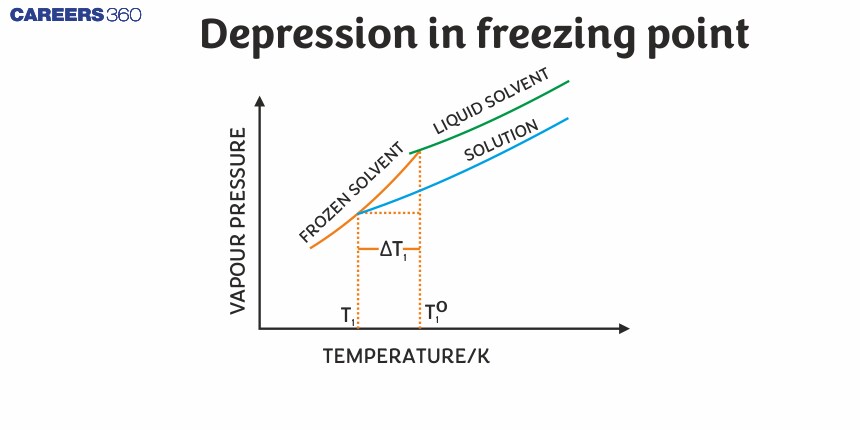
Depression in freezing point

Freezing Point: It is the temperature at which the liquid and the solid form of the same substance are in equilibrium and have the same vapour pressure. A solution freezes when its vapour pressure is equal to the vapor pressure of a pure solid solvent. Due to the lower vapor pressure of the solution, the solid form of a solution separates out at a lower temperature.

On adding a non-volatile solute to the solvent, the vapor pressure of the solution is lesser than the solvent and the vapor pressure of the solution becomes equal to the vapor pressure of the solid solvent at a lower temperature when compared to the pure solvent hence the freezing point of decreases.

Suppose $T_f^0$ and $T_f$ are the freezing points of pure solvent and solution respectively. The decrease in freezing point $\Delta T_f$ is given as:

$\Delta \mathrm{T}_{\mathrm{f}}=\mathrm{T}_{\mathrm{f}}^0-\mathrm{T}_{\mathrm{f}}$

• This is also termed as cryoscopy and depression of freezing point $\Delta T_f$
• For a dilute solution, $\Delta T_f$ is directly proportional to the molality (m) of the solution.

Hence $\Delta \mathrm{T}_{\mathrm{f}} \propto \mathrm{m}$
$\Delta T_f=K_f m$
If the molality of the solution is one, then
$\Delta T_f=K_f$
$\Delta T_f$ and M can be found out by using these relations.

$\begin{aligned} & \Delta T_f=K_f \times \frac{w}{M} \times \frac{1000}{W} \\ & M=\frac{K_f \times w \times 1000}{\Delta T_f \times W}\end{aligned}$

Here w = weight of solute
W = weight of solvent
K_f = molal depression constant or cryoscopic constant.
M = molar mass of solute

M1 = molar mass of solvent

The value of K_f or Cryoscopic constant is a property of the solvent only and does not depend on the type of solute. The value of K_f can be calculated as: $\mathrm{K}_{\mathrm{f}}=\frac{\mathrm{M}_1 \mathrm{RT}^2}{1000 \mathrm{~L}_{\mathrm{f}} \text { or } \Delta \mathrm{H}_{\text {fusion }}}$

Here, $\mathrm{L}_{\mathrm{f}}$ or $\Delta \mathrm{H}_{\mathrm{f}}=$ latent heat of fusion

Recommended topic video on ( Depression in Freezing Point)

Some Solved Examples

Example.1

1. The maximum freezing point falls in:

1) (correct)Camphor

2)Naphthalene

3)Benzene

4)Water

Solution

As we learned
Freezing -
Freezing occurs when liquid solvent is in equilibrium with solid solvent. As the non-volatile solute decreases, the vapour pressure freezing point decreases.
Camphor has the maximum value of $K_f(=39.7)$
Hence, the answer is the option (1).

Example.2

2. Calculate the molal depression constant of a solvent that has a freezing point 16.6⁰C and latent heat of fusion 180.75Jg^-1

1) (correct)3.86

2)2.68

3)4.68

4)2.886

Solution

As we learned

Dependence of K_f

$\begin{aligned} & K_f=\frac{R T_f^2 m}{1000 \Delta H_{\text {fusion }}} \\ & K_f=\frac{R T_f^2}{100 \times L_f}, R=8.314 \mathrm{JK}^{-1} \mathrm{~mol}^{-1} \\ & T_f=273+16.6=289.6 K ; L_f=180.75 \mathrm{Jg}^{-1} \\ & K_f=\frac{8.314 \times 289.6 \times 289.6}{1000 \times 180.75} \\ & K_f=3.86\end{aligned}$

Hence, the answer is the option (1).

Example.3

3. Elevation in the boiling point for 1 molal solution of glucose is 2K. The depression in the freezing point for 2 molal solutions of glucose in the same solvent is 2K. The relation between K_b and K_f is:

1)K_b = K_f

2)K_b =1.5 K_f

3)K_b =0.5 K_f

4) (correct)K_b =2 K_f

Solution

$\begin{aligned} & \frac{\Delta T_b}{\Delta T_f}=\frac{m \times K_b}{m \times K_f} \\ & \frac{2}{2}=\frac{1 \times K_b}{2 \times K_f} \\ & K_b=2 K_f\end{aligned}$

Hence, the answer is the option (4).

Example.4

4. The freezing point of a diluted milk sample is found to be $-0.2^0 \mathrm{C}$, while it should have been $-0.5^0 \mathrm{C}$ for pure milk. How much water has been added to pure milk to make the diluted sample?

1)2 cups of water to 3 cups of pure milk.

2) (correct)3 cups of water to 2 cups of pure milk.

3)1 cup of water to 3 cups of pure milk.

4)1 cup of water to 2 cups of pure milk.

Solution

The freezing point of milk $=-0.5^0 \mathrm{C} \because \Delta T_f=0.5^0 \mathrm{C}$

The freezing point of milk (diluted)$=-0.2^0 \mathrm{C} \because \Delta T_f=0.2^0 \mathrm{C}$

$\frac{\left(\Delta T_f\right) i}{\left(\Delta T_f\right) i i}=\frac{0.5}{0.2}=\frac{K_f m}{K_f m}=\frac{x(\text { mole }) \times \text { weight }(2)}{\text { weight }_{(1) \times} \times(\text { mole })}$

$W_2=\frac{5}{2} W_1$

Hence, the answer is the option (2).

Example.5

5. Molal depression constant for water is 1.86⁰C molal^-1. The freezing point (in ^oC ) of a 0.05 molal solution of a non-electrolyte in water is

1) (correct)-0.093

2)-0.33

3)-1.86

4)0.93

Solution

$\Delta T_f=K_f \times$ molality $=1.86 \times 0.05=0.093^{\circ} \mathrm{C}$

Thus freezing point $=0-0.093=-0.093 C^0$

Hence, the answer is (-0.093).

Summary

The concept of depression in freezing point is observed when by adding solute in the solvent the freezing point of the solution decreases and basically it is a colligative property these arr those property Which depend upon the number of the solutes, not on the nature of the solute. This colligative property has various benefits as It is used in the automobile industry aur the automotive industry it is used to make an anti-freezing solution by lowering the freezing point of the coolant and these solutions are used to prevent the formation of ice in the engine or in fuel in very low temperatures to ensure the efficiency of the engine and prevent them from any damage.