Elevation in Boiling Point

The elevation in boiling point is the colligative property of the Solutions. Which depends upon the number of the solute particles as it depends on the number, not on the nature of the solute. When the phenomenon of elevation in boiling point developed it was not understood Scientists of ancient times observed that adding substances to water could change their boiling point. In 1814 a French chemist studied this phenomenon and his name is Francois Marie Roult he formulated Raoult's Law and described how the vapour pressure of solvent decreases when the volatile solute is added which the framework of elevation in boiling point after that another scientist Jacobus Henricus van't Hoff extends the Raoult's law and introduce the concept of colligative properties i.e elevation in boiling point

This Story also Contains

1. Elevation in boiling point
2. Some Solved Examples
3. Summary

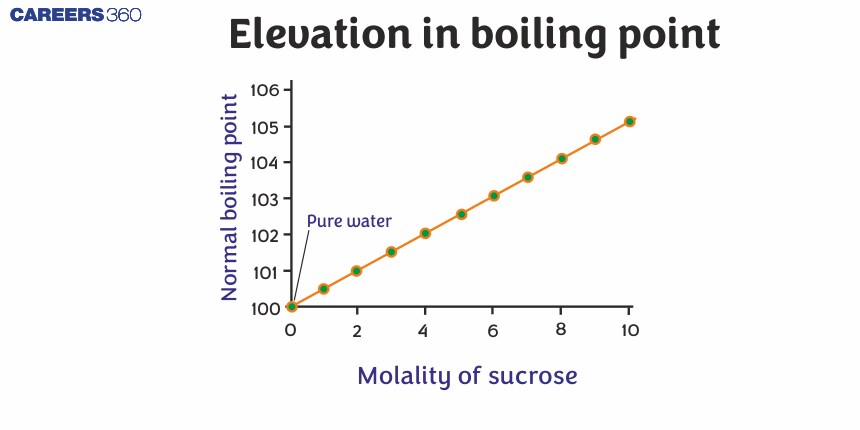
Elevation in boiling point

Boiling Point: It is the temperature of a liquid at which its vapour pressure becomes equal to the atmospheric pressure.

Now, the lowering of the vapour pressure of the solution occurs when the addition of non-volatile solute in solvent happens. In order to boil the solution, it is necessary to increase the temperature of the solution above the boiling point of the pure solvent. It means the boiling point of the solution is always higher than the boiling point of the pure solvent. This increase in the boiling point of the solution is called elevation in boiling point$\left ( \Delta T_b \right )$

• It is also termed as Ebullioscopy.

• Suppose $\mathrm{T}_{\mathrm{b}}^{\mathrm{o}}$ and $\mathrm{T}_{\mathrm{b}}$ are the B.P. of pure solvent and solution respectively, then elevation in B.P $\left(\Delta \mathrm{T}_{\mathrm{b}}\right)$ is given as $\Delta \mathrm{T}_{\mathrm{b}}=\mathrm{T}_{\mathrm{b}}-\mathrm{T}_{\mathrm{b}}^{\circ}$

$\Delta \mathrm{T}_{\mathrm{b}}$ is directly proportional to the molality of the solution

$\begin{aligned} & \Delta \mathrm{T}_{\mathrm{b}} \propto \mathrm{m} \\ & \Delta \mathrm{T}_{\mathrm{b}}=\mathrm{K}_{\mathrm{b} \mathrm{m}}\end{aligned}$

• If the molality of the solution is one, then

$\Delta \mathrm{T}_{\mathrm{b}}=\mathrm{K}_{\mathrm{b}}$

• The elevation in B.P. is also given as$\Delta \mathrm{T}_{\mathrm{b}}=\mathrm{K}_{\mathrm{b}} \times \frac{\mathrm{w}}{\mathrm{M}} \times \frac{1000}{\mathrm{~W}}$

• The molecular weight of solute can be found out as follows$\mathrm{M}=\frac{\mathrm{K}_{\mathrm{b}} \times \mathrm{w} \times 1000}{\Delta \mathrm{T}_{\mathrm{b}} \times \mathrm{W}}$

Here w = weight of solute

W = weight of solvent
Kb= molal elevation constant or ebullioscopic constant.
M = molar mass of solute

M₁ = molar mass of solvent

The value of $K_b$ or Ebullioscopic constant is a property of the solvent only and does not depend on the type of solute. The value of $K_b$ can be calculated as:

$\mathrm{K}_{\mathrm{b}}=\frac{\mathrm{RM}_1 \mathrm{~T}^2}{1000 \mathrm{Lv} \text { or } \Delta \mathrm{Hv}}$

Here L_v or $\Delta \mathrm{T}_{\mathrm{b}}=\mathrm{K}_{\mathrm{b}} \times \frac{\mathrm{w}}{\mathrm{M}} \times \frac{1000}{\mathrm{~W}}$= latent heat of vaporization.

Recommended topic video on ( Elevation in Boiling Point)

Some Solved Examples

Example.1

1. When a substance is dissolved in a solvent, the vapour pressure of the solvent decreases. It brings:

1)A decrease in the boiling point of the solution

2) (correct)An increase in the boiling point of the solution

3)A decrease in the freezing point of the solution

4)An increase in the freezing point of the solution

Solution

Elevation in Boiling point -
The boiling point increases because vapour pressure decreases.

Boiling point $\propto \frac{1}{\text { vapour pressure of liquid }}$

Hence, on decreasing vapour pressure, the boiling point will increase.

Therefore, option(2) is correct

Example.2

2. Which of the following statements is correct for the boiling point of the solvent containing a dissolved solid substance:

1) The boiling point of the liquid is depressed

2) (correct)Boiling point of the liquid is elevated

3)There is no effect on the boiling point

4)The change depends upon the polarity of the liquid

Solution

Elevation in Boiling point -
The boiling point increases because vapour pressure decreases.

Dissolution of a non-volatile solute raises the boiling pt. of a liquid.

Therefore, option(2) is correct

Example.3

3. Pressure cooker reduces cooking time for food because:

1)Heat is more evenly distributed in the cooking space.

2) (correct) The Boiling point of water involved in cooking is increased.

3)The higher pressure inside the cooker crushes the food material.

4)Cooking involves chemical changes helped by a rise in temperature.

Solution

Elevation in Boiling point -
The boiling point increases because vapour pressure decreases.

Due to higher pressure inside the cooker, the boiling point elevated.

Therefore, option(2) is correct

Example.4

4. Elevation in the boiling point for 1 molal solution of glucose is 2K. The depression in the freezing point for 2 molal solution of glucose in the same solvent is 2K. The relation between K_b and K_f is:

1)K_b = K_f

2)K_b =1.5 K_f

3)K_b =0.5 K_f

4) (correct)K_b =2 K_f

Solution

$\begin{aligned} & \frac{\Delta T_b}{\Delta T_f}=\frac{m \times K_b}{m \times K_f} \\ & \frac{2}{2}=\frac{1 \times K_b}{2 \times K_f} \\ & K_b=2 K_f\end{aligned}$

Hence, the answer is the option (4).

Example.5

5. If 0.15g of a solute dissolved in 15g of solvent is boiled at a temperature higher by 0.216⁰C than that of the pure solvent. The molecular weight of the substance (molal elevation constant for the solvent is 2.16⁰C ) is

1) (correct)100

2)10

3)20.2

4)0.1

Solution

$\begin{aligned} & \Delta T_b=K_b m \\ & K_b=\text { Boiling point elevation constant } \\ & m=\text { molality } \\ & m=\frac{K_b \times w \times 1000}{\Delta T_b \times W}=\frac{2.16 \times 0.15 \times 1000}{0.216 \times 15}=100\end{aligned}$

Hence, the answer is (100g/mol).

Example.6

6.The rise in the boiling point of a solution containing 1.8 gram of glucose in 100 g of a solvent in 0.1⁰C. The molal elevation constant of the liquid is:

1)$0.01 \mathrm{~K} / \mathrm{m}$

2)$0.1 \mathrm{~K} / \mathrm{m}$

3) (correct)$1 \mathrm{~K} / \mathrm{m}$

4)$10 \mathrm{~K} / \mathrm{m}$

Solution

$\begin{aligned} \Delta T_b & =K_b m \\ K_b & =\frac{\Delta T_b}{m}=\frac{0.1 \times 100}{\frac{1.8}{180} \times 1000}=1 \mathrm{~K} / \mathrm{m}\end{aligned}$

Hence, the answer is the option (3).

Summary

It is found that the boiling point of the solution is always higher than that of the pure Solvent. The increase is called elevation in boiling point. The reason for the elevation in boiling point may be that we know that the vapour pressure of the solution is lower than that of the pure solvent and vapour pressure increases with the increase in temperature. Hence, the solution has to be heated more to make the vapour pressure equal to the atmospheric pressure. And this elevation in boiling point is measured by the ebullioscopic method. This colligative property has various applications including in cooking as adding salt to the water to increase its boiling point by which the food is cooked faster and also has several other benefits in the case of the chemical industry as preparing the solution it help in designing the process where boiling point is required to avoid the overheat to control the rates of reaction.