Energy Level Diagram

Energy level diagrams are graphical representations showing the relative energies of atomic or molecular orbitals. An energy level diagram would portray energy levels normally in the form of horizontal lines, such that the higher the position of the energy level, the more it is in energy. It is interpreted that these levels are occupied by electrons governed by the rules of quantum mechanics, in particular, the Aufbau principle, Pauli's exclusion principle, and Hund's rule.

JEE Main 2025: Chemistry Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics |  PYQs

This Story also Contains

1. Molecular Orbital Energy Diagrams
2. Some Solved Examples
3. Summary

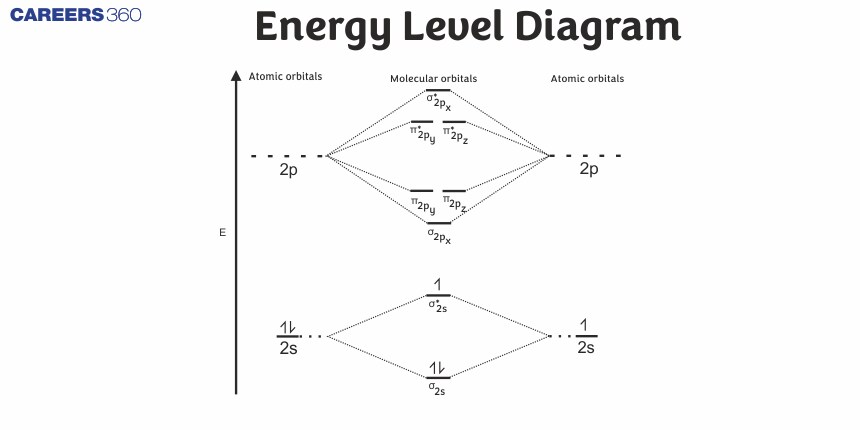
Molecular Orbital Energy Diagrams

The relative energy levels of atomic and molecular orbitals are typically shown in a molecular orbital diagram. As given in the figure below, for a diatomic molecule, the atomic orbitals of one atom are shown on the left, and those of the other atom are shown on the right. Each horizontal line represents one orbital that can hold two electrons. The molecular orbitals formed by the combination of the atomic orbitals are shown in the center. Dashed lines show which of the atomic orbitals combine to form the molecular orbitals. For each pair of atomic orbitals that combine, one lower-energy (bonding) molecular orbital and one higher-energy (antibonding) orbital result. Thus we can see that combining the six 2p atomic orbitals results in three bonding orbitals (one σ and two π) and three antibonding orbitals (one σ* and two π*).

molecular orbital diagram

The molecular orbitals are filled in the same manner as atomic orbitals, using the Aufbau principle and Hund’s rule.

Bond Order

The filled molecular orbital diagram shows the number of electrons in both bonding and antibonding molecular orbitals. The net contribution of the electrons to the bond strength of a molecule is identified by determining the bond order that results from the filling of the molecular orbitals by electrons.

The bond order is calculated by subtracting the destabilizing (antibonding) electrons from the stabilizing (bonding) electrons. Since a bond consists of two electrons, we divide by two to get the bond order. We can determine bond order with the following equation:

bond order = [(number of bonding electrons)−(number of antibonding electrons)]/2

The order of a covalent bond is a guide to its strength; a bond between two given atoms becomes stronger as the bond order increases. If the distribution of electrons in the molecular orbitals between two atoms is such that the resulting bond would have a bond order of zero, a stable bond does not form.

For example, the bond order of H₂ molecule is given as follows:

The molecular orbital energy diagram predicts that H₂ will be a stable molecule with lower energy than the separated atoms.

A dihydrogen molecule contains two bonding electrons and no antibonding electrons so we have:

bond order in H₂=(2−0)/2=1

Because the bond order for the H–H bond is equal to 1, the bond is a single bond.

Magnetic Moment

The magnetic behavior of any molecule can be determined from the number of unpaired electrons in the bonding and antibonding orbitals. The molecule is said to be diamagnetic as there is no unpaired electron present in the orbitals and not attracted by the magnet. But if any unpaired electron is present then the molecule is paramagnetic.

For example, O₂ molecule has 2 unpaired electrons can be seen from the diagram below:

Therefore, O₂ molecule is paramagnetic.

Recommended topic video on (Energy level diagram)

Some Solved Examples

Example 1: When two atoms of chlorine combine to form one molecule of chlorine gas, the energy of the molecule?

1)Greater than that of the separate atom

2)Equal to that of the separate atom

3) Lower than that of separate atoms

4)None of the above

Solution

Energy level diagram for molecular orbitals. -

1s atomic orbitals combine to give $\sigma(1 s)_{\text {and }} \sigma^*(1 s)$. 2s and 2p atomic orbitals give rise to eight molecular orbitals.

When bonds form between two atoms then their energy gets lower than that of the separate atom as the bond formation is exothermic.

Example 2: Among the following species, the diamagnetic molecule is :

1) NO
2) CO
3) $B_2$
4) $O_2$

Solution

If the molecular orbitals have unpaired electrons then the molecule will be paramagnetic.

or if all are paired then the molecule will be diamagnetic.

In CO, molecular orbital configuration

$\sigma_{1 s}^2, \sigma_{1 s}^{* 2}, \sigma_{2 s}^2, \sigma_{2 s}^{* 2}, \pi_{2 p_x}^2=\pi_{2 p_y}^2, \sigma_{2 p_z}^2$

There are no unpaired electrons thus CO is a diamagnetic.

Hence, the answer is the option (2).

Example 3: Among the following molecules/ions, $C_2^{2-}, N_2^{2-}, O_2^{2-}, O_2$ which one is diamagnetic and has the shortest bond length?

1) $\mathrm{O}_2$
2) $\mathrm{N}_2^{2-}$
3) $\mathrm{O}_2^{2-}$
4) $C_2^{2-}$

Solution

$C_2^{2-}:-$ No of electrons $=14$
$
\sigma_{1 S}^2 \sigma_{1 S^2}^* \sigma_{2 S}^2 \sigma_{2 S^2}^* \pi_{2 p x}^2=\pi_{2 p y}^2 \sigma_{2 p z^2}
$
(1) It is diamagnetic
(2) Bond order $=\frac{10-4}{2}=3$
$
\begin{aligned}
& O_2^{2-}: \text { - No of electrons=18 } \\
& \sigma_{1 S}^2 \sigma_{1 S^2}^* \sigma_{2 S}^2 \sigma_{2 S^2}^* \sigma 2 p z^2 \pi 2 p x^2=\pi_{2 p y}^2 \pi_{2 p x^2}^*=\pi_{2 p y^2}^*
\end{aligned}
$
(1) It is diamagnetic
(2) Bond Order $=\frac{10-8}{2}=1$
$\because$ B.O $\propto \frac{1}{\text { Bond length }}$
$\therefore$ The correct answer is $\mathrm{C}_2^{2-}$

Hence, the answer is the option (4).

Example 4: From elementary molecular orbital theory we can give the electronic configuration of the singly positive nitrogen molecule ion N₂⁺ as:

$\begin{aligned} & \text { 1) } \sigma(1 S)^2 \sigma^*(1 S)^2 \sigma(2 S)^2 \sigma^*(2 S)^2 \pi(2 P)^4 \sigma(2 P)^1 \\ & \text { 2) } \sigma(1 S)^2 \sigma^*(1 S)^2 \sigma(2 S)^2 \sigma^*(2 S)^2 \sigma(2 P)^1 \pi(2 P)^3 \\ & \text { 3) } \sigma(1 S)^2 \sigma^*(1 S)^2 \sigma(2 S)^2 \sigma^*(2 P)^2 \pi(2 P)^4 \\ & \text { 4) } \sigma(1 S)^2 \sigma^*(1 S)^2 \sigma(2 S)^2 \sigma^*(2 S)^2 \sigma(2 P)^2 \pi(2 P)^2\end{aligned}$

Solution

Energy order for B₂, C₂, N₂, Li₂, Be₂ -

$\begin{aligned} & \sigma(1 s)<\sigma^*(1 s)<\sigma(2 s)<\sigma^*(2 s)<\pi\left(2 p_x\right)=\pi\left(2 p_y\right)<\sigma\left(2 p_z\right)<\pi^*\left(2 p_X\right)= \\ & \pi^*\left(2 p_y\right)<\pi^*\left(2 p_z\right)\end{aligned}$

$\sigma(1 S)^2 \sigma^*(1 S)^2 \sigma(2 S)^2 \sigma^*(2 S)^2 \pi(2 P)^4 \sigma(2 P)^1$

Example 5: In an oxygen molecule, $\sigma 2 p$ molecular orbital has lower energy than $\pi 2 p$ orbitals. This is due to:

1)Mixing of sp orbitals of the two oxygen atoms

2) Non-mixing of an sp orbital of the two oxygen atoms.

3)The inclusion of d- d-orbitals in the molecular orbitals

4)Electronic repulsion between the electrons of the two atoms.

Solution

The energy level diagram for oxygen molecules is:

For most of the elements, $\sigma(2 p)$ orbital lies at higher energy than $\pi(2 p)$ orbitals because the difference between $2 s$ and $2 p$ atomic energy levels is small (except in case of $O_2$ and $F_2$ where the difference in energy levels of $2 s$ and $2 p$ is large). As a result, $\sigma(2 s)$ and $\sigma(2 p)$ are so close together that the repulsive forces between the electrons present in them raise the energy of $\sigma(2 p)$ above that of $\pi(2 p)$ molecular orbitals. Therefore, In oxygen molecule, $\sigma(2 p)$ molecular orbital has lower energy than $\pi(2 p)$ orbitals because of Non- mixing of an sp orbital of the two oxygen atoms.

Hence, option number (2) is correct.

Summary

For atomic systems, these diagrams portray electron configurations within shells and subshells. The molecular orbital diagrams approximate the way atomic orbitals combine to form bonding and antibonding orbitals in molecular systems. This enables one to understand and predict molecular stability, bond order, and magnetic properties.