Entropy Change

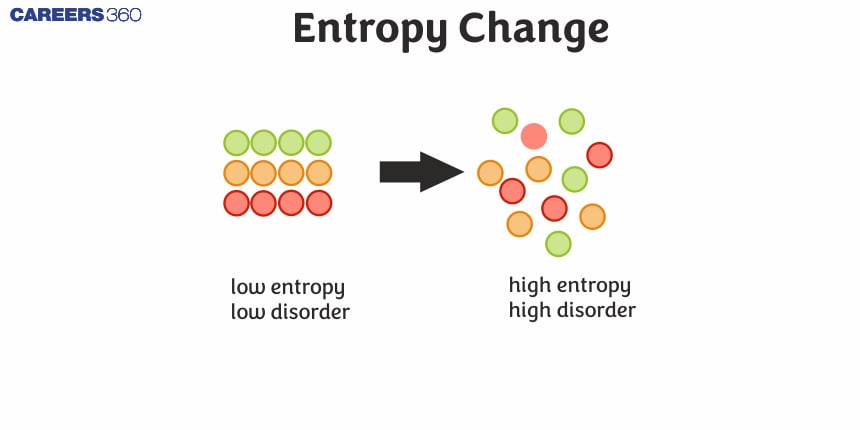
Entropy is one of the most basic principles not only in thermodynamics but also in statistical mechanics. It is often considered a measure of the disorder or randomness of a system. The change of entropy depends only upon the states of the system at the start and end, and not on the path taken. The Second Law of Thermodynamics says that the entropy of any isolated system cannot diminish; hence, it will always remain at an increased value or constant, thereby making entropy in the universe ever-increasing. Entropy change is represented by ΔS, which is actually a measure for a process determined by the heat transfer, Q, in relation to the temperature at which it is transferred, T: ΔS = Q / T. This relationship holds good for reversible processes. For irreversible processes, the entropy change is always greater.

This Story also Contains

1. Mathematical Definition of Entropy
2. Entropy Changes in Different Processes
3. Some Solved Examples
4. Summary

Mathematical Definition of Entropy

Clausius defined a reversible isothermal process as the integral of all the terms involving heat exchange (q) divided by the absolute temperature T.

$\mathrm{dS}=\frac{\mathrm{dq}_{\mathrm{rev}}}{\mathrm{T}}$ or $\Delta \mathrm{S}=\frac{\mathrm{q}_{\mathrm{rev}}}{\mathrm{T}}$

Unit of entropy is $\frac{\mathrm{J}}{\mathrm{mol}-\mathrm{K}}$

Here mol^-1 is also used as entropy being an extensive property that depends upon the amount of the substance.

Entropy Changes in Different Processes

1. Isothermal reversible process

For a reversible isothermal process, $\Delta \mathrm{E}=0$

So $\mathrm{q}=-\mathrm{w}$

$\therefore \Delta \mathrm{S}=\frac{-\mathrm{w}}{\mathrm{T}}=\frac{2.303 \mathrm{nRT} \log \left(\frac{\mathrm{V}_2}{\mathrm{~V}_1}\right)}{\mathrm{T}}$

$\therefore \Delta \mathrm{S}=2.303 \mathrm{nR} \log \left(\frac{\mathrm{V}_2}{\mathrm{~V}_1}\right)=2.303 \mathrm{nR} \log \left(\frac{\mathrm{P}_1}{\mathrm{P}_2}\right)$

2. Adiabatic reversible process

As $q=0$, so $\Delta S=0$

Note: Reversible adiabatic process is also called an Isentropic process

3. Isobaric process:

$\Delta \mathrm{S}=2.303 \mathrm{nC}_{\mathrm{P}} \log \left(\frac{\mathrm{T}_2}{\mathrm{~T}_1}\right)=2.303 \mathrm{nC}_{\mathrm{P}} \log \left(\frac{\mathrm{V}_2}{\mathrm{~V}_1}\right)$

4. Isochoric process:

$\Delta \mathrm{S}=2.303 \mathrm{nC}_{\mathrm{V}} \log \left(\frac{\mathrm{T}_2}{\mathrm{~T}_1}\right)=2.303 \mathrm{nC}_{\mathrm{V}} \log \left(\frac{\mathrm{P}_2}{\mathrm{P}_1}\right)$

5. Entropy change in a process where both the Temperature, as well as Volume or Pressure, is changing

$\Delta \mathrm{S}=\int \frac{\mathrm{dq}}{\mathrm{T}}=\int \frac{(\mathrm{dE}-\mathrm{dw})}{\mathrm{T}}$

$\Delta S=\int \frac{\mathrm{nC}_{\mathrm{v}} \mathrm{dT}+\mathrm{PdV}}{\mathrm{T}}=\int_{\mathrm{T}_1}^{\mathrm{T}_2} \frac{\left(\mathrm{nC}_{\mathrm{v}} \mathrm{dT}\right)}{\mathrm{T}}+\int_{\mathrm{V}_1}^{\mathrm{V}_2} \frac{(\mathrm{nRdV})}{\mathrm{V}}$

$\Delta \mathrm{S}=\mathrm{nC}_{\mathrm{v}} \ln \left(\frac{\mathrm{T}_2}{\mathrm{~T}_1}\right)+\mathrm{nR} \ln \left(\frac{\mathrm{V}_2}{\mathrm{~V}_1}\right)$

The above equation can also be written in terms of Pressure as

$\Delta \mathrm{S}=\mathrm{nC}_{\mathrm{p}} \ln \left(\frac{\mathrm{T}_2}{\mathrm{~T}_1}\right)+\mathrm{nR} \ln \left(\frac{\mathrm{P}_1}{\mathrm{P}_2}\right)$

Note: Remember the above general formula for the change in entropy.

6. Entropy change in irreversible processes:

Suppose a system at higher temperature T₁ and its surroundings is at lower temperature T₂. 'q' amount of heat goes irreversibly from the system to the surroundings.

$\Delta \mathrm{S}_{\text {system }}=-\frac{\mathrm{q}}{\mathrm{T}_1}$

$\Delta \mathrm{S}_{\text {surroundings }}=+\frac{\mathrm{q}}{\mathrm{T}_2}$

$\Delta S_{\text {process }}=\Delta S_{\text {system }}+\Delta S_{\text {surroundings }}=-\frac{q}{T_1}+\frac{q}{T_2}=q \frac{\left[T_1-T_2\right]}{T_1 T_2}$

$\begin{aligned} & \because \mathrm{T}_1>\mathrm{T}_2 \\ & \therefore \mathrm{T}_1-\mathrm{T}_2>0\end{aligned}$

$\therefore \Delta \mathrm{S}_{\text {process }}>0$

So entropy increases in an irreversible process like conduction, radiation, etc.

7. Entropy changes during phase transition:

$\Delta \mathrm{S}=\mathrm{S}_2-\mathrm{S}_1=\frac{\mathrm{q}_{\mathrm{rev}}}{\mathrm{T}}=\frac{\Delta \mathrm{H}}{\mathrm{T}}$

8. Entropy change when liquid is heated:

When a definite amount of liquid of mass 'm' and specific heat 's' is heated

Let us suppose a small amount of heat dq is added and as a result, the temperature of the body increases by dT temperature

$\mathrm{dq}=\mathrm{m} \times \mathrm{s} \times \mathrm{dT}$

$\therefore \mathrm{dS}=\frac{\mathrm{dq}}{\mathrm{T}}=\frac{\mathrm{m} \times \mathrm{s} \times \mathrm{dT}}{\mathrm{T}}$

$\therefore \Delta \mathrm{S}=\mathrm{m} \times \mathrm{s} \times \log \frac{\mathrm{T}_2}{\mathrm{~T}_1}$

9. Entropy Change in Mixing of Ideal Gases:

Suppose n₁ mole of gas 'P' and n₂ mole of gas Q' are mixed; then total entropy change can be calculated as:

$\Delta \mathrm{S}=-2.303 \mathrm{R}\left[\mathrm{n}_1 \log _{10} \mathrm{X}_1+\mathrm{n}_2 \log _{10} \mathrm{X}_2\right]$

Here X₁ and X₂ are mole fractions of gases P and Q respectively.

$\Delta \mathrm{S} / \mathrm{mol}=-2.303 \mathrm{R} \frac{\left[\mathrm{n}_1 \log _{10} \mathrm{X}_1\right.}{\mathrm{n}_1+\mathrm{n}_2}+\frac{\left.\mathrm{n}_2 \log _{10} \mathrm{X}_2\right]}{\mathrm{n}_1+\mathrm{n}_2}$

$\Delta \mathrm{S} / \mathrm{mol}=-2.303 \mathrm{R}\left[\mathrm{X}_1 \log _{10} \mathrm{X}_1+\mathrm{X}_2 \log _{10} \mathrm{X}_2\right]$

It can be seen that the above expression is always positive for $\Delta \mathrm{S}$.

For a reversible isothermal process, Clausius defined it as the integral of all the terms involving heat exchange (q) divided by the absolute temperature T.

$\mathrm{dS}=\frac{\mathrm{dq}_{\mathrm{rev}}}{\mathrm{T}}$ or $\Delta \mathrm{S}=\frac{\mathrm{q}_{\mathrm{rev}}}{\mathrm{T}}$

Unit of entropy is $\frac{\mathrm{J}}{\mathrm{mol}-\mathrm{K}}$

Here mol^-1 is also used as entropy being an extensive property that depends upon the amount of the substance.

Recommended topic video on (Entropy Change)

Some Solved Examples

Example 1: When one mole of an ideal gas is compressed to half of its initial volume and simultaneously heated to twice its initial temperature, the change in entropy of gas ($\Delta S$) is :

1)$\mathrm{C}_{\mathrm{p}, \mathrm{m}} \ln 2$

2)$\mathrm{C}_{\mathrm{v}, \mathrm{m}} \ln 2$

3)$\mathrm{R} \ln 2$

4) $\left(\mathrm{C}_{\mathrm{v}, \mathrm{m}}-\mathrm{R}\right) \ln 2$

Solution

As we learned,

Change in entropy for ideal gas in terms of C_v -

$\Delta \mathrm{S}_{\text {system }}=\mathrm{nC}_{\mathrm{v}} \ln \frac{\mathrm{T}_2}{\mathrm{~T}_1}+\mathrm{nR} \ln \frac{\mathrm{V}_2}{\mathrm{~V}_1}$

$\Delta \mathrm{S}=\mathrm{C}_{\mathrm{v}, \mathrm{m}} \ln 2+\mathrm{R} \ln \left[\frac{1}{2}\right]=\left(\mathrm{C}_{\mathrm{v}, \mathrm{m}}-\mathrm{R}\right) \ln 2$

Example 2: For which of the following processes, ΔS is negative?

1)$\mathrm{H}_2(\mathrm{~g}) \rightarrow 2 \mathrm{H}(\mathrm{g})$

2) $N_2(g, 1 \mathrm{~atm}) \rightarrow N_2(\mathrm{~g}, 5 \mathrm{~atm})$

3)$C($ diamond $) \rightarrow C($ graphite $)$

4)$N_2(g, 273 K) \rightarrow N_2(g, 300 K)$

Solution

The change in entropy for an ideal gas in terms of C(p) -

$\Delta S_{\text {system }}=n C_P \ln \frac{T_f}{T_i}+n R \ln \frac{P_i}{P_f}$

Where,

$C_p=$ Molar heat capacity at constant pressure

Now,

$N_2(\mathrm{~g})(1 \mathrm{~atm}) \rightarrow N_2(\mathrm{~g})(5 \mathrm{~atm})$

$\Delta S=\left(n C_p \ln \frac{T_2}{T_1}\right)+n R \ln \frac{V_2}{V_1}$

for isothermal process

$T_1=T_2$ and $\quad V_2 / V_1=P^1 / P^2$

$\Delta S=0+n R \ln \frac{P_1}{P_2}$

$\Delta S=0+n R \ln \frac{1}{5}$

$\Delta S<0$

Example 3: The molar heat capacity (C_p) of CD₂O is 10 cals at 1000 K. The change in entropy (in cal deg^-1) associated with cooling of 32 g of CD₂O vapor from 1000 K to 100 K at constant pressure will be :

(D = deuterium, at. mass = 2 u)

1)23.03

2) -23.03

3)2.303

4)-2.303

Solution

Entropy for isobaric process -

$\Delta \mathrm{S}=\mathrm{nC}_{\mathrm{p}} \ln \frac{\mathrm{T}_{\mathrm{f}}}{\mathrm{T}_{\mathrm{i}}}$

$\begin{aligned} & \Delta \mathrm{S}=\mathrm{nC}_{\mathrm{p}} 1 \mathrm{n}\left(\frac{\mathrm{T}_2}{\mathrm{~T}_1}\right) \\ & \Delta \mathrm{S}=2.303 \times \mathrm{n} \times \mathrm{C}_{\mathrm{p}} \log \left(\frac{\mathrm{T}_2}{\mathrm{~T}_1}\right)\end{aligned}$

$\Delta \mathrm{S}=2.303 \times 1 \times 10 \log \left(\frac{100}{1000}\right)$

$\Delta \mathrm{S}=-23.03 \mathrm{cal} \mathrm{deg}^{-1}$

Hence, the answer is the option (2).

Example 4: In conversion of limestone to lime,$\mathrm{CaCO}_{3(s)} \rightarrow \mathrm{CaO}_{(s)}+\mathrm{CO}_{2(g)}$ the values of $\Delta H^{\circ}$ and $\Delta S^{\circ}$ are +179.1 kJ mol-1 and 160.2 J/K respectively at 298 K and 1 bar. Assuming that $\Delta H^{\circ}$ and $\Delta S^{\circ}$ do not change with temperature, temperature (in K) above which conversion of limestone to lime will be spontaneous is

1) 1118

2)1008

3)1200

4)845

Solution

Entropy for phase transition at constant pressure -

$\Delta S=\frac{\Delta H_{\text {Transition }}}{T}$

Where,

Transition $\Rightarrow$ Fusion, Vaporisation, Sublimation

$\Delta H \Rightarrow$Enthalpy

$\Delta E \Rightarrow$Internal Energy

$T \Rightarrow$Transitional temperature

$\begin{aligned} & \Delta S=\frac{\Delta H}{T} \\ & T=\frac{\Delta S}{\Delta H}=\frac{179.1 \times 10^3}{160.2} \\ & H=1117.97 K=1118 K\end{aligned}$

Hence, the answer is the option (1).

Summary

Entropy change (∆S) is used as the measure of disorder or randomness of the system in a process, and it is basic to the Second Law of Thermodynamics. The second law, in particular, states that the entropy of an isolated system can never decrease, so the natural trend is always toward increasing disorder. It is defined as the change in entropy that is calculated by dividing heat transferred by the temperature: ΔS = Q/T. The change in entropy can thus be used to evaluate spontaneity; a plus total entropy change means a process is spontaneous. Entropy change can also, in chemical reactions, be predicted by the states of reactants and products. Gases have more entropy than liquids or solids. The entropy change is also one of the components in the definition of Gibbs free energy, ΔG, defining the spontaneity or non-spontaneity of a reaction at constant pressure and temperature. Entropy change, therefore, becomes central in predicting the natural direction of processes and in designing effective energy systems.