Hess’s Law

Hess's Law is a basic rule in thermodynamics and chemistry, named for Germain Hess. It simply states that the net enthalpy change for a chemical reaction is independent of the pathway taken. It is developed directly from the first law of thermodynamics, a conservation of energy law. In this respect, Hess's Law becomes very useful, since it allows one to calculate enthalpy changes for reactions where direct measurement is difficult. That is, if the enthalpy changes of individual steps or simpler reactions involved in a complex reaction are known, then its overall enthalpy change will be easily determined.

JEE Main 2025: Chemistry Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics |  PYQs

This Story also Contains

1. Hess's Law
2. Applications of Hess Law:-
3. Some Solved Examples
4. Summary

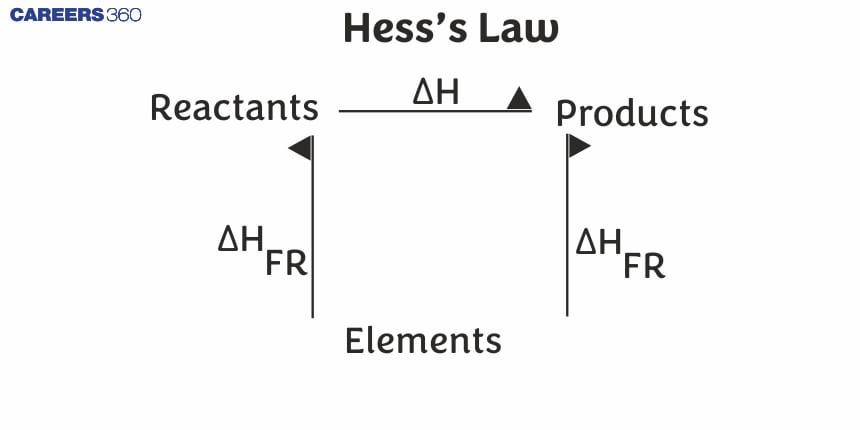
Hess's Law

This rule is a consequence of the Enthalpy or Internal energy being a state function.

According to Hess's Law, "The enthalpy change for a process is independent of path or way of a process. The enthalpy change ($\Delta$H or $\Delta$E for any physical or chemical process remains the same whether the process is carried out in one step or in many steps. "

Let us consider the following example

$\begin{aligned} & \mathrm{C}+\mathrm{O}_2 \rightarrow \mathrm{CO}_2 ; \Delta \mathrm{H}_1=-94.3 \mathrm{kcal} \\ & \mathrm{C}+\frac{1}{2} \mathrm{O}_2 \rightarrow \mathrm{CO} ; \Delta \mathrm{H}_2=-68.3 \mathrm{kcal} \\ & \mathrm{CO}+\frac{1}{2} \mathrm{O}_2 \rightarrow \mathrm{CO}_2 ; \Delta \mathrm{H}_3=-26 \mathrm{kcal}\end{aligned}$

It can be seen that $\Delta \mathrm{H}_1=\Delta \mathrm{H}_2+\Delta \mathrm{H}_3$

Hence it proves that

• $\Delta$H or $\Delta$E is not proportional to the path or way of reaction
• $\Delta$H or $\Delta$E is a state function that depends only on the initial and final state (state function).

Applications of Hess Law:-

It has the following applications:

1. It helps in finding enthalpy changes for those reactions also which are experimentally not possible.

2. It also helps in finding $\Delta \mathrm{H}_{\text {formation }}, \Delta \mathrm{H}_{\text {combustion }}$ etc.

3. For the determination of resonance energy and lattice energy.

4. For the determination of enthalpies of reactions occurring very slowly.

Recommended topic video on (Hess’s Law)

Some Solved Examples

Example 1: The enthalpy change for a reaction does not depend upon the

1)physical states of reactants and products

2)use of different reactants for the same product

3) nature of intermediate reaction steps

4)difference in initial or final temperatures of involved substances.

Solution

As we learned from the concept:

Hess's law of constant heat summation states that regardless of the multiple stages or intermediate steps of the reaction the total enthalpy change for the reaction is the sum of all changes.

The enthalpy of a chemical process is independent of the path taken from the initial and the final state.

Example 2: The enthalpy of combustion of propane, graphite and dihydrogen at 298 K are $-2220.0 \mathrm{~kJ} \mathrm{~mol}^{-1},-393.5 \mathrm{~kJ} \mathrm{~mol}^{-1}$ and $-285.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$ respectively. The magnitude of enthalpy of formation of propane $\left(\mathrm{C}_3 \mathrm{H}_8\right)$ is ___________$\mathrm{kJ} \mathrm{mol}^{-1}$ (Nearest integer)

1) 103.7

2)120.25

3)456.22

4)653

Solution

Given the combustion enthalpy -

(1) $\mathrm{C}_3 \mathrm{H}_8(\mathrm{~g})+5 \mathrm{O}_2 \longrightarrow 3 \mathrm{CO}_2+4 \mathrm{H}_2 \mathrm{O}, \Delta \mathrm{H}_1=-2220.0 \mathrm{~kJ} / \mathrm{mol}$

(2) $\mathrm{C}_{(\mathrm{s})}+\mathrm{O}_2 \longrightarrow \mathrm{CO}_2 \quad \Delta_{\mathrm{c}} \mathrm{H}_2=-393.5 \mathrm{~kJ} / \mathrm{mol}$

(3) $\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2 \rightarrow \mathrm{H}_2 \mathrm{O} \quad \Delta_{\mathrm{c}} \mathrm{H}_3=-285.8 \mathrm{~kJ} / \mathrm{mol}$

After doing $3 \times(2)+4 \times(3)----(1)$

(4) $3 \mathrm{C}_{(\mathrm{s})}+4 \mathrm{H}_{2(\mathrm{~g})} \rightarrow \mathrm{C}_3 \mathrm{H}_{8(\mathrm{~g})} \quad \Delta \mathrm{H}=103.7 \mathrm{~kJ} / \mathrm{mol}$

(4) is the enthalpy of formation propane $\left(\mathrm{C}_3 \mathrm{H}_6\right)$

Answer = 103.7

Example 3: The enthalpy change for a reaction does not depend on the

1)Physical state of reactants and products.

2)Use of different reactants for the same products.

3) Nature of intermediate reaction steps.

4)Difference in initial or final temperature of involved substances.

Solution

Hess's Law -The total amount of heat change in a chemical reaction is the same whether the reaction is carried out in one or several steps by one or more methods.

$C_{(s)}+O_{2(g)} \rightarrow C O_{2(g)}$

$\Delta H_1=110.5 \mathrm{~kJ}$

$\mathrm{CO}_{(g)}+\frac{1}{2} \mathrm{O}_{2(g)} \rightarrow \mathrm{CO}_{2(g)}$

$\Delta H_2=283.0 \mathrm{~kJ}$

$\Delta H=\Delta H_1+\Delta H_2$

Hess's law of constant heat summation states that regardless of the multiple stages or intermediate steps of the reaction the total enthalpy change for the reaction is the sum of all changes. The enthalpy of a chemical process is independent of the path taken from the initial and the final state.

Hence, the answer is the option (3).

Example 4: The enthalpies of combustion of carbon and carbon monoxide are –393.5 and –283 kJ mol^-1 respectively. The enthalpy of formation (in kJ) of carbon monoxide per mole is

1)110.5

2)676.5

3)-676.5

4) -110.5

Solution

From the concept:

(i) $\mathrm{C}+\mathrm{O}_2 \longrightarrow \mathrm{CO}_2, \Delta \mathrm{H}=-393.5 \mathrm{~kJ} \mathrm{~mol}^{-}$

(ii) $\mathrm{CO}+\frac{1}{2} \mathrm{O}_2 \longrightarrow \mathrm{CO}_2, \Delta \mathrm{H}=-283 \mathrm{~kJ} \mathrm{~mol}^{-}$

Subtracting (ii) from (i)

(iii) $\mathrm{C}+\frac{1}{2} \mathrm{O}_2 \rightarrow \mathrm{CO}, \Delta \mathrm{H}=-110.5 \mathrm{~kJ} \mathrm{~mol}^{-}$

Reaction (iii) represents the formation enthalpy of carbon monoxide.

Example 5: At $25^{\circ} \mathrm{C}$ , the enthalpy of the following processes are given:

$\mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{OH}(\mathrm{g}) \quad \Delta \mathrm{H}^{\circ} \quad=78 \mathrm{~kJ} \mathrm{~mol}^{-1}$

$\mathrm{H}_2(\mathrm{~g})+1 / 2 \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g}) \quad \Delta \mathrm{H}^{\circ}=-242 \mathrm{~kJ} \mathrm{~mol}^{-1}$ $\begin{array}{rrr}\mathrm{H}_2(\mathrm{~g}) & \rightarrow 2 \mathrm{H}(\mathrm{g}) & \Delta \mathrm{H}^{\circ}=436 \mathrm{~kJ} \mathrm{~mol}^{-1} \\ 1 / 2 \mathrm{O}_2(\mathrm{~g}) & \rightarrow \mathrm{O}(\mathrm{g}) & \Delta \mathrm{H}^{\circ}=249 \mathrm{~kJ} \mathrm{~mol}^{-1}\end{array}$

What would be the value of X for the following reaction?

(Nearest integer)

$\mathrm{H}_2 \mathrm{O}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{OH}(\mathrm{g}) \quad \Delta \mathrm{H}^{\circ}=\mathrm{X} \mathrm{kJmol}^{-1}$

1) 499

2)124

3)456

4)210

Solution

$2 \mathrm{H}_2 \mathrm{O}(\mathrm{g}) \rightarrow \mathrm{H}_2(\mathrm{~g})+2(\mathrm{~g})$ & $+(242 \times 2)$
$\mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{OH}$ & +78
$\mathrm{H}_2(\mathrm{~g}) \rightarrow \mathrm{H}_2$ & +436
$2 \mathrm{H}_2 \mathrm{O} \rightarrow 2 \mathrm{H}+2 \mathrm{OH}$ & $+998 \mathrm{KJ} / \mathrm{mole}$
$\mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{H}+\mathrm{OH}$ & $998 \times \frac{1}{2}=+499 \mathrm{KJ} / \mathrm{mole}$

Hence, the answer is (499).

Summary

Hess's Law states that the total enthalpy change of a chemical reaction is the same, regardless of the pathway taken, depending only on the initial and final states. This principle allows for the calculation of reaction enthalpies by summing the enthalpy changes of individual steps, making it especially useful for reactions where direct measurement is challenging. Hess's Law underscores the conservation of energy, as enthalpy is a state function. By using standard enthalpies of formation and combustion, chemists can determine the enthalpy changes of complex reactions. This law is a fundamental tool in thermochemistry, aiding in the understanding and design of chemical processes by providing insights into reaction energetics and enabling accurate energy balance calculations.