Molarity And Mole Fraction: Definition, Formula, Questions

In chemistry, a homogenous mixture of two or more substances in relative amounts can be varied continuously up to what is called the limit of solubility. The term solution is commonly applied to the liquid state of matter, but solutions of gases and solids are possible. Many reactions take place in solutions. In solution generally, one component is present in lesser amounts and is called solute while the other present in access is called solvent.

JEE Main 2025: Chemistry Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics |  PYQs

This Story also Contains

1. Solution:
2. Concentration:
3. Types of concentration terms:
4. Some Solved Examples
5. Conclusion

The concentration of the solution is usually expressed in the following ways: mass percentage or volume percentage, molarity, molality, mole fraction, and normality. In this article, we will cover the concept of reactions in solutions. This topic falls under the broader category of some basic concepts of chemistry which is a crucial chapter in Class 11 chemistry.

Solution:

The solution is a homogeneous mixture of two or more chemically non-reacting substances whose composition can be varied within certain limits.

Solute and Solvent:

The solution is present in the same physical state as that of the solvent.

In case the species forming a solution are all present in the same physical state then the component that is present in a smaller amount is called the solute and the other present in a larger amount is called the solvent.

Concentration:

The concentration of a solution is a measure of the amount of solute that has been dissolved in a given amount of solvent or solution

Types of concentration terms:

(I) Mass fraction or % (w/w)

The mass percentage of a component of a solution is defined as:
Mass % of a component = Mass of the component in the solution Total mass of the solution ×100
For example, if a solution is described as 10% glucose in water by mass, it means that 10 g of glucose is dissolved in 90 g of water resulting in a 100 g solution. Concentration described by mass percentage is commonly used in industrial chemical applications. For example, a commercial bleaching solution contains a 3.62 mass percentage of sodium hypochlorite in water.

Example: A 10 mg effervescent tablet containing sodium bicarbonate and oxalic acid releases 0.25 ml of CO₂ at T = 298.15 K and p = 1 bar. If the molar volume of CO₂ is 25.9 L under such conditions, what is the percentage of sodium bicarbonate in each tablet?
[Molar mass of NaHCO₃ = 84 g mol^-1]

1) 0.84

2) 8.4

3) 16.8

4) 33.6

Solution:

2NaHCO₃+H₂C₂O₄→Na₂C₂O₄+2CO₂+2H₂O

Here, number of moles of CO₂=0.25×10−325.9≈10−5

Now, one mole of CO₂ is produced by one mole of NaHCO₃.

∴ the number of moles of NaHCO₃ in the given reaction
= number of moles of CO₂=10−5

∴% Mass =84×10−510×10−3×100=8.4%

Hence, the answer is (8.4%).

(II) Mole fraction:

The commonly used symbol for mole fraction is x and the subscript used on the right-hand side of x denotes the component.
It is defined as:Mole fraction of a component = Number of moles of the component Total number of moles of all the components

It is expressed by X for example, for a binary solution with two components A and B.

X_A=n_A/n_A+n_B

X_B=n_B/n_A+n_B
X_A+X_B=1

Here n_A and n_B represent moles of solvent and solute respectively. Mole fraction does not depend upon temperature as both solute and solvent are expressed by weight.

(III) Molality

It is the number of moles or gram moles of solute dissolved per kilogram of the solvent. It is denoted by 'm'.m= Weight of solute in gram Molar mass × wt. of solvent in Kg

• If molality is one solution, it is called molal solution.
• One molal solution is less than one molar solution.
• Molality is preferred over molarity during experiments as molality is temperature-independent while molarity is temperature-dependent.

Example: Calculate the molality of a solution containing Acetic acid in Ethanol if the mass of solute = 10g and the density of Ethanol = 0.789 gmL^-1.

1) 0.2112

2) 0.2012

3) 0.1992

4) 0.2002

Solution

We know.

Molality (m) = (number of moles of solute)/(mass of solvent in kg)

Now,

Moles of solute Acetic acid = mass / molar mass

=1060 moles

If Volume of ethanol = 1 L

Formula, Density = mass/volume

So,

Weight of ethanol = 1000 x 0.789 = 789g = 0.789 Kg

Molality = mass of solute mass of solution in kg

Molality =1060×7891000=0.2112 m/kg

Hence, the answer is (0.2112 m/kg).

(IV) Mass by volume percentage (w/V):

Another unit that is commonly used in medicine and pharmacy is mass by volume percentage. It is the mass of solute dissolved in 100 mL of the solution.

(V) Molarity:

It is the number of moles or gram moles of solute dissolved per liter of the solution. Molarity is denoted by 'M'.
M= Weight of solute in gram Molar mass × volume in litre

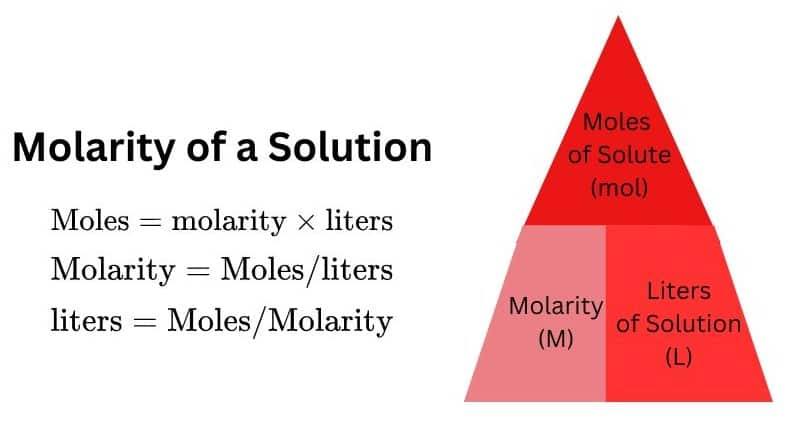
• When the molarity of a solution is one, it is called a molar solution and when it is 0.1, the solution is called a decimolar solution.
• Molarity depends upon temperature and its unit is mol/liter.
• The number of moles of solute if the Molarity and the Volume in liters are given, is calculated as

Moles = M V

In case the volume is given in ml then the millimoles of solute will be given by the above formula

• On dilution water is added and the final volume is made to V₂ , then the moles of solute will remain constant and hence the following formula can be used (V₁ is the volume before dilution, V₂ is the volume after dilution)

M₁V₁ = M₂V₂

• When a mixture of different solutions having different concentrations is taken the molarity of the mixture is calculated as follows: M=M₁V₁+M₂V₂……
• When density and % by weight of a substance in a solution are given, molarity is found as follows:
  M=% by weight ×d×10 Molecular weight
  Here d = density

Example: What volume (in L) of solution of 2M BaSO₄ contains 192 g of SO₄^2- ion?

1) 0.5

2) (correct) 1

3) 2

4) 1.5

Solution

Molarity -

Molarity (M) = (Number of moles of solute)/(volume of solution in litres)

- wherein

It is defined as the number of moles of the solute in 1 liter of the solution.

192 g of SO₄^2- = 2 moles of SO₄^2-

2 moles of SO₄^2- 2 moles of BaSO₄

Volume = no.of moles molarity =22=1L

Hence, the answer is an option (2).

(VI) Normality

It is the number of gram equivalents of solute present in one liter of the solution and it is denoted by 'N'.N= Weight of solute in gram Equivalent mass × volume in litre

• When the normality of a solution is one, the solution is called a normal solution and when it is 0.1, the solution is called a decinormal solution.

Normality Equation:

N₁ V₁=N₂ V₂

• Volume Of water added = V₂ - V₁
  Here V₂ = volume after dilution
  V₁ = volume before dilution
• When density and % by weight of a substance in a solution are given, normality is found as follows:
  
  N=% by weight ×d×10 Equivalent weight
  Here d = density of solution

When a mixture of different solutions having different concentrations is taken the normality of the mixture is calculated as follows: N=N₁V₁+N₂V₂…

(VII) Strength :

It is the amount of solute present in one liter of solution. It is denoted by C or S.
C or S= Weight of solute in gram Volume in litre C=N×E

Here N= normality and E= Eq. wt.

(VIII) The relation between Normality and Molarity :

N = molarity x n-factor

N x Eq wt. = molarity x molar mass

Recommended topic video on (Molarity And Mole Fraction )

Some Solved Examples

Example: A sample of KCl is placed in 50 ml of solvent. What should be the mass (in gm) of the sample for the molarity to be 2M ?

1) 7.45

2) 7.81

3) 6.81

4) 7

Solution

Number of Moles = molarity x volume

= 2 x 0.05 = 0.1

So, mass = (39 + 35.5) x 0.01g = 7.45 g

Hence, the answer is an option (1).

Example: The amount (in g) of sugar (C₁₂H₂₂O₁₁) required to prepare 2L of its 0.1 M aqueous solution is

1) 17.1

2) 68.4

3) 136.8

4) 34.2

Solution

Molarity -Molarity (M) = (Number of moles of solute)/(volume of solution in litres)

It is defined as the number of moles of the solute in 1 liter of the solution.

As we have learned in the mole concept.

The formula of molarity = (n)solute Vsolution ( in lit )

0.1=wt3422

wt(C₁₂H₂₂O₁₁) = 68.4 gram

Hence, the answer is the option (2).

Conclusion

From the discussion of molarity and molality, it is evident that in molarity we consider the volume of the solution while in molality we consider the mass of the solvent. Therefore, the two are never equal. Molality is considered better for expressing the concentration as compared to molarity because the molarity changes with temperature because of the expansion or contraction of the liquid with temperature. However, molality does not change with temperature because the mass of the solvent does not change in temperature.