Quantum Numbers - Principal, Definition, Formula, Applications, FAQs
The quantum numbers determine the behavior of electrons in the atom. They were introduced by the Danish physicist Niels Bohr in 1913 to describe the distinct energy levels of electrons. Later there was another model of the atom which Bohr's Model developed to understand the concept of quantum numbers.
This Story also Contains
- Quantum Number
- Some Solved Examples
- Practice More Questions From the Link Given Below:
- Conclusion
.jpg)
An atom contains a large number of orbitals. These are distinguished from each other on the basis of their size, shape and orientation (direction) in space. These characteristics of an orbital are expressed in terms of three numbers ( Principal, Azimuthal and Magnetic quantum numbers). These numbers also follow from the solutions of schrodinger wave equation. Further to represent the spin of the electron about its own axis, a fourth quantum number, called spin quantum number is introduced.
Quantum Number
We know that large number of orbitals are possible in an atom. Different orbitals have different size, shape and orientation.
Size: Smaller the size of the orbital, more is the chance to be found closer to the nucleus.
Shape and Orientation: It gives the probability of finding the electron more along certain direction.
As various orbitals differ in size, shape and orientation. The above parameters are expressed in terms of different numbers called quantum numbers.
.jpg)
Quantum numbers:
Quantum numbers may be defined as a set of four numbers with the help of which we can get complete information about all the electrons in an atom, i.e., location, energy, the type of orbital occupied, shape and orientation of that orbital, etc. Various quantum numbers are as follows:
- Principal quantum number(n)
- Azimuthal quantum number(l)
- Magnetic quantum number(m)
- Spin quantum number(s)
Also Read:
- NCERT solutions for Class 11 Chemistry Chapter 2 Structure of Atom
- NCERT Exemplar Class 11 Chemistry Solutions Chapter 2 Structure of Atom
- NCERT notes Class 11 Chemistry Chapter 2 Structure of Atom
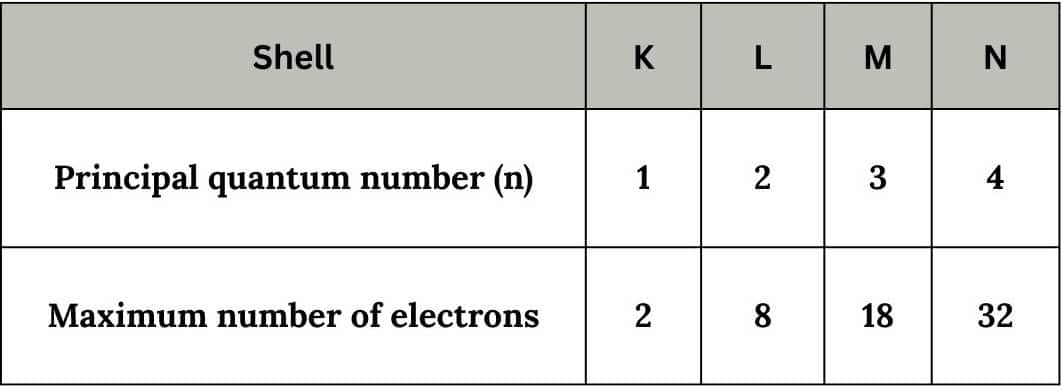
Principal quantum number(n):
It represents the principal shell of an atom. It can have integral values except zero like 1,2,3,.... Also denoted as K,L,M,.....etc.
The maximum number of electrons in a principal shell can be 2n2 where n is the principal quantum number.
This quantum number gives information about :
- Distance of electron from nucleus i.e., size of electron cloud.
- Energy of electron in any shell in unielectronic species
$\mathrm{E}_{\mathrm{n}}=-\frac{1312 \times \mathrm{Z}^2}{\mathrm{n}^2} \mathrm{~kJ} / \mathrm{mol}$
Where Z is the atomic number and n is a principal quantum number.
- In the case of multielectronic species, the energy of an electron is given by Aufbau's Principle, which we shall be studying later.
Azimuthal quantum number(l):
It gives us an idea of the three-dimensional shape of the orbitals.
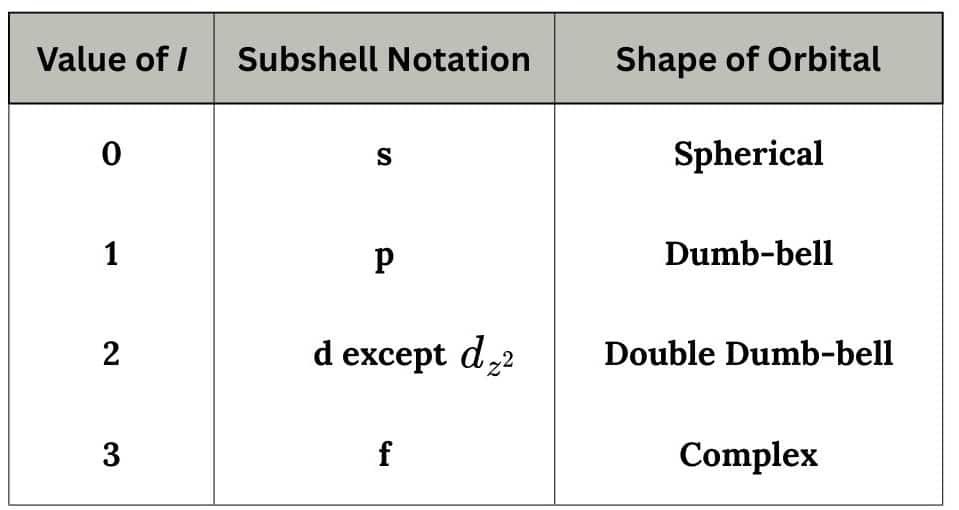
The azimuthal quantum number represents the subshell or sub energy shell in an atom.
l has values from 0 to (n-1).
e.g. for n=2 ; l= 0, 1
Subshell notation for l = 0, 1, 2, ..... is s, p, d ...
A maximum number of electrons that can be accommodated in a subshell with azimuthal quantum number 'l' is given by [2(2l+1)]:
e.g. for s subshell = 2; for p subshell = 6.
The subshells corresponding to different values of 'l' are represneted by the following symbols.
s, p, d, f are the symbols for sharp, principle, diffused, fundamental lines.
.jpg)
Related Topics Link:
- Hydrogen Spectrum
- Atomic number mass number
- Aufbau principle
- Proton Neutron Discovery
- Shapes of Orbitals
- Protons
- Electrons
Magnetic quantum number(m):
It gives us information about the spatial orientation of the orbitals in the subshell concerning the standard set of coordinate axes.
Every value of m represents a possible orientation of the orbital
It represents the number of orbitals present in a subshell.
m has values ranging from -l to +l including zero.
For eg: for ‘s’ subshell :
- Value of l is 0
- m has value=0
It means that there is only one possible orientation for the s orbital.
For ‘p’ subshell :
- Value of l is 1
- m has value= -1, 0, +1
It means that there are three possible orientations for the p-orbital.
.jpg)
Thus, this quantum number explained the splitting of a single spectral line of hydrogen atom into a number of closely spaced lines in the presence of electric (stark effect) and magnetic field (zeeman effect). Because as of now we know that orientations of electrons change in magnetic field leading to the degeneracy of subshells.
Also Read -
- NCERT Solutions for Class 11 Chemistry
- NCERT Solutions for Class 12 Chemistry
- NCERT Solutions for All Subjects
Spin quantum number(s):
An electron in an orbital can spin in either a clockwise or anticlockwise direction. The spin quantum number has no classical analogue and any spin direction can be assigned +1/2 and the opposite spin will be automatically assigned -1/2. These values of +1/2 or -1/2 are not fixed for a particular spin direction.
Thus, an electron can have only two possible values of this quantum number, either $+\frac{1}{2}$ or $-\frac{1}{2}$ respectively.
Recommended topic video on (Quantum Numbers )
Some Solved Examples
Example.1
1. The energy of an electron in a hydrogenic ion depends on:
1) Principal quantum number only
2) Principal and azimuthal quantum numbers only
3) Principal, azimuthal, magnetic quantum number only
4) All four quantum numbers
Solution:
As we learn
Principal Quantum Number -
The principal quantum number determines the size and to a large extent the energy of the orbital.
The energy of hydrogenic ions depends on the principal quantum numbers only.
Hence, the answer is the option (1).
Example.2
Which of the following combination of statements is true regarding the interpretation of the atomic orbitals?
(a) An electron in an orbital of high angular momentum stays away from the nucleus than an electron in an orbital of lower angular momentum.
(b) For a given value of the principal quantum number, the size of the orbit is inversely proportional to the azimuthal quantum number.
(c) According to wave mechanics, the ground state angular momentum is equal to $\frac{h}{2 \pi}$ .
(d) The plot of $
\psi
$ Vs $
r
$ for various azimuthal quantum numbers, shows peak shifting towards a higher r-value.
1) (a), (c)
2) (b), (c)
3) (a), (d)
4) (a), (b)
Solution:
An electron in an orbital of high angular momentum stays away from the nucleus than an electron in an orbital of lower angular momentum.
According to Bohr's theory, angular momentum is an integral multiple of $\mathrm{h} / 2 \pi$. Hence, the ground state angular momentum is equal to $\mathrm{h} / 2 \pi$. But according to wave mechanics, $\frac{h}{2 \pi}$ is wrong because it's $\frac{h}{4 \pi}$.
As we know the principal quantum number depends on size whereas the azimuthal quantum number doesn't depend on size.
Option(d) is also correct, as the plot of $\psi V s r$ shows a peak shifting towards a higher R-value.
Hence, the answer is the option (3).
Example.3
3. The electrons identified by quantum numbers n and l :
(1) n = 4, l = 1 (2) n = 4, l = 0 (3) n = 3, l = 2 (4) n = 3 , l = 1
Can be placed in order of increasing energy as :
1) $(4)<(2)<(3)<(1)$
2) $(2)<(4)<(1)<(3)$
3) $(1)<(3)<(2)<(4)$
4) $(3)<(4)<(2)<(1)$
Solution:
As discussed in the concept
Principal Quantum Number (n) -
It is a positive integer with a value of n = 1,2,3.......
and
Azimuthal Quantum Number(l) -
For a given value of n, l can have n values ranging from 0 to n – 1, that is, for a given value of n, the possible values of l are: l = 0, 1, 2, ....( n –1)
(1) $n=4, l=1 \Rightarrow 4 p$
(2) $n=4, l=0 \Rightarrow 4 s$
(3) $n=3, l=2 \Rightarrow 3 d$
(4) $n=3, l=1 \Rightarrow 3 p$
Increasing the order of energy is
$3 p<4 s<3 d<4 p$
$(4)<(2)<(3)<(1)$
Alternatively,
For (1) $n+l=5 ; n=4$
(2) $n+l=4 ; n=4$
(3) $n+l=5 ; n=3$
(4) $n+l=4 ; n=3$
Lower $n+l$ means less energy and if for two subshells $n+l$
is same than lower n, lower will be the energy.
Thus correct order is (4) < (2) < (3) < (1)
Hence, the answer is the option (1).
Example.4
4. The correct set of four quantum numbers for the valence electrons of the rubidium atom (Z=37) is :
1) $5,0,0,+\frac{1}{2}$
2) $5,1,0,+\frac{1}{2}$
3) $5,1,1,+\frac{1}{2}$
4) $5,0,1,+\frac{1}{2}$
Solution:
We know that -
Principal Quantum Number (n) -
It is a positive integer with a value of n = 1,2,3.......
Azimuthal Quantum Number(l) -
For a given value of n, l can have n values ranging from 0 to n – 1, that is, for a given value of n, the possible values of l are: l = 0, 1, 2, ....( n –1)
Magnetic Quantum Number (m) -
For any sub-shell (defined by ‘l ’value) $2 l+1$values of m are possible and these values are given by :
m = – l , – ( l –1), – ( l – 2)... 0,1... ( l – 2), ( l –1),l
Spin Quantum Number (s) -
It has two values +1/2 and -1/2
${ }_{37}^{R b}=>1 S^2, 2 S^2, 2 p^6, 3 S^2, 3 p^6, 4 S^2, 3 d^{10}, 4 p^6, 5 S^1$
the value of n, l, m & s for the last electrons are
$5,0,0,+\frac{1}{2}$
Hence, the answer is an option (1).
Example.5
5. The quantum number of four electrons is given below:
$\begin{aligned} & I . n=4, l=2, m_l=-2, m_s=-1 / 2 \\ & \text { II.n }=3, l=2, m_l=1, m_s=+1 / 2 \\ & \text { III.n }=4, l=1, m_l=0, m_s=+1 / 2 \\ & \text { IV.n }=3, l=1, m_l=1, m_s=-1 / 2\end{aligned}$
The correct order of their increasing energies will be :
1) $I<I I<I I I<I V$
2) $I V<I I I<I I<I$
3) $I V<I I<I I I<I$
4) $I<I I I<I I<I V$
Solution:
| n | l | n+l | ||
| 1 | 4 | 2 | 6 | 4d |
| 2 | 3 | 2 | 5 | 3d |
| 3 | 4 | 1 | 5 | 4p |
| 4 | 3 | 1 | 4 | 3p |
The higher the value of ($n+l$) the higher will be the energy.
If two orbitals have the same value of (n+l), the orbital with the higher value of n will have higher energy.
So, order will be => IV < II < III < I
Hence, the answer is the option (3).
Practice More Questions From the Link Given Below:
Conclusion
Quantum numbers are very useful in determining the properties of electrons in atoms. They define the energy levels, arrangement of atoms in the space or spatial arrangement, and spin orientation of electrons. Quantum numbers describe the number of energy levels or shells of electrons. It also determines the size and energy of the orbital. quantum numbers provide a comprehensive of an electron's state within an atom, including its energy, spatial arrangement, and its magnetic properties
Also Check-
- NCERT Exemplar Class 11th Chemistry Solutions
- NCERT Exemplar Class 12th Chemistry Solutions
- NCERT Exemplar Solutions for All Subjects
NCERT Chemistry Notes:
Frequently Asked Questions (FAQs)
Simply put, it is physics that explains how everything works: the best explanation we have for the type of particles that make up a matter and the forces they encounter.
Einstein saw Quantum numbers as a means of explaining nature at the atomic level, but doubted it supported "a practical foundation for all physics." He reasoned that explaining the truth required strong predictions followed by positive forecasts.
Einstein first contributed to quantum numbers by including his suggestion that light behaves as if it is made up of photons, as well as his exploration of the quantum structure of the mechanical force of particles embedded in matter.
The basis of quantum equipment is the Heisenberg uncertainty system. ... Physics students are still being taught this version of the equation-disruption system of uncertainty in presentation classes, but it turns out that it is not always true.
Schrodinger's cat was not a real experiment, so it did not prove anything scientifically. Schrodinger his attempt to think of a cat to show that a vague interpretation of quantum numbers could lead to absurd results that are incompatible with the real world.