COT Full Form
What is the Full Form of COT?
One of the six trigonometric functions is the cotangent. Typically, it is referred to as a "COT." It is, in reality, one of the CSC, SEC, and COT reciprocal trigonometric ratios where CSC means cosecant, and SEC means secant. It is typically written as "cot x," where x is the angle formed by a right-angled triangle's base and hypotenuse. Cotangent also goes by the names cotan and cotangent x. The ratio of the adjacent side (the side next to the angle) to the opposing side (the side opposite to the angle) is known as the cotangent of an angle in a right triangle.
Formula For COT
The formula of Cotangent is
\mathrm{Cot \theta} = \frac{\text{adjcent side}}{\text{Opposite side}}
Consider the right-angled triangle ABC, which is right-angled at B. The side next to A is then AB, while the side opposite A is BC. Consequently, the cotangent of A (also known as cot A) is:
\begin{aligned}
&\operatorname{Cot} \theta=\frac{\text { adjcent side }}{\text { Opposite side }} \\
&\operatorname{Cot} \mathrm{A}=\frac{\text { adjcent side of } \mathrm{A}}{\text { Opposite side of } \mathrm{A}} \\
&\operatorname{Cot} \mathrm{A}=\frac{A B}{B C}
\end{aligned}
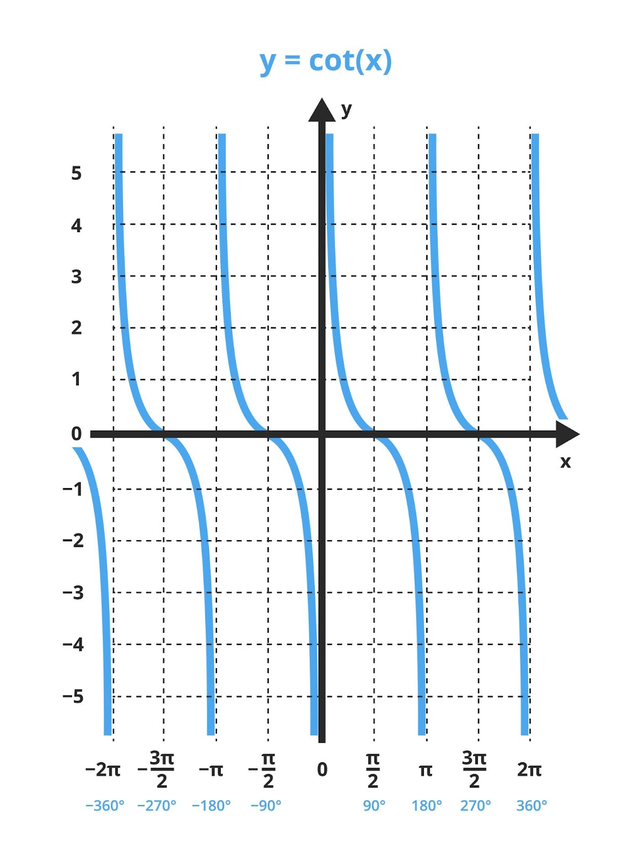
The graph of Function COT(x) vs x (angle)
Trigonometry Ratios Of COT
Angles in degrees | 0 | 30 | 45 | 60 | 90 |
COT(X) |
\infty |
\sqrt{3} | 1 |
| 0 |
\frac{1}{\sqrt{3}}Trigonometric Identities Of COT-
\mathrm{Cot A} =\frac{\mathrm{Cos A}}{\mathrm{Sin A}}.
\mathrm{Cot A} =\frac{\mathrm{1}}{\mathrm{Tan A}}.
\mathrm{Cot A} =\frac{\mathrm{Cosec A}}{\mathrm{Sec A}}
Frequently Asked Questions (FAQs)
The set of real numbers, except all the integer multiples of \pi 
, constitutes the domain of cotangent.
The set of all real numbers is the cotangent's range.
The cotangent of A is defined to be the cosine of A divided by the sine of A:
\mathrm{Cot ( 90- \theta)} =\mathrm{Tan \theta}.
The Pythagorean identity of COT A is \mathrm{Cot^{2} A} = \mathrm{CSC^{2} A} -1
The derivative of COT is \frac{d}{{dx}}\cot x = - \csc ^2 x
All multiples of \pi 
have vertical asymptotes for the cotangent function.