How to Find Prime Numbers in Python?

A prime number is a whole number with only two positive factors: 1 and itself. The first five prime numbers are 2, 3, 5, 7, and 11. Kindly note that 1 is not a prime number. In addition to mathematics, computer science is a field where prime numbers are used on a large scale, specifically in Cryptography, calculating Hash Codes, and other algorithms.

Latest: Python for Beginners: Top Certification Courses and prerequisites

In this article, we will provide you with easy demonstrations of a Python program to find whether a number is prime or not. If you are interested in gaining further knowledge in this domain, you can also go through the list of Online Python Courses and Certifications listed on the Careers360 website.

Also Read:

• A Beginner's Guide to Pursue Python Programming
• 10 Python Courses For Aspiring Data Scientists
• Fibonacci Series in Python: A Step-By-Step Guide

Python Program for Prime Number

There are “n” number of ways to write Python code to check prime numbers. You can use recursion, a flag variable, a division method, or loops to find out whether the given number is prime or not. In this section, we will cover both basic and optimised methods for this task.

Basic Method:

num = int(input("Enter Your Number:"))

print(num)

for i in range(2, num):

if num % i == 0:

print("Your number is not Prime")

break

else:

print("Your Number is Prime")

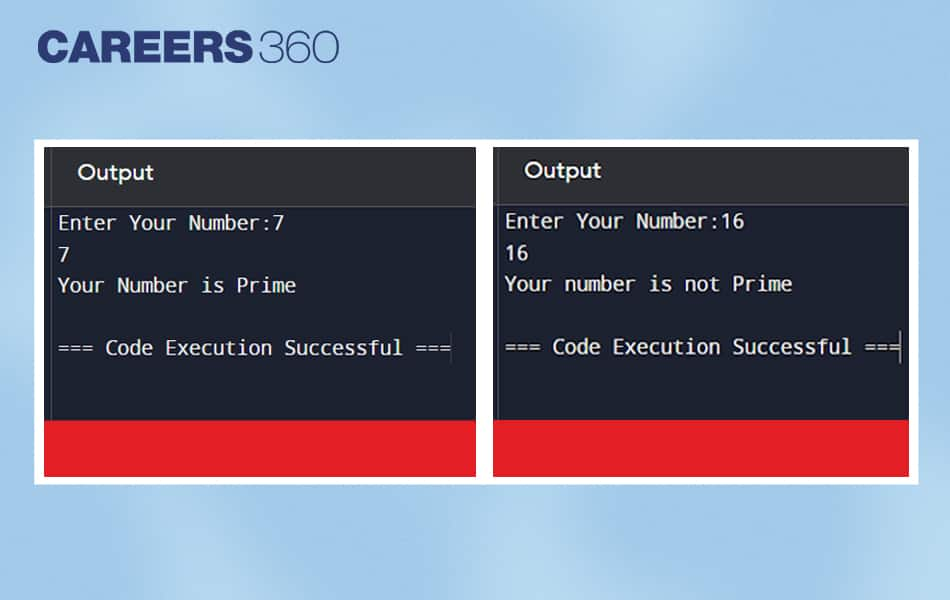
Images showing the output of the code for two different input

Code Explanation

• In the first line of code, we have taken a ‘num’ variable to store the input provided by the user. The ‘input()’ function is used to take input in Python language and the ‘int()’ function converts the input (which is a string) to an integer and assigns it to the variable ‘num’.
• The second line will simply print the number entered by the user.
• Now, the ‘for’ block is where the number is logically tested to find whether it is prime or not.
• Because 2 is the first prime number, we will start our iteration from 2 which will range up to ‘num’.
• Inside the loop, the ‘if' statement checks if ‘num’ is divisible by ‘i' using the modulus operator ‘%’.
• If ‘num’ is divisible by ’i' (which means, there is no remainder), ‘num’ is not a prime number.
• It will print "Your number is not Prime", and the ‘break’ statement exits the loop immediately.
• If the loop completes without finding any divisors (no break is encountered), the else block is executed and it will print "Your Number is Prime".

Code Problem:

We can see this prime number code working well for most cases, but do you think this is efficient and will work for all scenarios? No, it will not. In this code, we have provided a range starting from 2.

But what if the user enters the input like 1, 0, or any other negative number? For these inputs also, this prime number code will perform well? Have a look at the below-provided output images.

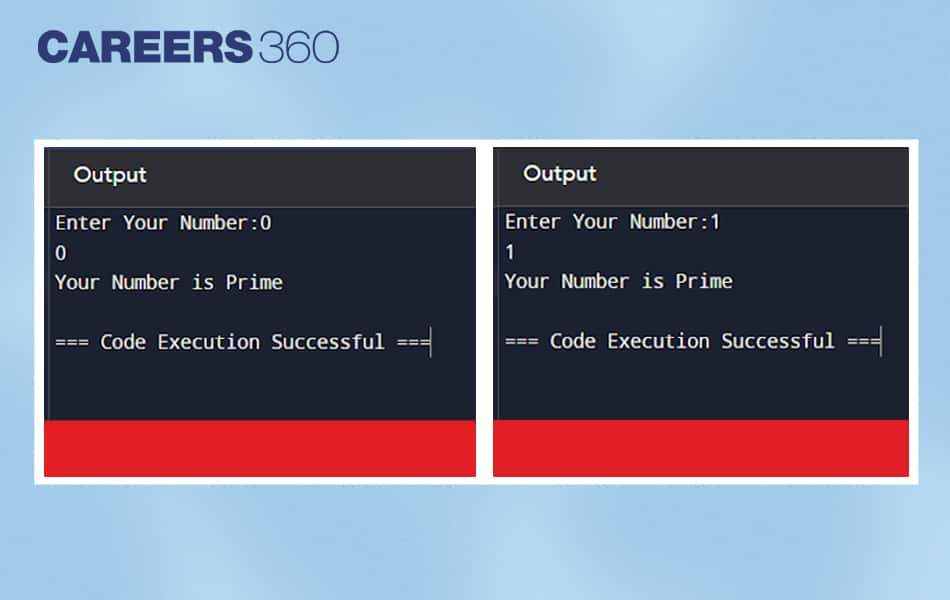
Images showing the output of the inputs 0 and 1

As you can see, the output of the inputs 0 and 1 is not what we desired because, neither 0 is a prime number nor a 1. To tackle this problem, in the following section of the article, we have provided an optimised code solution.

Optimised Method

num = int(input("Enter Your Number:"))

print(num)

import math

def prime_function(num):

if num<=1:

return False

for i in range(2, int(math.sqrt(num))+1):

if num % i == 0:

return False

return True

if prime_function(num):

print("Your number is Prime")

else:

print("Your Number is not Prime")

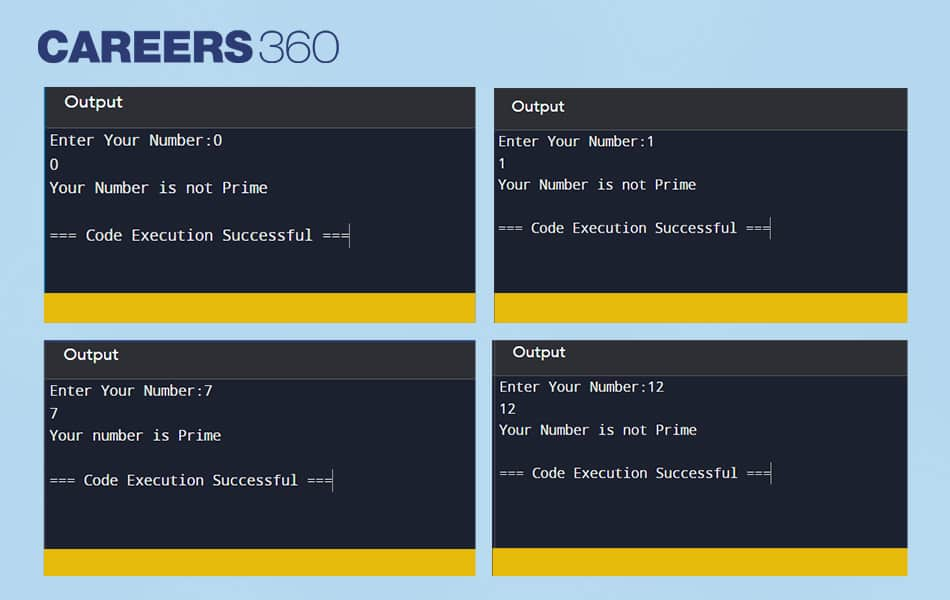
Image showing output for different inputs entered by the user by compiling above-mentioned program

Code Explanation

The first thing to understand is that the factor of number will never be greater than half of that number. Therefore, instead of considering a range up to the ‘num’ itself, we can limit the range to num // 2 + 1. To optmise it more, we can use an in-built Python module called ‘math’.

• The third line of the code will import the ‘math’ module of Python that provides access to various mathematical functions.
• The fourth line defines a function named ‘prime_function’ that takes a single parameter ‘num’.
• The ‘if' statement checks if the number is less than or equal to 1. If it is, the function returns False because 1 and any number less than 1 are not prime.
• The ‘for’ loop iterates from 2 to the square root of num (inclusive). The square root is used to reduce the number of iterations because a larger factor of the number must be a multiple of a smaller factor that has already been checked.
• ‘if num % i == 0’ will check if ‘num' is divisible by ‘i'. If it is, the function returns False because ‘num’ is not prime.
• If no divisors are found, the next line will return True and indicate that 'num' is prime.
• ‘if prime_function(num)’ line calls the ‘prime_function’ with ‘num’ as an argument. If the function returns True, the following block is executed.

Also Read:

• All You Need to Know About Object Oriented Concepts in Python
• Understanding the _init_ Function In Python
• Free Python Courses & Certifications

The Significance of Prime Numbers

The prime number code in Python can be applied in various scenarios. Whether you need to identify prime numbers for cryptography, number theory, or other mathematical applications, this prime no program in Python will be a valuable tool in your toolkit.

Cryptography: Prime numbers are at the core of modern cryptography. They play a crucial role in securing data and provide the basis for encryption and decryption algorithms.

Random Number Generation: Prime numbers are often used to generate pseudo-random numbers in computer programs, simulations, and games. These random numbers are required for initialisation vectors and for generating private and public keys.

Optimisation Algorithms: In various optimisation problems, prime numbers can be used to create unique solutions.

Number Theory: The branch of mathematics that shows the number and the relation between them is called ‘number theory’. Prime numbers are important to number theory as they are used in digital signatures, error correction, and hashing.

Related: Python Certification Courses by Top Providers

• edX Python Certification Courses
• Google Python Certification Courses
• Udemy Python Certification Courses
• Coursera Python Certification Courses
• Futurelearn Python Certification Courses
• Futureskills Python Certification Courses
• Mindmajix Technologies Python Certification Courses
• Raspberry Pi Foundation Python Certification Courses

Conclusion

Prime number program in Python is one of the basic and yet considered an important concept for advanced topics like number theory or cryptography. In this guide, we have covered the definition of prime numbers, a basic method for checking prime numbers, and an optimised method to make the process more efficient.

Other than the above-discussed ways of finding whether a number is prime or not in Python, there are many other techniques. You can practice the given code to enhance your understanding and even modify it according to your logic.