CPK Full Form
What is the full form of CPK?
CPK stands for Process Capability index.It is a measure of process capability. It helps us to know how close we are to achieving our goals and how consistent our performance is. process capability index always calculates the best scenario for our current procedure.
What is CPK
CPK process capability index is very popular among those people who want to estimate the output of the product that they are manufacturing.It helps them to manufacture estimating,, manage the resources and potential production to get best results.collected data are frequently use as inputs for CPK it is generally used when a procedure is under statistical control (statical control is a method to monitor,measurer and also control a process)
Formula of CPK
Below down there is a formula of process capability index:
\begin{equation}
C p k=\min \left(\frac{U S L-\text { mean }}{3 \sigma}, \frac{\text { mean }-L S L}{3 \sigma}\right)
\end{equation}
Where, USL means upper specification limits.
LSL means lower specification limits.
, is standard deviation.
Values of CPK
1.If the value of CPK is equal to value of CP(process capability) then the process is functioning on edge.
2. If CPK is less than 0 then the process has violated one of important boundaries.It not a good sign.
3.When CPK is larger than 0 but less than 1 then the process is within important limits but a portion of manufacturing output has exceeded them.
4.If CPK is bigger than 1 then the process is completely centred and within the specification limits.It is a good sign.
Frequently Asked Questions (FAQs)
If the value of CPK is equal to 1.33 then the process is capable and also meets the specification limits.
When CPK is negative it indicates that the process will produce output that is not under the customer specification limits.
No, CPK can never be larger than CP(process capability)
Yes, if the processes are producing the same product dimension then you can compare them.
The value of cpk is
The upper specification limit is 32 ounces whereas the lower specification limit is 20 ounces.
\begin{equation}
\begin{aligned}
& \text { Cpk = Min } \frac{(30-27)}{7} \text { or } \frac{(27-20)}{7} \\
& =\min \text { of } \frac{3}{7} \text { or } \frac{7}{7} \\
& =0.43 \text { or } 1
\end{aligned}
\end{equation}
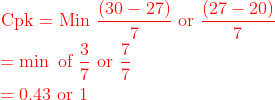
Since, the minimum value is 0.43 then the process capability index is 0.43.