GP Full Form

What is the full form of GP?

The full form of GP is Geometric Progression. Numbers that are organized in a certain order to create a predictable order are known as progressions (also known as sequences and series). Predictable order refers to the ability to anticipate the following numbers in a series given a set of numbers. A mathematical sequence known as a geometric progression (GP) is one in which each following term is generated by multiplying each preceding term by a fixed integer, or "common ratio." Here, each term is multiplied by the common ratio to generate the subsequent term, which is a non-zero value. A geometric series with a common ratio of 3 is 1, 3, 9, 27, etc.

This Story also Contains

1. What is the full form of GP?
2. Definition of geometric progression (GP)
3. Properties of geometric progression
4. General form of GP
5. Types of geometric progression
6. Sum of the nth term of a finite GP

Definition of geometric progression (GP)

When one term is varied by another by a common ratio, the series is referred to as a geometric progression or sequence. When we multiply the previous term by a constant called the common ratio (which is non-zero), we get the next term in the series. The Geometric Progression can be represented as:

a, ar, ar^2 , ar^3, ar^4,....., a{r^{n - 1}}.

Where a is the first term of GP and r is the common ratio.

The common ratio is given by dividing any term by the previous term. Let’s divide the second term by the first term and the third term by the second term.

\frac{{ar}}{a} = \frac{{a{r^2}}}{{ar}} = r

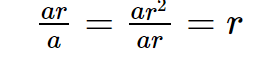
Properties of geometric progression

There are various properties of geometric progression which help us to solve various types of problems that include geometric progression. Some properties are as follows:
If the three numbers a, b, and c are in GP, then they must satisfy \[{b^2} = ac\].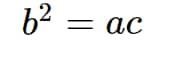

2. The product of the terms that are equally distant from the beginning and the end is the same in a finite GP.
   {t_1} \cdot {t_n}\; = {\rm{ }}{t_2} \cdot {t_{n - 1}}\; = {\rm{ }}{t_3} \cdot {t_{n - 2}}\; = {\rm{ }} \ldots ..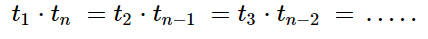
   

3. When a GP is multiplied or divided by a non-zero constant, the new sequence is also a GP with the same common ratio.

4. If we multiply or divide two geometric progression, then the resulting sequence is also a GP.

5. When each term of a GP is raised to the power of the same non-zero quantity, then the new sequence is also a GP.

6. log a1, log a2, log a3,... is an AP (arithmetic progression) if a1, a2, a3,... is a GP of positive terms and vice versa.

7. The three consecutive terms of a GP can be written as \frac{a}{r},{\rm{ }}a,{\rm{ }}ar.

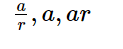
General form of GP

The basic configuration of a geometric progression is as follows:

a,ar,a{r^2},a{r^3}.....a{r^{n - 1}}

Where “a” is the first term of geometric progression, “r” is the common ratio and a{r^{n - 1}} is the last term.

Common Ratio And nth Term Of a GP

The geometric progression with “a” as the first term and “r” as the common ratio is given as

a,ar,a{r^2},a{r^3}.....a{r^{n - 1}}

The common ratio is the ratio of any term to its previous term. If we want to find the common ratio, then we divide the fourth term by the third term or the second term by the first term, or the last term by the second last term.

\begin{array}{l}r = \frac{{{a_n}}}{{{a_{n - 1}}}} = \frac{{a{r^{n - 1}}}}{{a{r^{n - 2}}}}\\ \end{array}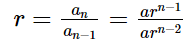

The nth term of a GP is given by,

{a_n} = a{r^{n - 1}}

By using the general term we can find any term of a geometric progression if the first term and common ratio of GP are known.

Let's suppose a student wants to find the fourth term of a GP with 3 as the first term and 2 as a common ratio, so

Putting the values,

\begin{aligned}

&a_n=a r^{n-1} \\

&a_4=3 \times 2^{4-1} \\

&=3 \times 8 \\

&=24

\end{aligned}

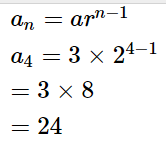
Hence, 24 is the fourth term of the given GP.

Types of geometric progression

Based on the number of terms it contains, geometric progression can be classified into two categories.

1. Finite Geometric Progression
   The finite geometric progression is a sequence with a finite number of terms. The geometric progression with “a” as the first term and “r” as the common ratio has finite terms and is given as
   a,ar,a{r^2},a{r^3}.....a{r^{n - 1}}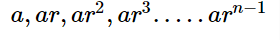
   The above GP is an example of finite geometric progression.

2. There are an infinite number of terms in an infinite geometric progression. It is a progression in which the last term is not defined.

An example of an infinite geometric progression is given below

3,6,12,24,.......

Sum of the nth term of a finite GP

The following is the geometric progression with “a” as the first term and “r” as the common ratio:

a,ar,a{r^2},a{r^3}.....a{r^{n - 1}}

The sum of the nth term of the above-given GP is given by,

{S_n} = \frac{{a({r^n} - 1)}}{{r - 1}}

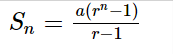
Where the common ratio r ≠ 1 and r > 1.

If the common ratio is 1, then the sum up to nth term is given by,

{S_n} = na

The sum of infinite Geometric progression is given by the formula S_\infty = \frac{a}{1 - r}.

Solved Examples Of Geometric Progression

1. Write the first three terms of a GP if the first term is 4 and the common ratio of a GP is 2.

Ans. The first term is 4 and the common ratio is 2, so using the general term of GP,

\begin{aligned}

&a_n=a r^{n-1} \\

&a_1=4 \times 2^{1-1} \\

&a_1=4 \\

&a_2=4 \times 2^{2-1} \\

&a_2=8 \\

&a_3=4 \times 2^{3-1} \\

&a_3=16

\end{aligned}

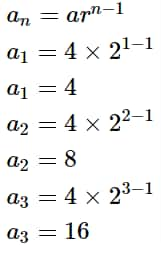
Hence, the first three terms are 4, 8, and 16.

2. Find the 13th term of GP: 10, 30, 90, 270 ….

Ans. Here the first term is 10, so a=10.

The common ratio will be \frac{{30}}{{10}} = 3

Now, the 13th term is given by putting n=13 in the general term of GP,

\begin{aligned}

&a_n=a r^{n-1} \\

&a_{13}=10 \times 3^{13-1} \\

&a_{13}=10 \times 3^{12} \\

&a_{13}=5314410

\end{aligned}

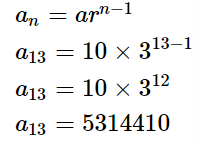
3. Find the total sum of the following numbers: 32, 16, 8, 4,..., till infinity.

Ans. Here the first term is 32, so a=32.

The common ratio will be \frac{{16}}{{32}} = \frac{1}{2}.

Now, put the value of the first term and common ratio in the formula of the sum of n terms.

\begin{aligned}

&S_n=\frac{a}{1-r} \\

&S_n=\frac{32}{1-0.5} \\

&S_n=\frac{32}{0.5} \\

&S_n=32 \times 2 \\

&S_n=64

\end{aligned}

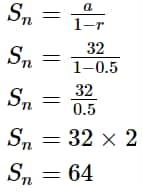
4. Find the total sum of these infinite geometric progression's terms: \frac{1}{3},\frac{1}{9},\frac{1}{{27}},.....\infty .
   

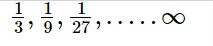
Ans. Here the first term is \frac{1}{3} , so a = \frac{1}{3} .

The common ratio will be \frac{{\frac{1}{9}}}{{\frac{1}{3}}} = \frac{1}{3} .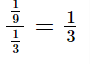

Now, put the value of the first term and common ratio in the formula of the sum of n terms.

\begin{aligned}

&S_n=\frac{\frac{1}{3}}{1-\frac{1}{3}} \\

&S_n=\frac{\frac{1}{3}}{\frac{3-1}{3}} \\

&S_n=\frac{1}{3} \times \frac{3}{2} \\

&S_n=\frac{1}{2}

\end{aligned}

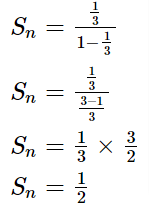
5. Check whether the terms -1, 2, and -4 are in geometric progression or not.

Ans. We know that if three numbers are in GP then they must satisfy {b^2} = ac .

So, putting the values and checking,

\begin{array}{l}{2^2} = ( - 1)( - 4)\\4 = 4\end{array}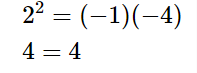

Hence, LHS=RHS

So the given terms -1, 2, -4 are in GP.