H2, P2, B2 Full Form
What is the full form of h2, p2, b2?
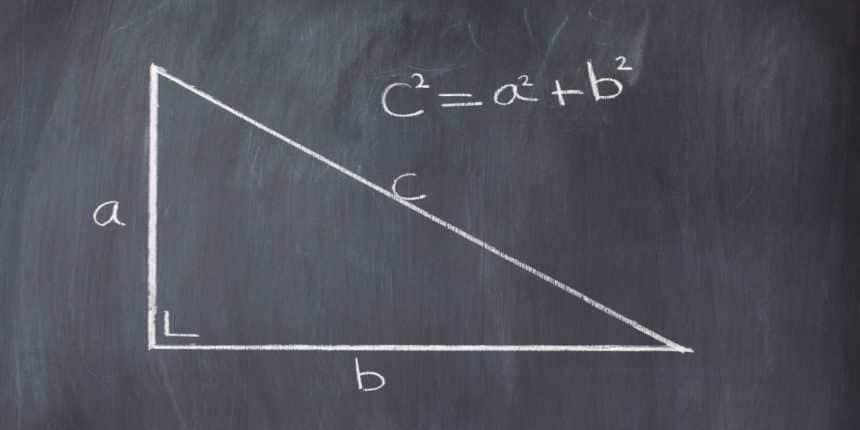
Pythagoras' theorem in mathematics is a theorem which defines the relation between sides of a right-angle triangle and is also used to find missing sides of a triangle. It is named after the greek philosopher Pythagoras, and the formula is:
h2 = p2 + b2
Where:-
h stands for the hypotenuse
p stands for perpendicular
b stands for base
- What is the full form of h2, p2, b2?
- Defining hypotenuse, perpendicular, and base:-
- Derivation of pythagoras theorem: h2 = p2 + b2
- Examples
In this article, first, we would break down the Pythagorean theorem and then take a deep dive into understanding where they came from. In the end, we would see some examples to understand the terms.
Defining hypotenuse, perpendicular, and base:-
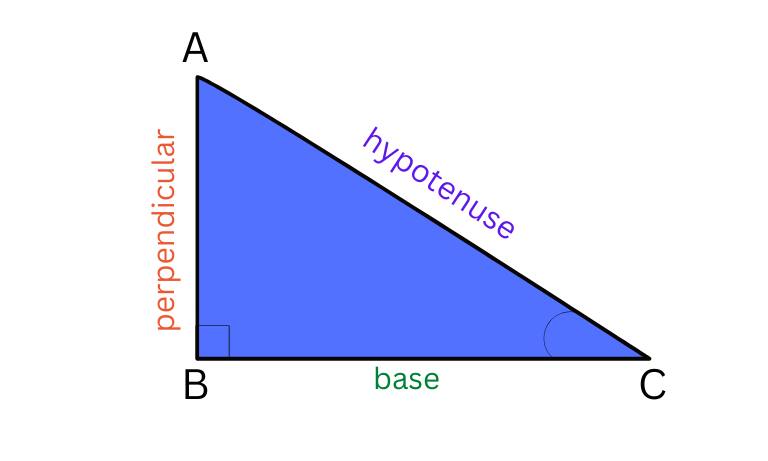
Hypotenuse: (AC) The opposite line of the right angle, which is the longest, is called the hypotenuse.
Perpendicular: (AB) The straight verical line at the angle of 90 degrees is called perpendicular. If we give reference to one of the acute angles, then it is the line opposite to the angle.
Base: (BC) The line where the perpendicular AB stands is called the Base. When referring to a particular acute angle, this is the line on which angle is formed with the hypotenuse.
Derivation of pythagoras theorem: h2 = p2 + b2
Let us take a square with sides PQSR
Where PQ is divided into two parts: a and b
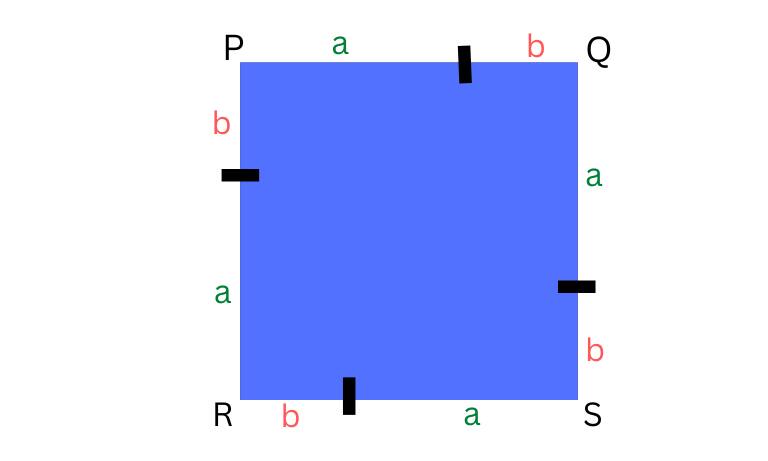
As it is a Square, hence PQ = QS = SR = RP = (a+b)
Now, connect the lines that divided a’s and b’s
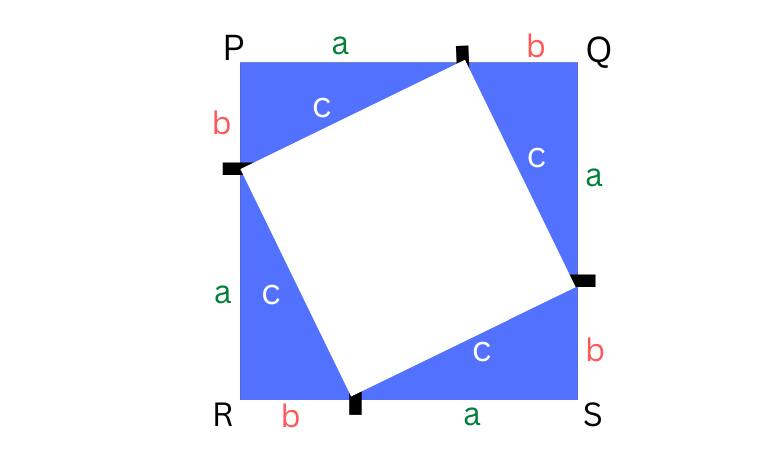
In the diagram above, we can see that four triangles are formed
Let us calculate the area of PQSR (bigger square)
Area of the bigger square = Area of four triangles + Area of small square
\begin{aligned}
&(a+b)^2=4\left(\frac{1}{2} a b\right)+c^2 \
&a^2+2 a b+b^2=2 a b+c^2 \
&a^2+b^2=c^2
\end{aligned}
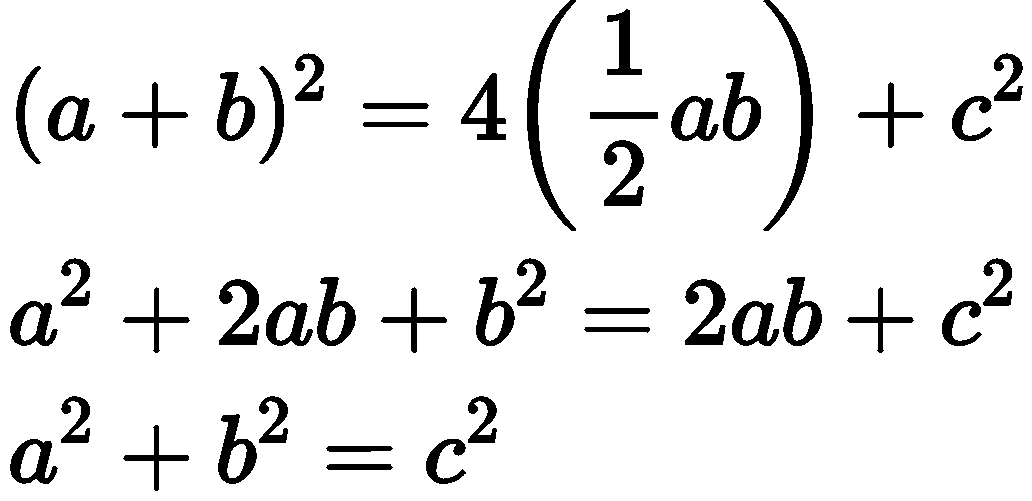
Hence Proved.
Examples
Q1) A triangle ABC has a base of 6 cm and a perpendicular is 10 cm. Find the hypotenuse
Ans: First, we will arrange the numbers as follows:
h = ?
p = 10 cm
b = 6 cm
On putting the formula, we get:
\begin{aligned}
&h^{2}=10^{2}+6^{2}\
&=h=\sqrt{136}\
&=h=11.66cm
\end{aligned}
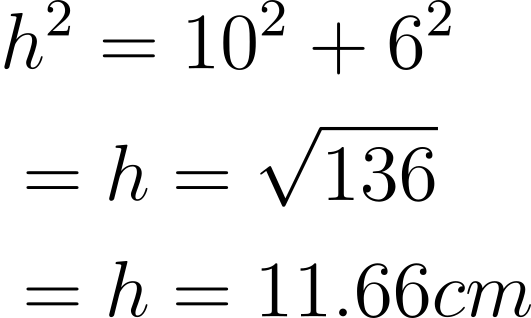
Q2) A triangle LMN has a base of 4 cm hypotenuse is 8 cm, find the perpendicular.
Ans: h = 8 cm
p = ?
b = 4 cm
On putting the formula, we get:
\begin{aligned}
&p^{2}=8^{2}-4^{2}\
&=p=\sqrt{46}\
&=p=6.78cm
\end{aligned}
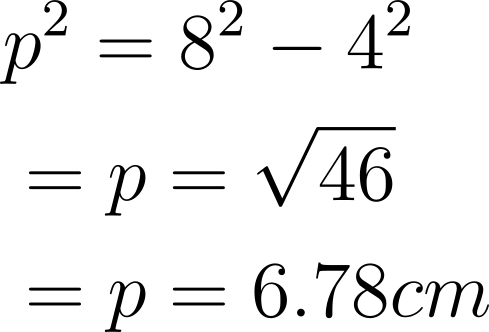
Q3) A triangle XYZ has a perpendicular of 36 cm and hypotenuse of 90 cm, find the base
Ans: h = 90 cm
p = 36
b = ?
On putting the formula, we get:
\begin{aligned}
&b^{2}=90^{2}-36^{2}\
&=b=\sqrt{6804}\
&=b=82.48cm
\end{aligned}
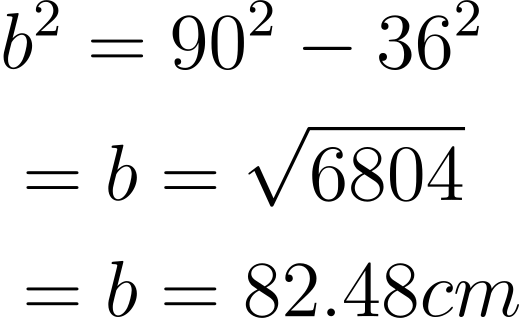
Frequently Asked Questions (FAQs)
No, Pythagoras' theorem is only used for right-angle triangles.
They are used for:
Construction and architecture
Calculating the slope of hills or mountains
Finding the length of a tree that has been broken down and fallen
According to historians, the first person to prove Pythagoras' theorem was an ancient Indian mathematician Baudhayan, who lived around 800 BCE.
Hypotenuse is the longest length compared to perpendicular and base.
Pythagoras' theorem can be proven in many ways, but here are a few ways:
Algebraic proofs
Proof using similar triangles
Euclid's proof
Proofs by dissection and rearrangement
Proof using differentials
