HCF and LCM Full Forms
From the first impression, it is evident that “HCF” and “LCM” are acronyms. You will here, learn the full forms of “HCF” and “LCM”, and also their functionalities. Before you gather from here, how to find the “HCF” and “LCM” of numbers, first you have to realize what are meant by “factors” and “multiples” of a number.
As such, you are acquainted with the multiplication tables. Every multiplication table is, basically, the table involving the “factors” and “multiples” of numbers. Among these “factors” and “multiples” of numbers, you will find some “common factors” and “common multiples”. Isn’t it right? Let us dive into it to explore further.
What Is A “Factor”?
Look at this mathematical expression.
\[6000={{2}^{4}}\times 3\times {{5}^{3}}\]
![]()
Note that “6000” is completely divisible by “2”.
\[6000\div 2=3000\]
![]()
So, what you call “2” is a factor of “6000”.
Similarly, you have the following factors of “6000”.
\[\text{Factors of 60}00=\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 8,\ 10,\ \ldots \ 6000\]
![]()
Thus, you get that when an integer divides a number completely without leaving any remainder, you call that integer the “factor” of the number.
What Is A “Multiple”?
Observe this multiplication table of “12”.
\[\begin{align}
12\times 1=12 \\
12\times 2=24 \\
12\times 3=36 \\
12\times 4=48 \\
12\times 5=60 \\
\end{align}\]
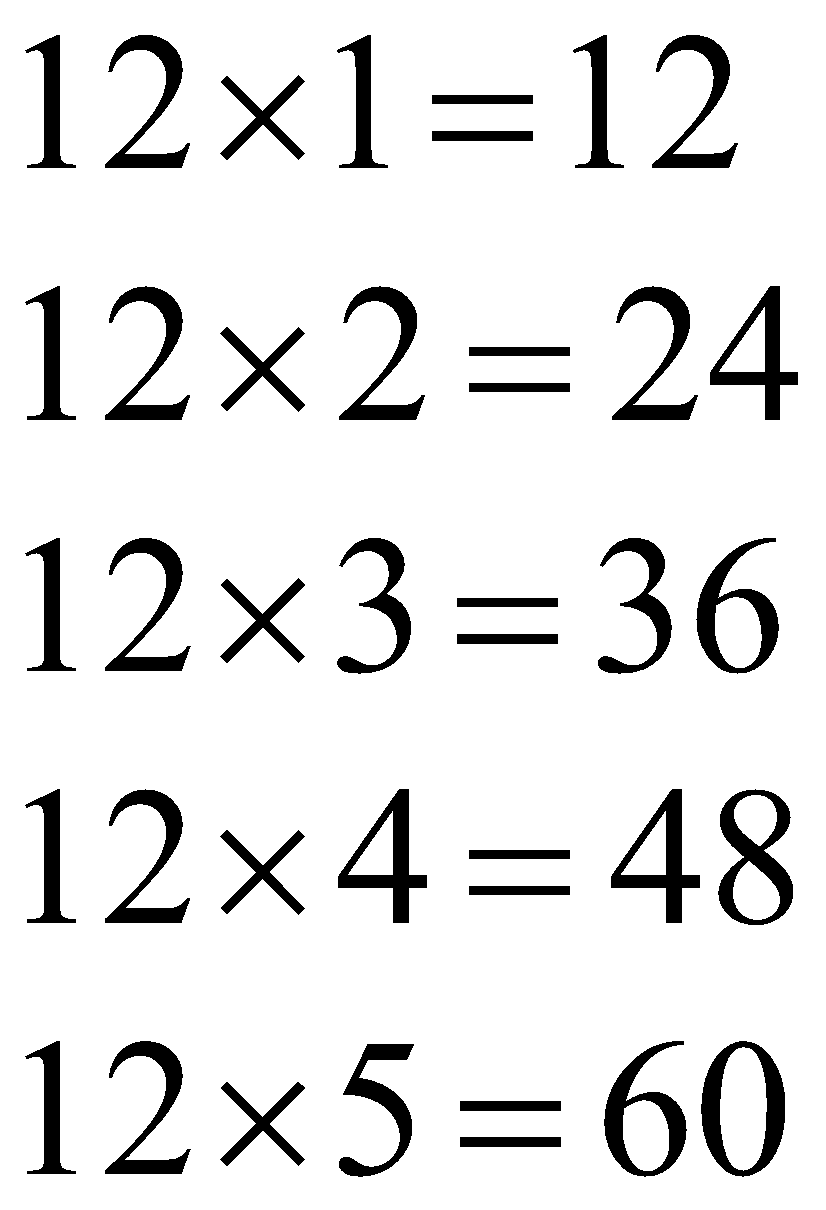
Note that the numbers ![]()
![]() are “multiples of 12” as you get them by multiplying “12” with
are “multiples of 12” as you get them by multiplying “12” with ![]()
![]() respectively.
respectively.
Thus, you will obtain an indefinite number of “multiples of 12” as you continue to increase the value of the multiplier of “12”.
What is the full form of “HCF”?
In the abbreviation “HCF”, the letter “H” stands for “Highest”, the letter “C” stands for “Common”, and the last letter “F” stands for “Factor”.
Go through this example to understand what this “Highest Common Factor” means.
Suppose, you have the three numbers “20”, “60”, and “100”; and you have the following observations.
\[\begin{align}
\text{Factors of 2}0\quad =\ 1,\ 2,\ 4,\ 5,\ 10,\ 20 \\
\text{Factors of 6}0\quad =\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 10,\ 12,\ 15,\ 20,\ 30,\ 60 \\
\text{Factors of 10}0\ =\ 1,\ 2,\ 4,\ 5,\ 10,\ 20,\ 25,\ 50,\ 100 \\
\end{align}\]
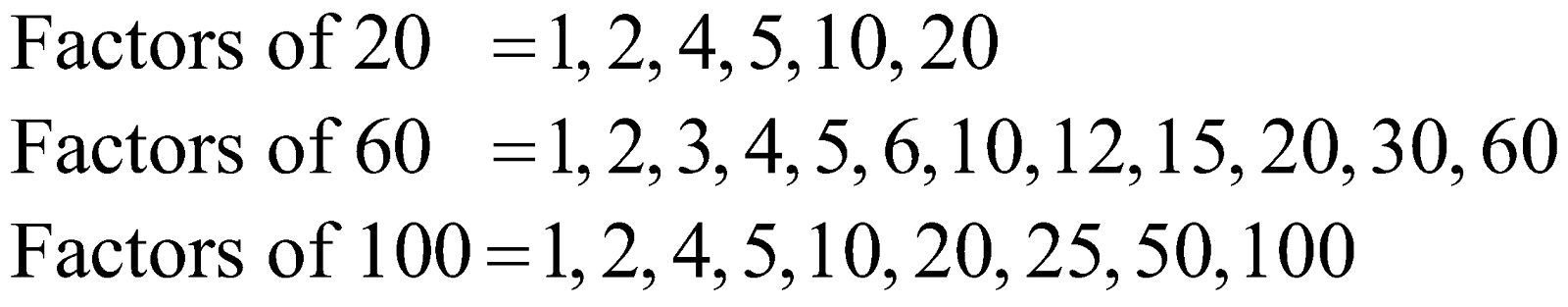
Here, the “common factors” of “20”, “60”, and “100” are ![]()
![]()
![]()
Note that among these “common factors”, it is clear that “20” is the “Highest Common Factor” of “20”, “60”, and “100”. The method employed here to find “HCF” is “Factorization”.
Again, you notice that “20” is the highest number that divides each of these three numbers “20”, “60”, and “100” completely, leaving no remainder
Thus, the “Highest Common Factor” or “HCF” of any given number is the unique number of “greatest value” that divides those given numbers completely.
What is the full form of “LCM”?
In the abbreviation “LCM”, the letter “L” stands for “Least”, the letter “C” stands for “Common”, and the last letter “F” stands for “Multiple”.
So, what does this “Least Common Multiple” signify?
Study the multiplication tables of “20”, “50”, and “100”.
\[\begin{matrix}
\begin{align}
20\times 1=20 \\
20\times 2=40 \\
20\times 3=60 \\
20\times 4=80 \\
20\times 5=100 \\
20\times 6=120 \\
\vdots \\
\end{align}\begin{align}
50\times 1=50 \\
50\times 2=100 \\
50\times 3=150 \\
\vdots \\
\\
\\
\\
\end{align}\begin{align}
100\times 1=100 \\
100\times 2=200 \\
\vdots \\
\\
\\
\\
\\
\end{align} \\
\end{matrix}\]
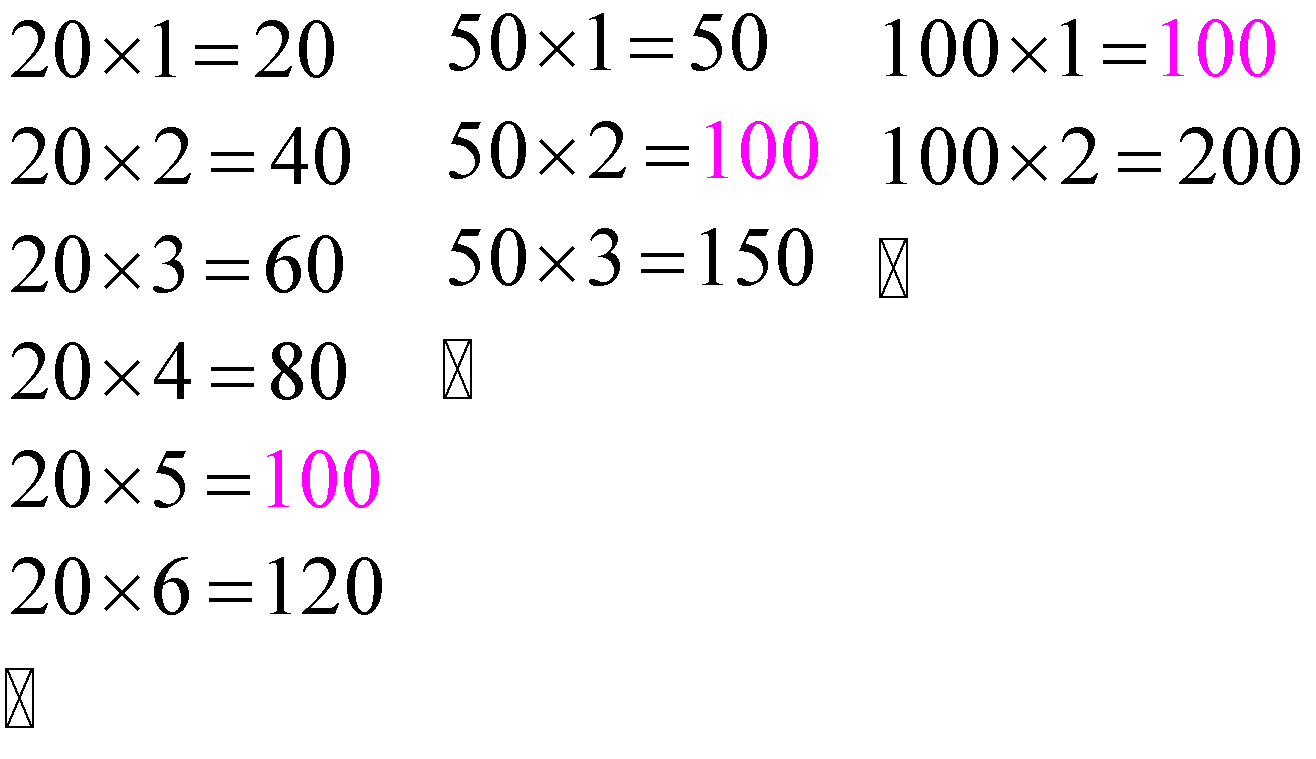
Here, you find that “100” is the first multiple which is common to “20”, “50”, and “100”. Their next “common multiples” will be having greater value than “100”.
Thus, the “Least Common Multiple” or “LCM” of “20”, “50”, and “100” is “100”. The method employed here to find “LCM” is “Listing the Multiples”.
Again, you notice that “100” is the lowest value of the number that each of these three numbers “20”, “50”, and “100” divide completely, leaving no remainder
Thus, the “Least Common Multiple” or “LCM” of any given number is the unique number of “least value” that is divided by those given numbers completely, leaving no remainder.
How do you find the “HCF” of numbers?
You can use any of the following methods to find the “HCF” of “20”, “60”, and “100”.
Factorization (discussed above)
Prime Factorization
Factorize the numbers.
\[\begin{align}
20=1\times 2\times 2\times 5 \\
60=1\times 2\times 2\times 3\times 5 \\
100=1\times 2\times 2\times 5\times 5
\end{align}\]
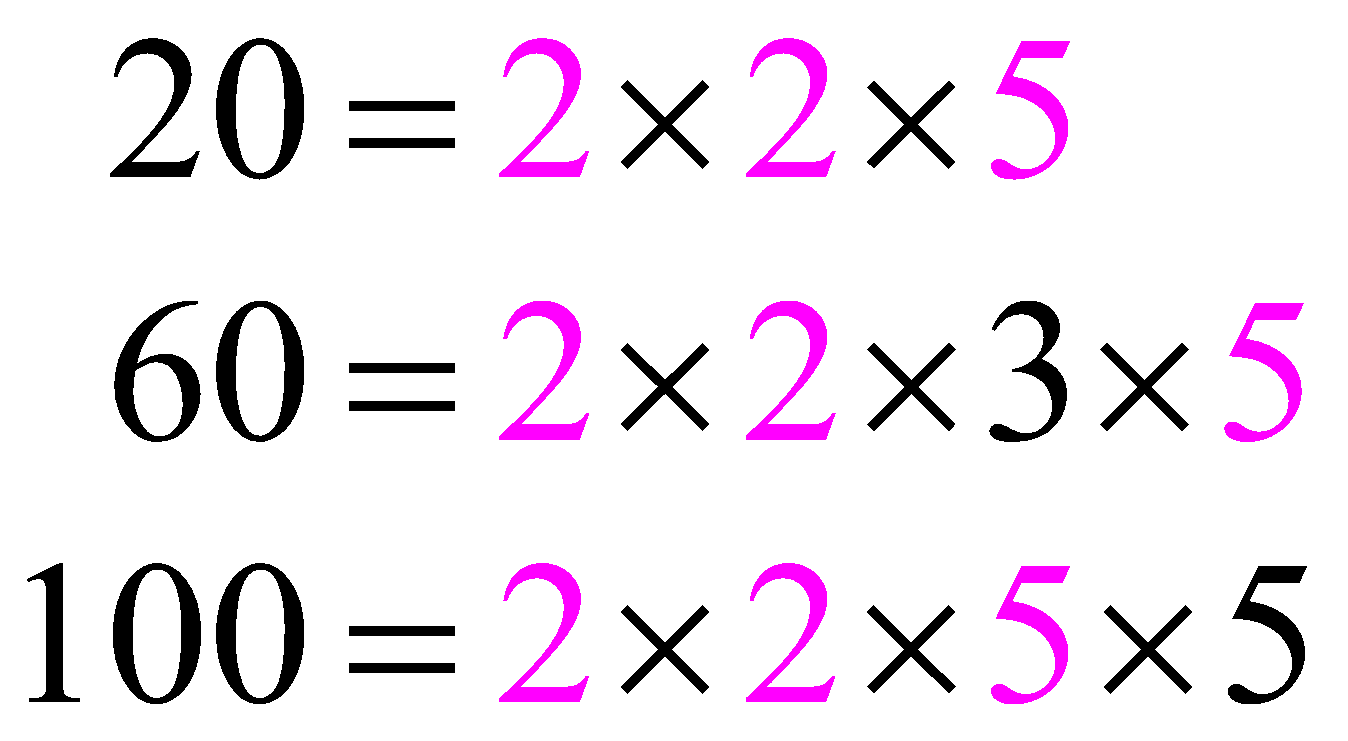
Spot the “common prime factors” of “20”, “60”, and “100” and note them.
\[1,\ 2,\ 2,\ 5\] ![]() .
.
Now, perform the following multiplication.
\[\begin{align}
\left( 1\times 2\times 2\times 5 \right) \\
=20 \\
\end{align}\]
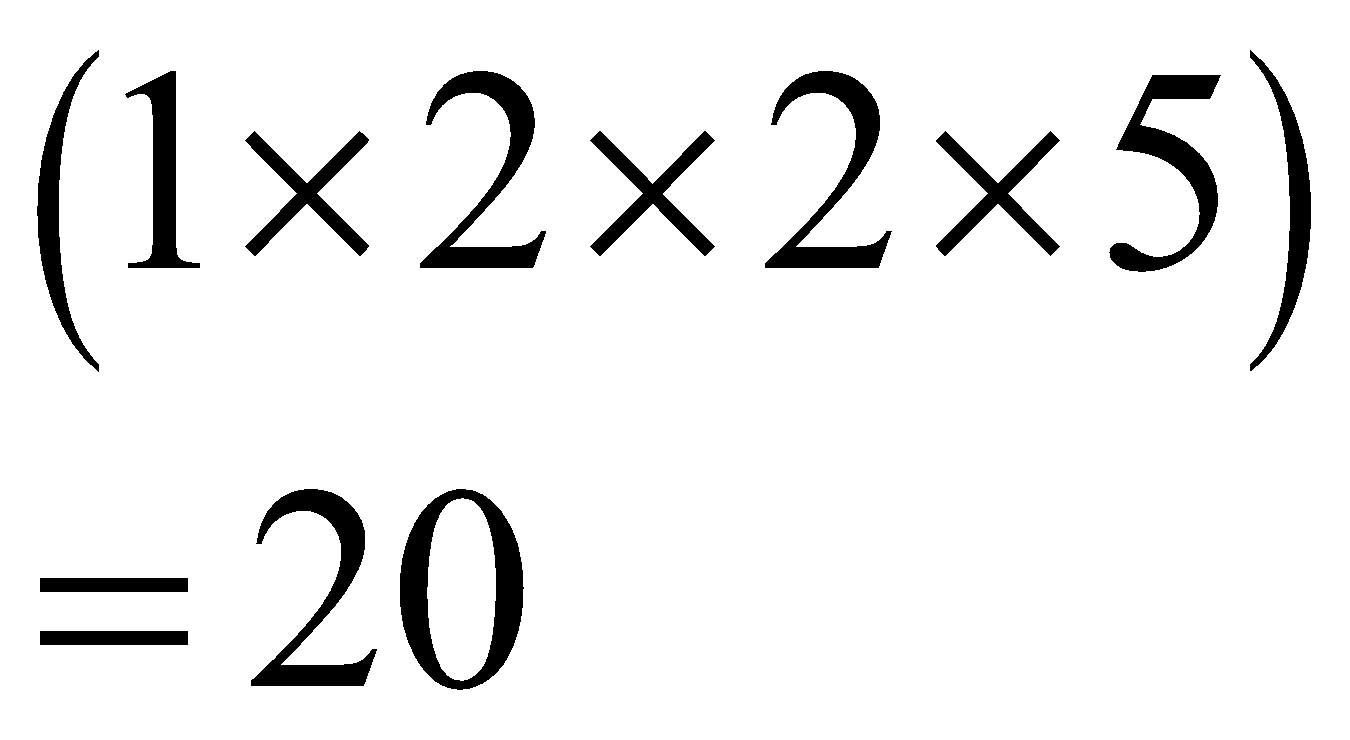
Clearly, “20” is the “HCF” of “20”, “60”, and “100”.
Division Method
Divide in the following way.
\[\begin{align}
20\underline{\overset{3}{\overline{\left){\begin{align}
60 \\
60 \\
\end{align}}\right.}}} \\
\quad \quad 0 \\
20\underline{\overset{50}{\overline{\left){\begin{align}
100 \\
10 \\
\end{align}}\right.}}} \\
\quad \quad \ 0 \\
\end{align}\]
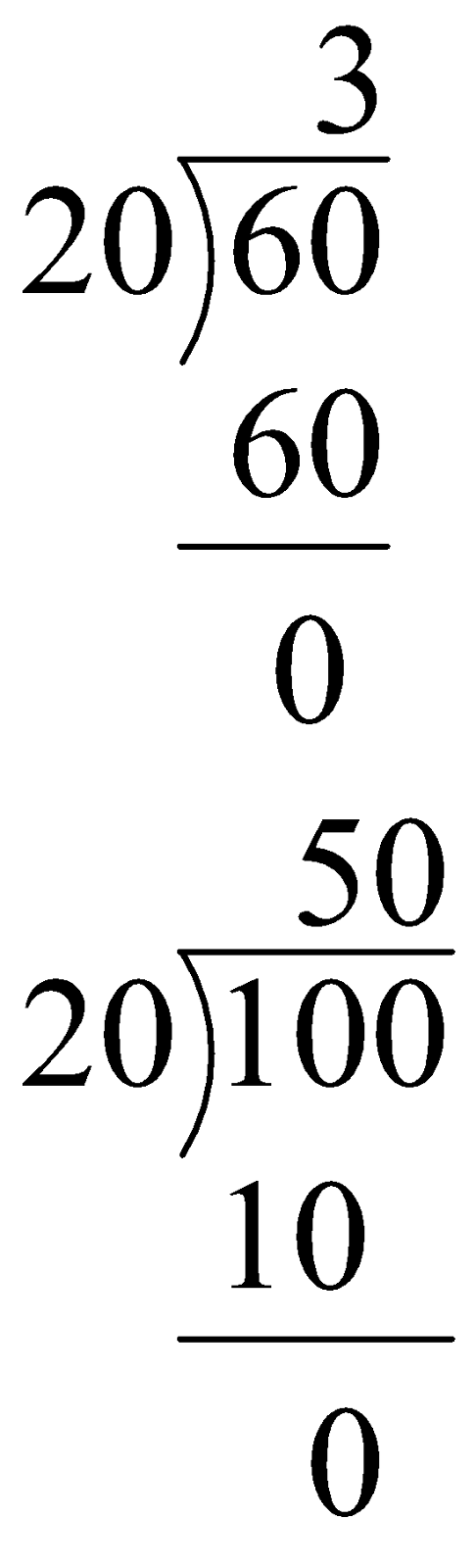
Thus, “20” is the “Highest Common Factor” of “20”, “60”, and “100”.
How do you find the “LCM” of numbers?
You can use any of the following methods to find the “LCM” of “20”, “60”, and “100”.
Listing the Multiples (discussed above)
Prime Factorization
Factorize the numbers.
\[\begin{align}
20=1\times 2\times 2\times 5 \\
60=1\times 2\times 2\times 3\times 5 \\
100=1\times 2\times 2\times 5\times 5
\end{align}\]
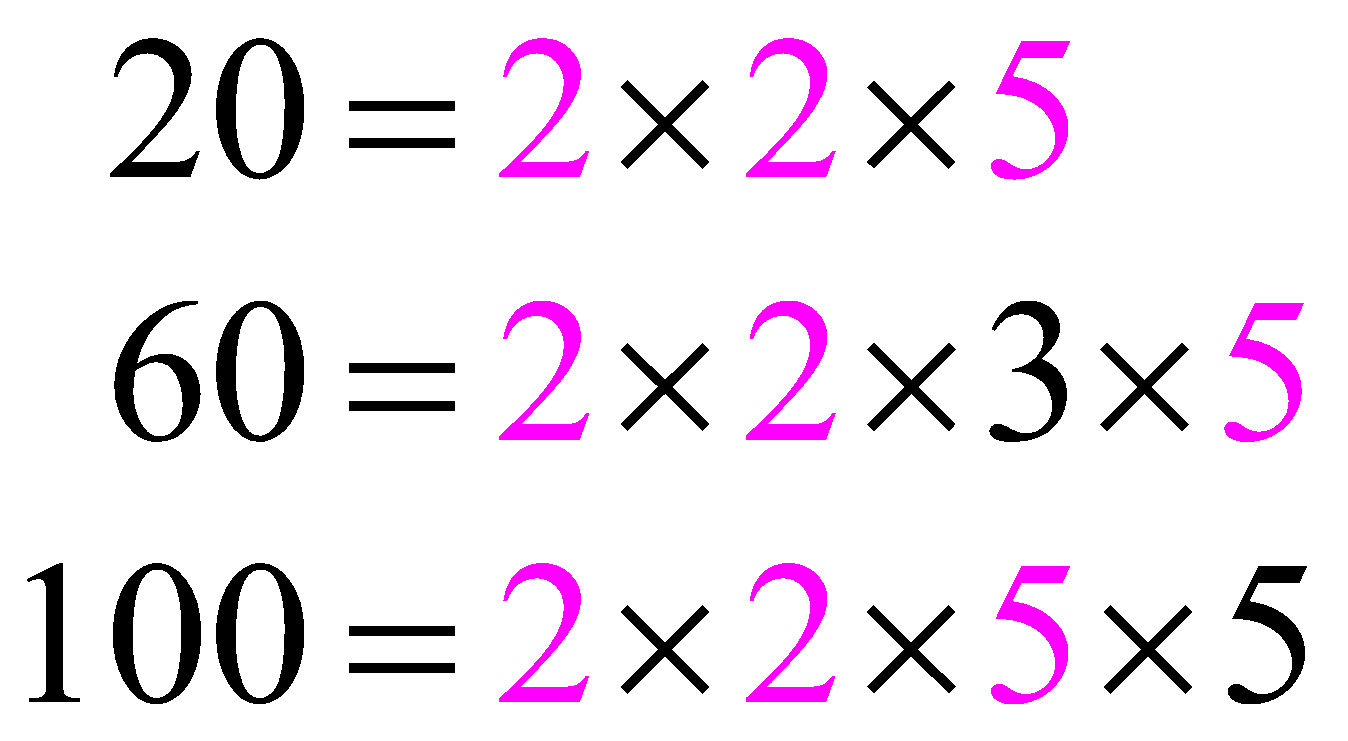
Mark the “common prime factors” of “20”, “60”, and “100” and write them.
\[1,\ 2,\ 2,\ 5\] ![]() .
.
Note the rest (uncommon) “prime factors” of “20”, “60”, and “100”.
\[3,\ 5\] ![]() .
.
Now, perform this multiplication.
\[\begin{align}
\left( 1\times 2\times 2\times 5 \right)\times \left( 3\times 5 \right) \\
=20\times 15 \\
=300 \\
\end{align}\]
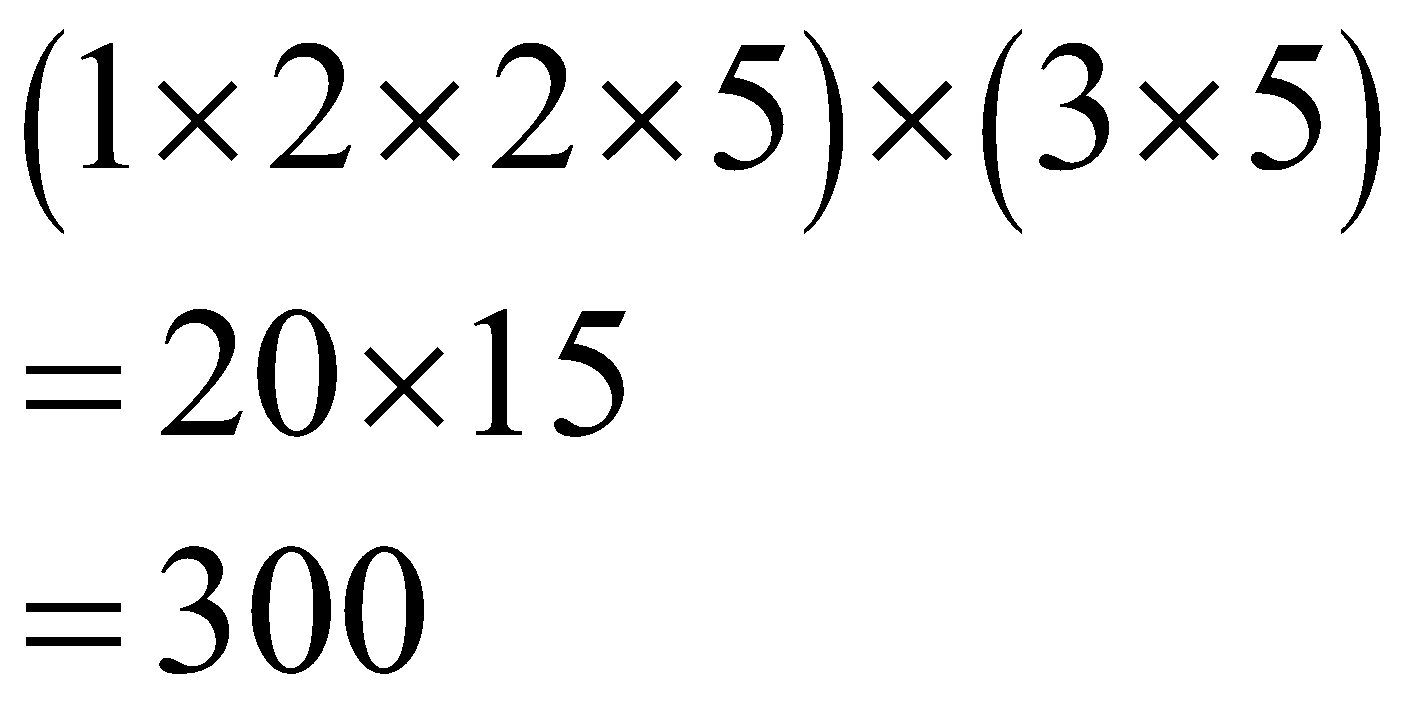
Thus, the “LCM” of “20”, “60”, and “100” is “300”.
Division Method
Group the numbers in a row, and go on dividing by prime factors which divide at least two numbers in every row.
\[2\underline{\left| 20,\ 60,\ 100 \right.}\]
![]()
Write the corresponding quotients or else copy the undivided number in the next row. Continue till you get that “no two numbers” in the row are divisible by any prime factor.
\[\begin{align}
2\ \underline{\left| 20,\ 60,\ 100 \right.} \\
2\ \underline{\left| 10,\ 30,\ 50 \right.} \\
5\ \underline{\left| \ \ 5,\ 15,\ 25 \right.} \\
\quad \ \ 1,\ \ \ 3,\ \ 5 \\
\end{align}\]
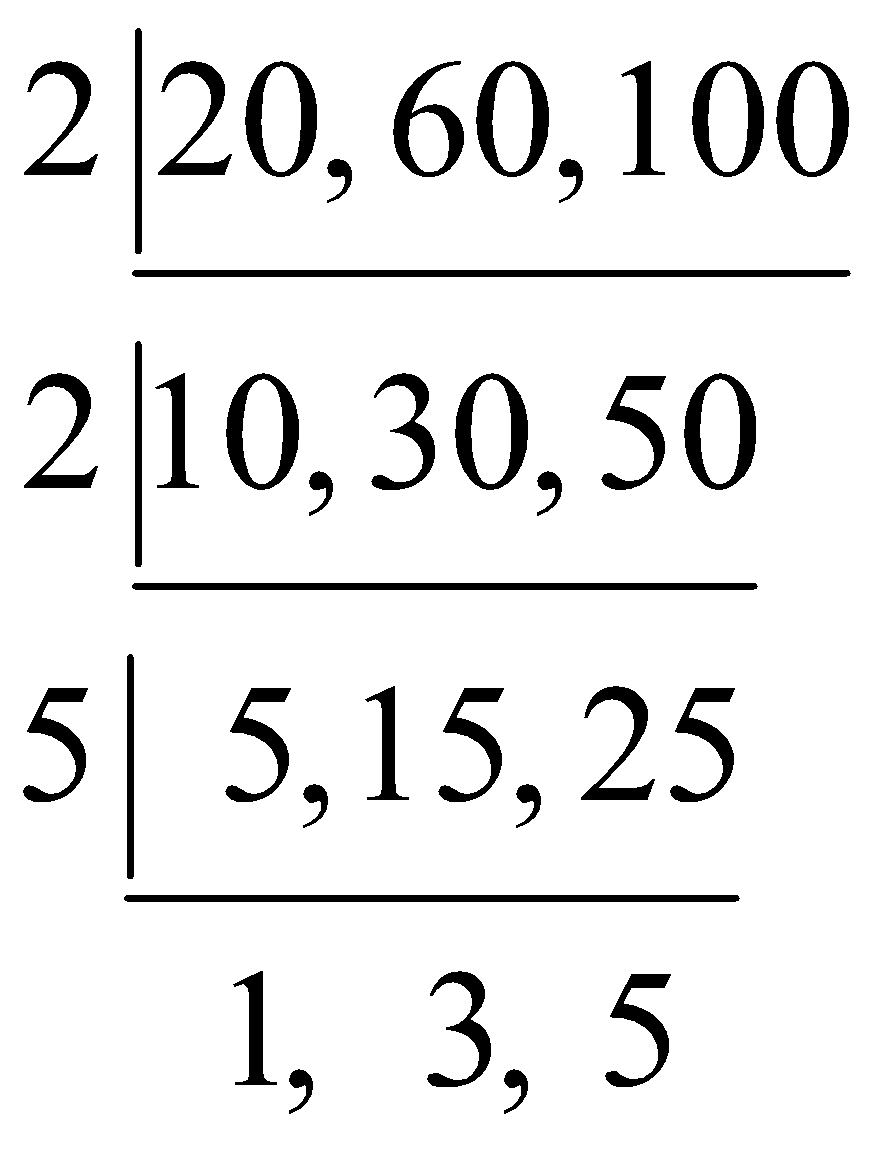
Now, perform this multiplication.
\[\begin{align}
\left( 2\times 2\times 5 \right)\times \left( 1\times 3\times 5 \right) \\
=20\times 15 \\
=300 \\
\end{align}\]
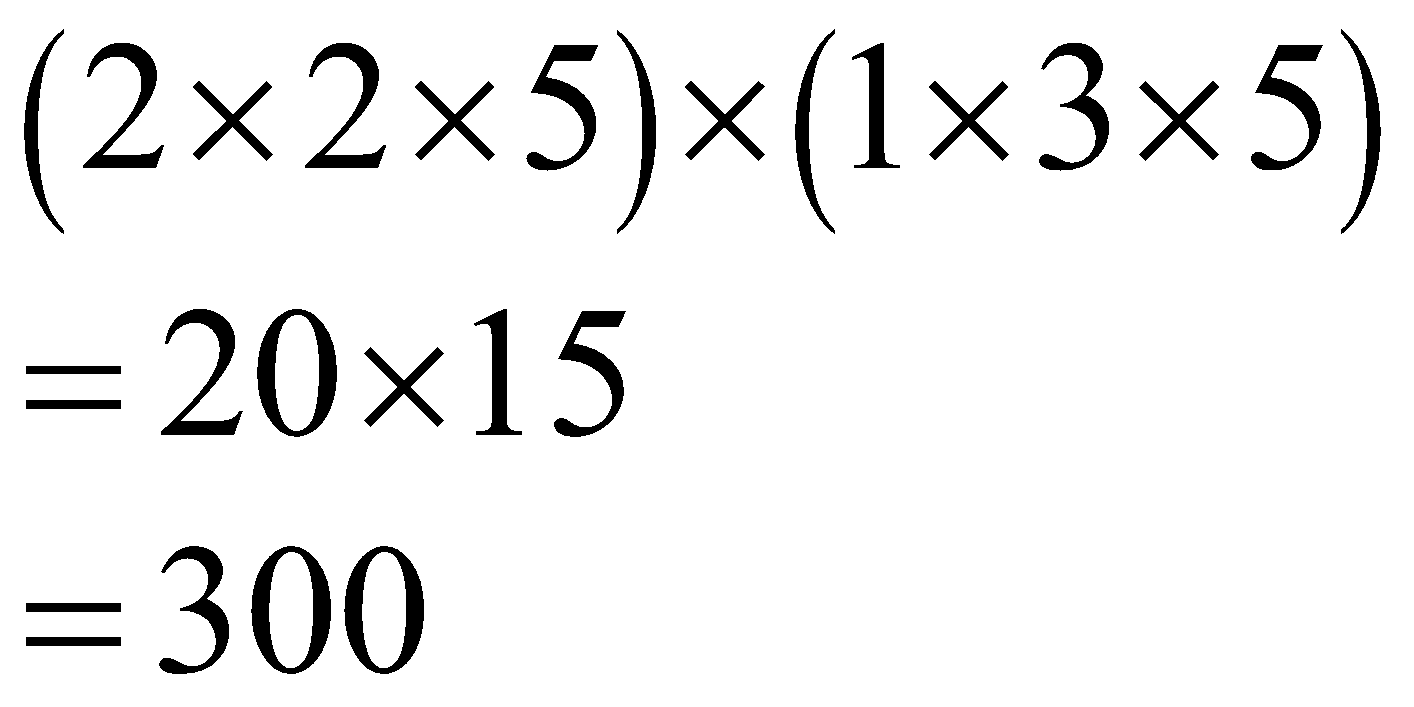
Therefore, “300” is the “Least Common Multiple” of “20”, “60”, and “100”.