IQR Full Form

What is Full Form of IQR ?

The full form of IQR is Interquartile Range. The IQR describes the middle 50% of values when ordered from lowest to highest.

The interquartile range and the median are reliable metrics, in contrast to the more well-known mean and standard deviation. Because they are independent of all values, outliers have little impact on either statistic. Additionally, the interquartile range is excellent for skewed distributions, much like the median. The percentage of observations that fall within particular ranges from the mean for normal distributions can be calculated using the standard deviation. The IQR is a great substitute, though, that doesn't work for skewed distributions because the data values fall off more abruptly on one side than the other, a skewed distribution is neither symmetric nor normal..

• The absolute measure of dispersion is defined by quartile deviation.

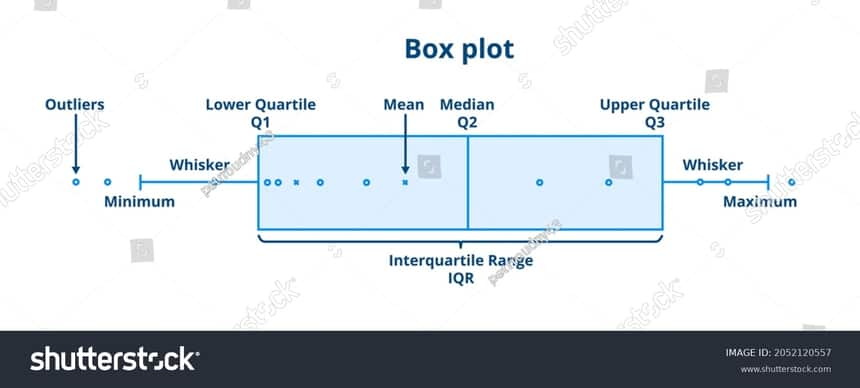
Figure 1

Formula For Interquartile Range

There are 3 quartiles. The lower quartile is represented by the letter Q1, the higher quartile by the letters Q2, and the middle quartile by the letter Q3. The higher quartile less the lower quartile equals the interquartile range, and vice versa. Below is a formula for calculating the interquartile range.

The first quartile of the series is Q1, and the third quartile is Q3, hence the interquartile range is Upper Quartile - Lower Quartile = Q3 - Q1

IQR = Q3 - Q1

Uses of IQR

• The IQR is employed to create box plots, which are straightforward graphical depictions of a probability distribution.

• Businesses utilise the IQR to indicate their income rates.

• It is possible to spot outliers using the IQR. The IQR might also show whether the dataset is skewed.