LHS And RHS Full Forms
From the first impression, it is evident that “LHS” and “RHS” are abbreviations. You will here, learn the full forms of “LHS” and “RHS”, and also their functionalities.
As such, you are acquainted with the “mathematical expressions” where you may have the “mathematical terms” on either side of the “equal to symbol” (“=”). Isn’t it right? Let us dive into it to explore further.
What Is The Full Form of “LHS”?
The full form of “LHS” indicates the “Left Hand Side”. Generally, the term “LHS” is useful in the “mathematical expressions” to denote the “mathematical terms” on the “Left Side” of the “comparators” (like “>”, “=”, etc.) in the mathematical expressions.
What Is The Full Form of “RHS”?
The full form of “RHS” indicates the “Right Hand Side”. Generally, the term “RHS” is useful in the “mathematical expressions” to denote the “mathematical terms” on the “Right Side” of the “comparators” (like “>”, “=”, etc.) in the mathematical expressions.
What Are The “Comparators”?
Look at these mathematical expressions.
\[\begin{align}
3000a+b>{{2}^{4}}\times 3\times {{5}^{3}} \\
6000\div a=3000 \\
\end{align}\]
![]()
Note that these above mathematical expressions involve some numbers [like “6000”, 3000, etc.], and certain “mathematical operators”, [like “+”, “X”, etc.].
It is definite that the “mathematical operators”, here denote corresponding “mathematical operations”.
Also, you can see the symbols “greater than” (“>”), and “equal to” (“=”) in the first and second mathematical expressions above.
Thus, these symbols which are used to compare any two “mathematical terms” or “mathematical expressions” are called “comparators”.
The following are some of the comparators with their corresponding meanings.
“=” means the “equality” of the terms on both sides.
“>” denotes the term on its “LHS” “is greater than” that on its “RHS”.
“<” suggests the term on its “LHS” “is smaller than” that on its “RHS”.
“
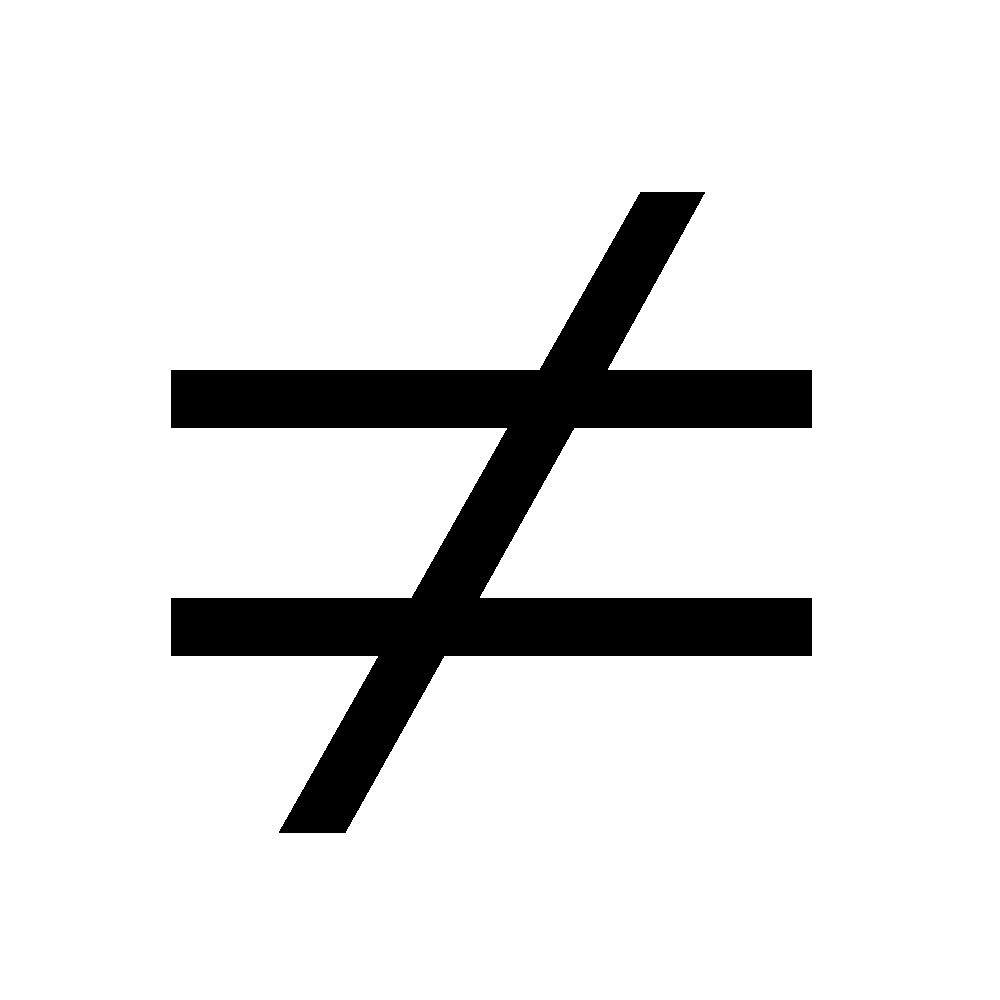 ”implies the “non-equality” of the terms on both sides.
”implies the “non-equality” of the terms on both sides.“
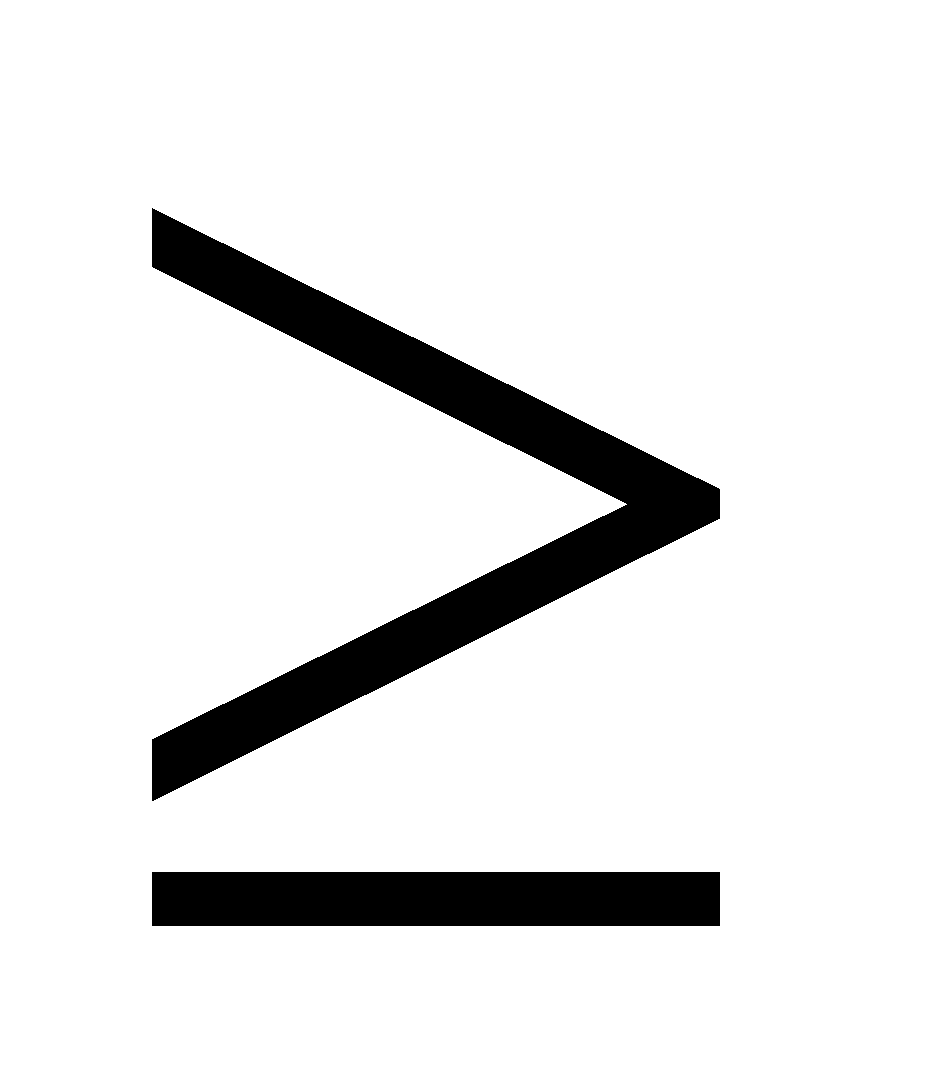 ” means the term on its “LHS” “is greater than or equal to” that on its"RHS ".
” means the term on its “LHS” “is greater than or equal to” that on its"RHS ".“
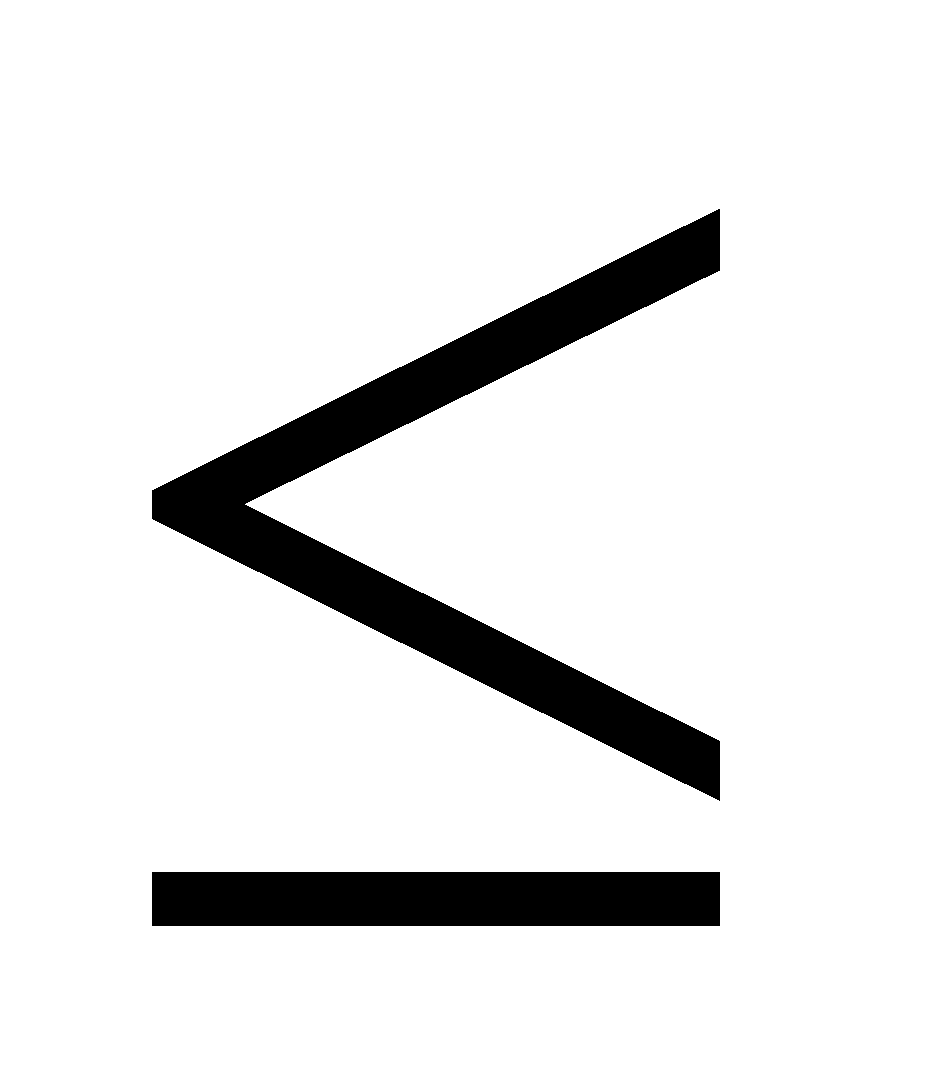 ” means the term on its “LHS " "is smaller than or equal to” that on its"RHS ".
” means the term on its “LHS " "is smaller than or equal to” that on its"RHS ".
- What Is The Full Form of “LHS”?
- What Is The Full Form of “RHS”?
- What Are The “Comparators”?
- What Are The Uses Of “LHS” And “RHS”?
What Are The Uses Of “LHS” And “RHS”?
You will find the application of the “Right Hand Side” or the “Left Hand Side” to denote the respective parts of the equations, inequalities, identities, etc.
Here are some examples which are as follows.
Prove any mathematical identity
Prove that \[{{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\]![]()
You will prove it using the terms “LHS” and “RHS” in the following way
\[\begin{align}
LHS={{\left( a+b \right)}^{2}} \\
=\left( a+b \right).\left( a+b \right) \\
=a.\left( a+b \right)+b.\left( a+b \right) \\
={{a}^{2}}+ab+ab+{{b}^{2}} \\
={{a}^{2}}+2ab+{{b}^{2}} \\
=RHS
\end{align}\]
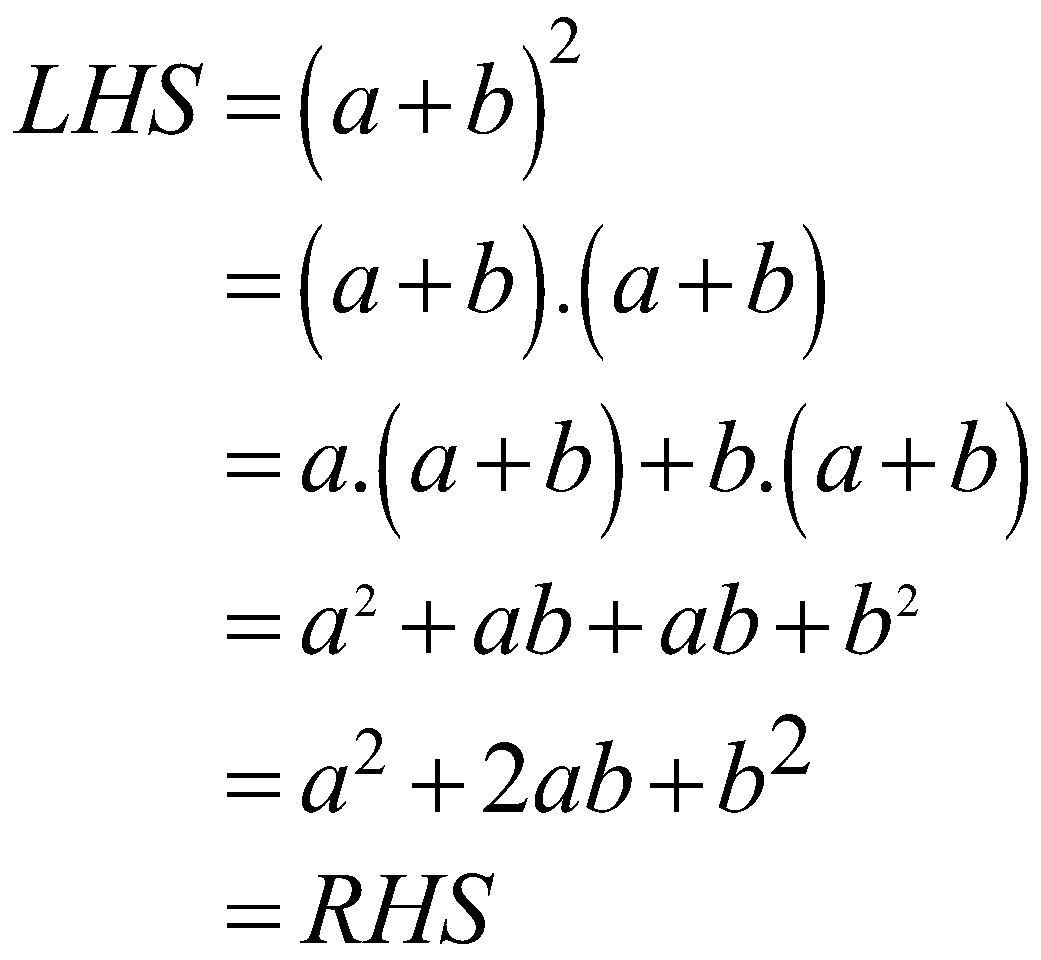
Since, the “LHS” is proved equal to the “RHS”, the mathematical identity is proved.
Prove any inequality
Prove that \[{{\left( a+b \right)}^{2}}<{{a}^{2}}+3ab+{{b}^{2}};(a,b>0)\] ![]()
You will prove it using the terms “LHS” and “RHS” in the following way
\[\begin{align}
LHS={{\left( a+b \right)}^{2}} \\
=\left( a+b \right).\left( a+b \right) \\
=a.\left( a+b \right)+b.\left( a+b \right) \\
={{a}^{2}}+ab+ab+{{b}^{2}} \\
={{a}^{2}}+2ab+{{b}^{2}} \\
RHS={{a}^{2}}+3ab+{{b}^{2}} \\
={{a}^{2}}+2ab+{{b}^{2}}+ab \\
>{{a}^{2}}+2ab+{{b}^{2}}\ (a,b>0)
\end{align}\]
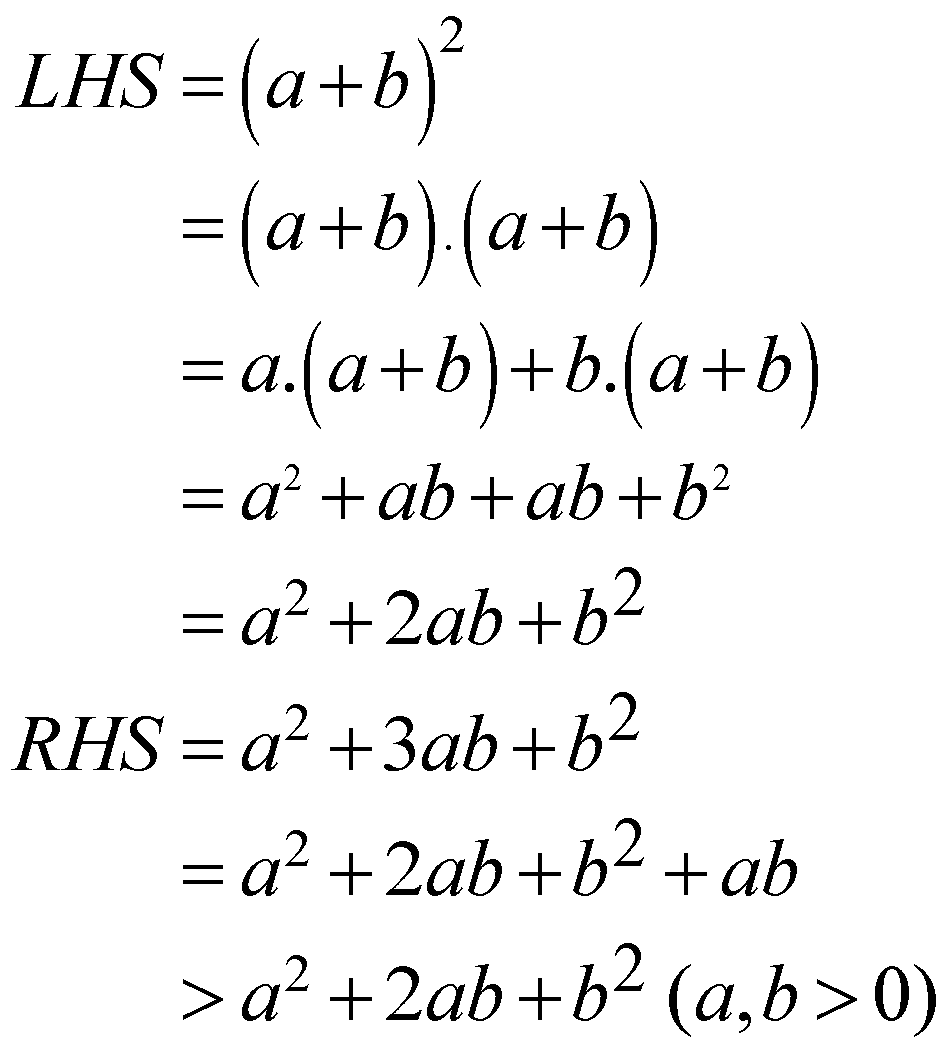
Since, the “LHS” is proved to be less than the “RHS”, the mathematical inequality is proved.
Thus, you will require the terms “RHS” and “LHS” in various cases referring to the “Right Hand Side” or the “Left Hand Side” as and when required.
Frequently Asked Questions (FAQs)
Mathematically you can deduce the following.
\[\begin{align}
LHS={{\left( a+b \right)}^{3}} \\
=\left( a+b \right).\left\{ \left( a+b \right).\left( a+b \right) \right\} \\
=\left( a+b \right).\left\{ a.\left( a+b \right)+b.\left( a+b \right) \right\} \\
=\left( a+b \right).\left\{ {{a}^{2}}+ab+ab+{{b}^{2}} \right\} \\
=\left( a+b \right).\left( {{a}^{2}}+2ab+{{b}^{2}} \right) \\
={{a}^{3}}+2{{a}^{2}}b+a{{b}^{2}}+{{a}^{2}}b+2a{{b}^{2}}+{{b}^{3}} \\
={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}} \\
=RHS
\end{align}\]
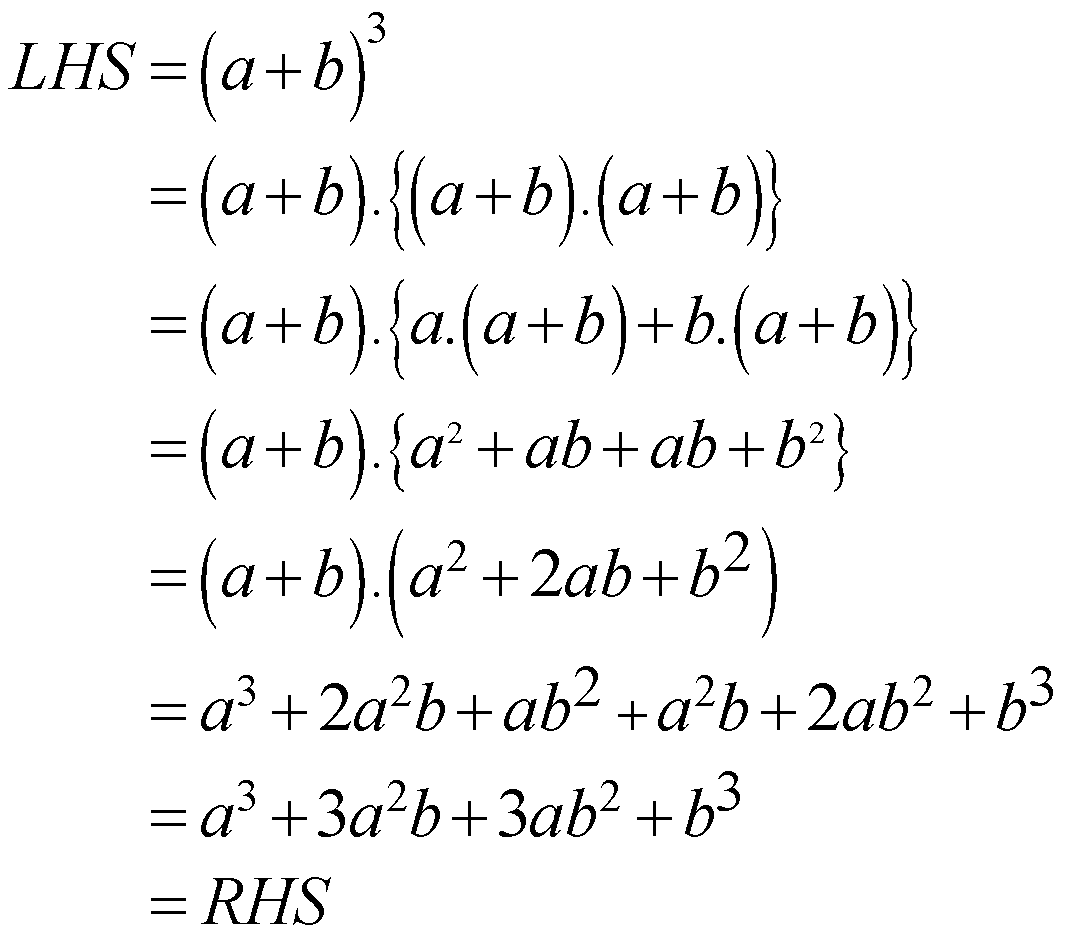
The symbol “=” means the “equality” of the terms on its both sides. Therefore, the correct option is a, “LHS” is equal to “RHS”
Mathematically you can deduce the following.
\[\begin{align}
LHS={{a}^{3}}+{{b}^{3}} \\
RHS={{\left( a+b \right)}^{3}} \\
=\left( a+b \right).\left\{ \left( a+b \right).\left( a+b \right) \right\} \\
=\left( a+b \right).\left\{ a.\left( a+b \right)+b.\left( a+b \right) \right\} \\
=\left( a+b \right).\left\{ {{a}^{2}}+ab+ab+{{b}^{2}} \right\} \\
=\left( a+b \right).\left( {{a}^{2}}+2ab+{{b}^{2}} \right) \\
={{a}^{3}}+2{{a}^{2}}b+a{{b}^{2}}+{{a}^{2}}b+2a{{b}^{2}}+{{b}^{3}} \\
={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}} \\
>{{a}^{3}}+{{b}^{3}} \\
So,LHS<\ RHS
\end{align}\]
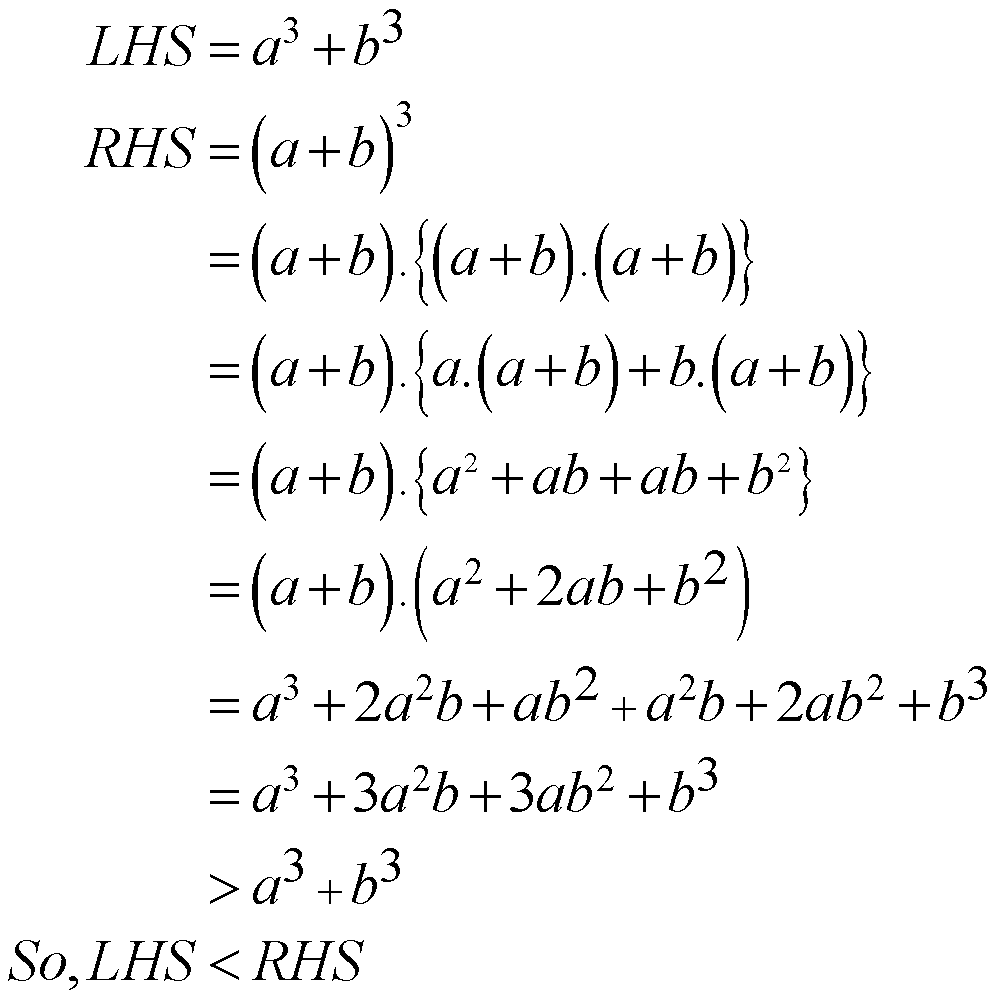
The symbol “<”suggests the term on its “LHS” “is smaller than” that on its “RHS”.. Therefore, the correct option is d, “LHS” is less than “RHS”
Mathematically you can deduce the following.
\[\begin{align}
LHS={{\left( a+b \right)}^{2}} \\
=\left( a+b \right).\left( a+b \right) \\
=a.\left( a+b \right)+b.\left( a+b \right) \\
={{a}^{2}}+ab+ab+{{b}^{2}} \\
={{a}^{2}}+2ab+{{b}^{2}} \\
RHS={{a}^{2}}-{{b}^{2}}<{{a}^{2}}+2ab+{{b}^{2}} \\
So,LHS>\ RHS
\end{align}\]

The symbol “>”denotes the term on its “LHS” “is greater than” that on its “RHS”. Therefore, the correct option is c, “LHS” is greater than “RHS”.
The symbol “![]() ”implies the “non-equality” of the terms on both sides. Therefore, the correct option is b, “LHS” is not equal to “RHS”.
”implies the “non-equality” of the terms on both sides. Therefore, the correct option is b, “LHS” is not equal to “RHS”.