LPP Full Form
Introduction
LPP is an abbreviation that stands for linear programming problem. It is a problem of optimizing a linear function in operational research. We can also define LPP as a technique for effective and efficient utilization of limited resources to achieve organizational goals. This tool is used in many research industries, investment portfolios, etc. to make right decisions. It is also used in computer science, mathematics, economics, and many other fields. Linear programming is used to find the most optimal solution to a problem with specific constraints.
What Is A Linear Programming Problem?
The Linear Programming Problem is the method aimed at the formation of a linear equation and its optimization using the relevant constraints such that the minimization or maximization of the desired attributes can be obtained through mathematical modeling.
What Are The Components In A Linear Programming Problem?
Basically, these are the following components that shape up a linear programming problem.
Objective Function
The linear equation that represents the mathematical model of the actual scenario. It either maximizes or minimizes to give the optimal solution of an LPP
Decision Variables
The variables that are incorporated to design the objective function. Generally, two variables are considered and both are non-negative and linear. However, more than two variables may be present in complex real-life problems.
Constraints
The limiting factors of the mathematical model of the actual scenario are represented as the requisite number of inequalities or equalities or their any combination. They are referred to as constraints.
Non-Negative Restrictions
In case some or all decision variables may take negative values, there are assigned some non-negative restrictions in terms of inequalities.
What Is The Methodology Of A Linear Programming Problem?
The methodology of a linear programming problem is described under the following points:
Understanding the real-life problem.
Defining the decision variables
Describing the objective clearly.
Framing the objective function
Conceptualizing the aim of maximization or minimization of the optimal solution
Defining the constraints
Go for the process of obtaining the optimal solution.
The Types of Solutions of A Linear Programming Problem
The following are the types of solutions that a linear programming problem can have depending upon the constraints of a particular linear programming problem.
Finite number of Optimal Solutions
Infinite number of Optimal Solutions
Single Optimal Solution
No Optimal Solution
What Are The Methods of Finding Solutions of A Linear Programming Problem?
The noteworthy methods of finding solutions of a linear programming problem are the following.
Graphical Method
Simplex Method
The Graphical Method of Solution Of A Linear Programming Problem
The graphical method of solving a linear programming problem (LPP) is described under the following points:
Write the linear programming problem involving the objective function, constraints, and restrictions.
First create the graphs of all the inequalities defining the constraints one by one.
For every constraint inequality, plot a line by joining its vertical and horizontal intercepts obtained by equating each constraint equation.
Find the valid side of each constraint line pertaining to the corresponding constraint equation.
Mark the intersections of all the different constraint lines to determine the common area called the feasible solution region.
Feasible region in an LPP denotes the set of points which satisfy all of the given constraints.
Points within and on the boundary of the feasible region represent feasible solutions of the constraints.
A corner point is a point of intersection of two boundary lines in the feasible region.
If the feasible region of the given LPP is defined to be bounded, the maximum and minimum values of the objective function occur at the corner points.
The maximum or minimum value of an objective function is known as the optimal value of LPP. These values are obtained at corner points.
If the value of the objective function of an LPP remains the same at two corners, it is the same at every point on the line joining two corner points.
Thus when an LPP attains its maximum value at two corner points of the feasible region, it will attain maximum value at infinitely many points.
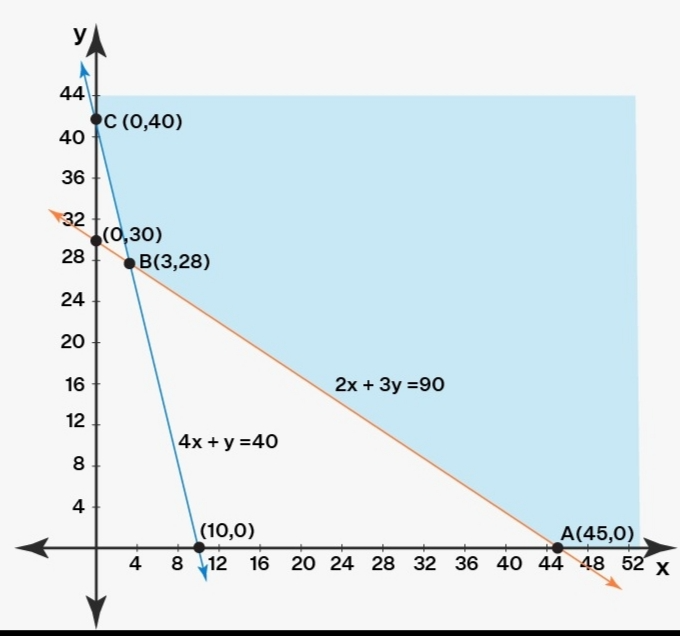
Example
Solve the given linear programming problem using the graphical method.
Minimize, Z = 5x+ 4y \[Z=5x+4y}\
4x+y 40 \[4x+y \geq 40]\
2x+3y 90 \[2x+3y \geq 90]\
x, y 0 \[(x, y) \geq 0]\
Solution: Equation of lines are
4x+y= 40 \[4x+y= 40]\ and 2x+3y = 90 \[2x+3y=90]\.
(0, 40) and (10,0) are points passed through the first equation (4x+y = 40) \[4x+y= 40]\ . So all the points which are lying on or above this line satisfy this equation.
Whereas (0,30) and (45,0) are the points passing through (2x+3y = 90) \[2x+3y=90]\. So, all the points lying on or above this line satisfy this equation
Corner points | Z = 5x+4y \[Z=5x+4y}\ |
A = (45,0) | 225 |
B = (3,28) | 127 |
C = (0,40) | 160 |
Now, when we observe the feasible region, it is an unbounded region here.
Hence, we check for the line 5x+4y = 127. we would observe that this line intersects the feasible region at only one point which is (3,28).
Hence, Minimum value of Z is 12 and hence point(3,28) gives the optimal solution.
Applications Of Linear Programming
The importance of linear programming in different fields is explained below:
Energy industry: linear programming in the energy industry provides different methods to optimize the electric power system
Transportation optimization: Here linear programming is used for cost and time efficiency
Efficient manufacturing: one of the important applications of linear programming is to make maximum profit
Engineering: Some designs and manufacturing problems can be easily solved by using linear programming.
Some Myths about LPP
The following are some of the myths about LPP which are not true at all.
It is necessary to find the objective function value at every point in the feasible region to find the optimum value of the objective function.
The optimal value of the objective function is attained at the points on X-axis only.
Frequently Asked Questions (FAQs)
The Simplex Method of Linear Programming Problems involves the solution through iterations to improve the optimal value of the objective function, where there can be more than two decision variables.
A Slack variable is a type of additional variable in the Simplex method of Linear Programming Problems. It refers to indicate the quantity of unused resources.
A Surplus variable is a type of additional variable in the Simplex method of Linear Programming Problems. It refers to indicate the quantity of unused resources by which the left-hand side of the referred equation exceeds the minimum limit.
An Artificial variable is a type of additional variable in the Simplex method of Linear Programming Problems. As its name suggests, it refers to indicate the temporary slack variables which are used during the process of calculations and are removed thereafter.
The additional variables are introduced in the Simplex method of Linear Programming Problem to convert the inequalities defining the constraints into equations for solving the LPP.