A Cube Plus B Cube Formula

Q: What is the formula of a cube plus b cube plus c cube?

A cube plus B cube plus C cube formula is given by, $a^3+b^3+c^3=(a+b+c)(a^2+b^ 2+c^2-ab-bc-ca)+$ 3abc.

Q: What is a cube minus b cube?

A cube minus B cube is equal to $(a-b) (a^2 + ab + b^2)$.

Q: What is identity of a cube plus b cube?

A cube plus b cube equals to $(a + b) (a^2 - ab + b^2)$.

Q: Write the factors of a cube plus b cube.

A cube plus B cube equals to $(a+b)(a^2-ab+b^2)$.

A Cube Plus B Cube Formula | a^3 + b^3 Formula

Edited By Team Careers360 | Updated on Jul 02, 2025 05:32 PM IST

Algebra is one of the fundamental concept in mathematics. Algebra is of the main concpets which helps in solving complex algebraic equations within no time. In this article, we will discuss about another such useful identity that makes the process of calculating cubes of numbers very easy. We will learn about what is a cube plus b cube formula along with various examples for better understanding.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

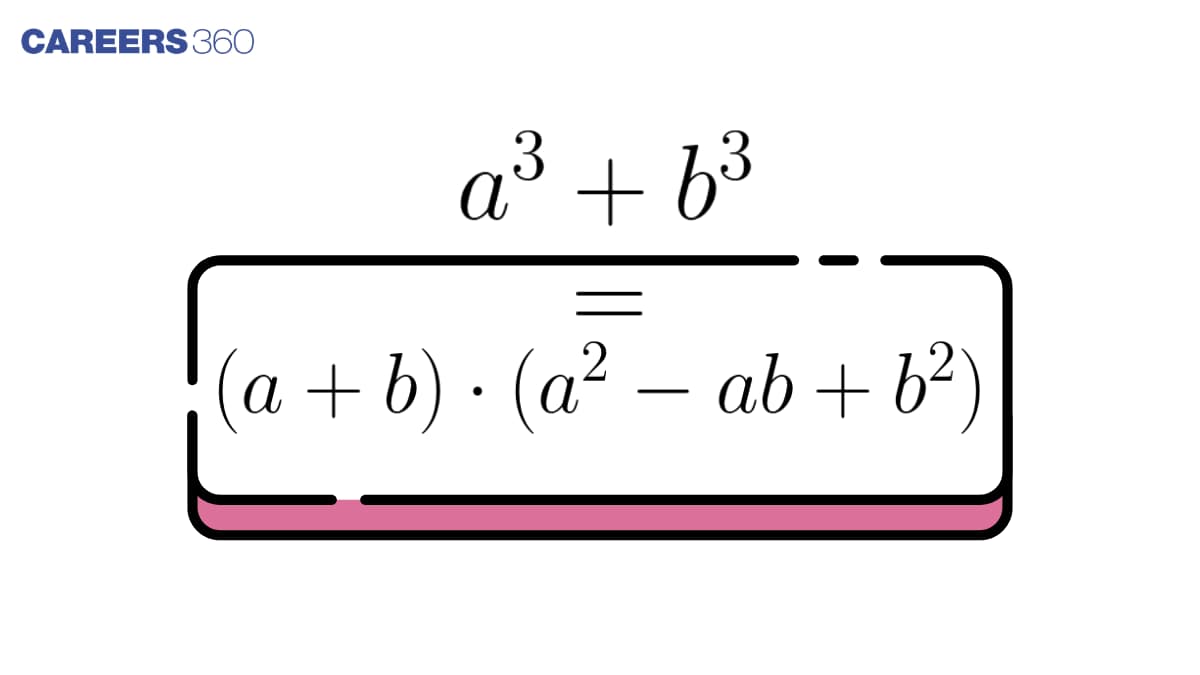
A Cube Plus B Cube Formula | a^3 + b^3 Formula

The $a^{3} + b^{3}$ formula is also known as the sum of cubes (of two numbers) formula, widely used to find the sum of cubes of 2 numbers when we do not know their real values. It has various applications in factorization also.

Formula of a cube plus b cube is expressed as : a cube plus b cube is equals to :

$a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2})$

Identity of a Cube plus b Cube

Now, let us verify a cube plus b cube formula.

$LHS = a^{3} + b^{3}$

When we simplify RHS side we get,

$= (a + b) (a^{2} - a b + b^{2})$

Now we multiply $a$ and $b$ separately with $(a^{2} - a b + b^{2})$ we get

$\begin{aligned} = a (a^{2} - a b + b^{2}) + b (a^{2} - a b + b^{2}) \\ = a^{3} - a^{2} b + a b^{2} + a^{2} b - a b^{2} + b^{3} \\ = a^{3} - a^{2} b + a^{2} b + a b^{2} - a b^{2} + b^{3} \\ = a^{3} - 0 + 0 + b^{3} \\ = a^{3} + b^{3} \end{aligned}$

^{Examples on a cube plus b cube formula}

Example 1: Find the value of $105^{3} + 7^{3}$ by using the formula of a cube plus b cube.

Solution: To find: $105^{3} + 7^{3}$ .

We assume that $a = 105$ and $b = 7$ .

Substituing values, a cube plus b cube is equal to :

$\begin{aligned} a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2}) \\ 105^{3} + 7^{3} = (105 + 7) (105^{2} - (105) (7) + 7^{2}) \\ = (112) (11025 - 735 + 49) \\ = (112) (10339) \\ = 1157968 \end{aligned}$

Example 2: Factorize the expression $125 x^{3} + 27$ by using a cube plus b cube identity.

Solution: To factorize: $125 x^{3} + 27$ .

We will use the formula for a cube plus b cube to factorize this.

We write the given expression as a cube plus b cube equals to :

$125 x^{3} + 27 = (5 x)^{3} + 3^{3}$

We will substitute $a = 5 x$ and $b = 3$ in the formula of a cube plus b cube.

$\begin{aligned} a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2}) \\ (5 x)^{3} + 3^{3} = (5 x + 3) ((5 x)^{2} - (5 x) (3) + 3^{2}) \\ = (5 x + 3) (5 x^{2} - 15 x + 9) \end{aligned}$

Example 3 : Simplify $29^{3} + 30^{3}$ using a cube plus b cube formula.

Solution: To find $29^{3} + 30^{3}$

Let us assume $a = 29$ and $b = 30$

A cube plus B cube is equal to : $a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2})$

We substitute these in the a cube plus b cube identity.

$\begin{aligned} a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2}) \\ 29^{3} + 30^{3} = (29 + 30) (29^{2} - (29) (30) + 30^{2}) \\ = (59) (841 - 870 + 900) \\ = (59) (871) \\ = 51389 \end{aligned}$

Example 4: Factor $y^{3}$ + 125.

Solution: $y^{3} + 125$ can be written as $y^{3} + 5^{3}$

Now, $y^{3} + 5^{3}$ is in the form of $a^{3} + b^{3}$ .

Using the a cube plus b cube identity, $a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2})$ , we get,

$\begin{aligned} y^{3} + 5^{3} = (y + 5) (y^{2} - 5 y + 5^{2}) \\ y^{3} + 5^{3} = (y + 5) (y^{2} - 5 y + 25) \end{aligned}$

Example 5: Factor the expression $27 x^{3} + 8$ .

Solution: $27 x^{3} + 8$ can be written as $(3 x)^{3} + 2^{3}$

On comparing with formula of a cube plus b cube, we get $a^{3} + b^{3} = (a + b) (a^{2} - ab + b^{2})$ , we have; $a = 3 x$ and $b = 2$

Therefore, $(3 x)^{3} + 2^{3} = (3 x + 2) [(3 x)^{2} - (3 x) \cdot (2) + 2^{2}]$ (using a cube plus b cube formula)

$27 x^{3} + 8 = (3 x + 2) [9 x^{2} - 6 x + 4]$

List of Topics Related to A cube plus B cube Formula

Algebra	Algebraic Identities Class 8
Algebraic Expressions	Algebraic Identities Class 9
Algebra Class 6

Frequently Asked Questions (FAQs)

1. What is the formula of a cube plus b cube?

A cube plus B cube formula, or the factors of a cube plus b cube, $a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2})$ .

2. What is the formula of a cube plus b cube plus c cube?

A cube plus B cube plus C cube formula is given by, $a^{3} + b^{3} + c^{3} = (a + b + c) (a^{2} + b^{2} + c^{2} - a b - b c - c a) +$ 3abc.

3. What is a cube minus b cube?

A cube minus B cube is equal to $(a - b) (a^{2} + a b + b^{2})$ .

4. What is identity of a cube plus b cube?

A cube plus b cube equals to $(a + b) (a^{2} - a b + b^{2})$ .

5. Write the factors of a cube plus b cube.

A cube plus B cube equals to $(a + b) (a^{2} - a b + b^{2})$ .

6. Can the a³ + b³ formula be applied to variables other than a and b?

Yes, the formula can be applied to any variables or expressions. For example, x³ + y³, (2x)³ + (3y)³, or even (x + 1)³ + (x - 2)³ can all be factored using this formula.

7. Can you use the a³ + b³ formula to factor expressions like 8x³ + 27y³?

Yes, you can factor 8x³ + 27y³ using this formula. First, factor out the coefficients: 8x³ + 27y³ = (2x)³ + (3y)³. Then apply the formula: (2x + 3y)((2x)² - (2x)(3y) + (3y)²) = (2x + 3y)(4x² - 6xy + 9y²).

8. How is the a³ + b³ formula related to cubic equations?

The a³ + b³ formula is useful in solving certain types of cubic equations. If a cubic equation can be rearranged into the form x³ + y³ = k, this formula can help in finding solutions.

9. Why is it important to recognize the pattern of a³ + b³ in algebraic expressions?

Recognizing this pattern allows for quick factorization of certain expressions, simplifying calculations and equation solving. It's a key pattern in algebra that often appears in more complex problems.

10. How does the a³ + b³ formula relate to the concept of perfect cubes?

The a³ + b³ formula shows that the sum of two perfect cubes is not itself a perfect cube. Instead, it's the product of a linear term and a quadratic term.

11. What is the formula for a³ + b³?

The formula for a³ + b³ is a³ + b³ = (a + b)(a² - ab + b²). This formula expands the sum of two cubes into a product of two factors.

12. Why is the a³ + b³ formula useful in algebra?

The a³ + b³ formula is useful because it allows us to factor the sum of two cubes, simplifying complex expressions and solving equations involving cubic terms.

13. Can you explain the geometric interpretation of the a³ + b³ formula?

Geometrically, a³ + b³ represents the sum of the volumes of two cubes with sides a and b. The formula shows how this sum can be represented as the product of the sum of their sides (a + b) and a quadratic expression (a² - ab + b²).

14. Why is there a negative term (-ab) in the second factor of the a³ + b³ formula?

The negative term (-ab) in the second factor is necessary to balance the expansion. When you multiply (a + b)(a² - ab + b²), the -ab term ensures that the middle terms cancel out, leaving only a³ and b³.

15. Why doesn't the a³ + b³ formula factor completely into linear terms?

The a³ + b³ formula doesn't factor completely into linear terms because the second factor (a² - ab + b²) is irreducible over real numbers. It can only be factored further if complex numbers are allowed.

16. How does the a³ + b³ formula differ from the a³ - b³ formula?

The a³ + b³ formula is (a + b)(a² - ab + b²), while the a³ - b³ formula is (a - b)(a² + ab + b²). The main difference is in the signs of the terms and the middle term of the second factor.

17. How does the a³ + b³ formula compare to other polynomial identities?

The a³ + b³ formula is one of several important polynomial identities, along with others like (a + b)², (a - b)², and a² - b². Each serves a specific purpose in algebraic manipulation and problem-solving.

18. What is the relationship between the a³ + b³ formula and the difference of cubes formula?

The a³ + b³ formula and the difference of cubes formula (a³ - b³) are complementary. They both factor cubic expressions, but one deals with the sum of cubes while the other deals with the difference of cubes.

19. Can the a³ + b³ formula be used in calculus?

Yes, the formula can be useful in calculus, particularly in integration. Recognizing a³ + b³ patterns can help in simplifying integrals or finding antiderivatives of certain expressions.

20. What common mistakes do students make when using the a³ + b³ formula?

Common mistakes include confusing it with the difference of cubes formula, forgetting the negative sign in the middle term of the second factor, or misapplying it to expressions that aren't actually sums of cubes.

21. How does understanding the a³ + b³ formula help in factoring more complex expressions?

Understanding this formula helps in recognizing and factoring more complex expressions that contain the sum of two cubes as a part of them. It's a building block for tackling more advanced polynomial factorizations.

22. How does the a³ + b³ formula extend to higher powers?

The a³ + b³ formula is specific to cubes and doesn't directly extend to higher powers. For higher powers, different formulas and techniques are used, such as the sum and difference of nth powers formulas.

23. How does the a³ + b³ formula relate to the concept of conjugates in algebra?

While not directly related to conjugates, the a³ + b³ formula shares a similarity with the concept. Just as (a + b)(a - b) factors a² - b², (a + b)(a² - ab + b²) factors a³ + b³.

24. Can the a³ + b³ formula be applied to expressions with fractional or irrational exponents?

The formula specifically applies to cubes (exponent 3). For fractional or irrational exponents, different techniques would be needed, although similar principles might apply in some cases.

25. What's the connection between the a³ + b³ formula and the rational root theorem?

While not directly connected, both the a³ + b³ formula and the rational root theorem are tools for dealing with cubic expressions. The formula helps in factoring, while the theorem helps in finding potential roots.

26. Why doesn't factoring a³ + b³ result in (a + b)(a + b)(a + b)?

(a + b)(a + b)(a + b) expands to a³ + 3a²b + 3ab² + b³, which includes additional terms not present in a³ + b³. The a³ + b³ formula specifically factors out only the sum of two cubes.

27. Can the a³ + b³ formula be applied in three-dimensional geometry?

Yes, the formula has applications in 3D geometry, particularly when dealing with volumes of cubes or cubic shapes. It can help in calculations involving the sum of volumes of two cubic objects.

28. How does understanding the a³ + b³ formula contribute to algebraic thinking?

Understanding this formula enhances algebraic thinking by demonstrating how complex expressions can be factored and simplified. It encourages students to look for patterns and relationships in algebraic expressions.

29. How does the a³ + b³ formula relate to the concept of algebraic identities?

The a³ + b³ formula is an important algebraic identity. Like other identities, it expresses an equality that holds true for all values of the variables involved, making it a powerful tool in algebraic manipulation.

30. What's the connection between the a³ + b³ formula and the concept of factoring by grouping?

While the a³ + b³ formula is not directly related to factoring by grouping, both are techniques for factoring polynomials. The formula provides a direct method for a specific type of expression, while factoring by grouping is a more general approach.

31. How does the a³ + b³ formula relate to the binomial expansion of (a + b)³?

The a³ + b³ formula is not directly related to the binomial expansion of (a + b)³. The binomial expansion includes additional terms (3a²b and 3ab²) that are not present in a³ + b³.

32. How can understanding the a³ + b³ formula improve mental math skills?

While not commonly used for mental math, understanding this formula can improve algebraic intuition and pattern recognition, which are valuable skills in mental math and estimation.

33. What role does the a³ + b³ formula play in the study of polynomial functions?

This formula is crucial in understanding the behavior of cubic functions, particularly in factoring and finding roots. It's a key tool in the broader study of polynomial functions and their properties.

34. Can the a³ + b³ formula be used in reverse to expand expressions?

Yes, if you encounter an expression in the form (a + b)(a² - ab + b²), you can use the formula in reverse to expand it to a³ + b³.

35. How does understanding the a³ + b³ formula contribute to problem-solving skills in algebra?

Understanding this formula enhances problem-solving skills by providing a tool for simplification and factorization. It also improves pattern recognition and algebraic manipulation abilities.

36. How can you verify that the a³ + b³ formula is correct?

You can verify the formula by expanding (a + b)(a² - ab + b²):

37. How does the a³ + b³ formula relate to the concept of algebraic proofs?

The formula can be used in algebraic proofs, especially those involving cubic expressions. Understanding and applying this formula in proofs helps develop skills in logical reasoning and mathematical argumentation.

38. How can visualizing the a³ + b³ formula geometrically aid in understanding?

Geometrically, a³ + b³ can be visualized as the sum of two cube volumes. The factorization can be understood as dividing this total volume into a more complex shape represented by (a + b)(a² - ab + b²), which can help in grasping the abstract algebraic concept.

39. How does the a³ + b³ formula relate to the study of polynomial roots?

This formula is valuable in the study of polynomial roots as it provides a factorization for certain cubic polynomials. Understanding this can help in identifying potential roots and in analyzing the behavior of cubic functions.

40. What's the significance of the term a² - ab + b² in the a³ + b³ formula?

The term a² - ab + b² is significant because it's a quadratic expression that, when multiplied by (a + b), produces a³ + b³. It's also interesting because it's always positive for real, non-zero a and b.

41. How can you remember the a³ + b³ formula?

A helpful mnemonic is "SOH" - Sum, Opposite, Hybrid. The first term is the Sum (a + b), the second factor starts with a², then the Opposite (-ab), and ends with b² (Hybrid of a and b).

42. How does the a³ + b³ formula relate to polynomial long division?

The a³ + b³ formula provides a shortcut for what would otherwise require polynomial long division. It allows us to factor the expression without going through the full division process.

43. How does the a³ + b³ formula relate to the concept of symmetry in mathematics?

The formula demonstrates a kind of algebraic symmetry. The roles of a and b can be interchanged in the formula without changing its validity, reflecting the symmetric nature of the sum of cubes.

44. Why isn't there a simple formula for a⁴ + b⁴ similar to a³ + b³?

Unlike a³ + b³, a⁴ + b⁴ doesn't have a simple factorization over real numbers. This is because the algebraic properties that allow the factorization of a³ + b³ don't extend to fourth powers in the same way.

45. How does the a³ + b³ formula relate to the concept of algebraic structures?

The formula demonstrates properties of polynomial rings, an important algebraic structure. It shows how certain polynomials can be factored within this structure, revealing deeper algebraic relationships.

46. Can the a³ + b³ formula be generalized to more than two terms?

The formula doesn't directly generalize to more than two terms. For sums of three or more cubes, different techniques are required, and there isn't a simple, universal formula like there is for a³ + b³.

47. How does the a³ + b³ formula compare to the completing the cube method?

While both deal with cubic terms, they serve different purposes. The a³ + b³ formula is for factoring a sum of cubes, while completing the cube is a method for solving certain cubic equations by transforming them into a standard form.

48. What's the historical significance of the a³ + b³ formula?

This formula has been known for centuries and played a role in the development of algebra. It was particularly important in early efforts to solve cubic equations, contributing to the advancement of mathematical understanding.

49. How can the a³ + b³ formula be used in problem-solving strategies?

In problem-solving, recognizing when to apply this formula can simplify complex expressions, making equations easier to solve. It's particularly useful in problems involving cubic terms or volume calculations.

50. What role does the a³ + b³ formula play in the study of polynomial equations?

This formula is crucial in the study of cubic equations. It provides a method for factoring certain types of cubic polynomials, which is essential in finding roots and understanding the behavior of these equations.

51. Can the a³ + b³ formula be applied in fields outside of pure mathematics?

Yes, this formula has applications in various fields, including physics (e.g., in calculations involving cubic volumes or third-power relationships) and computer science (in certain algorithms dealing with polynomial expressions).

52. How does the a³ + b³ formula contribute to the understanding of polynomial factorization?

This formula provides insight into the nature of polynomial factorization, showing that even seemingly simple expressions like a³ + b³ can have non-obvious factorizations. It demonstrates that not all polynomials factor into linear terms over real numbers.

53. What's the relationship between the a³ + b³ formula and the concept of irreducible polynomials?

The second factor in the a³ + b³ formula, a² - ab + b², is an example of an irreducible quadratic polynomial over real numbers. This illustrates the concept that some polynomials cannot be factored further without using complex numbers.

54. What insights does the a³ + b³ formula provide about the nature of cubic expressions?

The formula shows that cubic expressions can often be simplified or factored in non-obvious ways. It demonstrates that the sum of cubes, unlike the sum of squares, has a standard factorization, revealing the unique properties of cubic terms.

55. What role does pattern recognition play in understanding and applying the a³ + b³ formula?

Pattern recognition is crucial in identifying when the a³ + b³ formula can be applied. Recognizing the sum of cubes pattern in more complex expressions is a key skill in advanced algebraic manipulation and problem-solving.