Adjoint and Inverse of a Matrix

The adjoint and inverse of a matrix are two essential concepts in linear algebra. Before we learn the concept of the adjoint of a matrix, let's first understand what a matrix is. A matrix is a group of symbols organized in rows and columns to form a rectangle. The symbols may include real or complex numbers. Consequently, a m by n matrix, also known as a m x n matrix, is a system of m x n symbols arranged in a rectangular shape along m rows and n columns and bound by the brackets [ ]. The inverse of a matrix is utilized in GPS systems, where it is applied to analyze satellite signals and determine the precise location of a device. For image processing tasks like distortion correction and image scaling, matrix inverses are also crucial.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

1. Adjoint of a Matrix
2. Properties of the adjoint of a matrix
3. The inverse of a Matrix
4. Solved Examples Based on Adjoint of Matrix

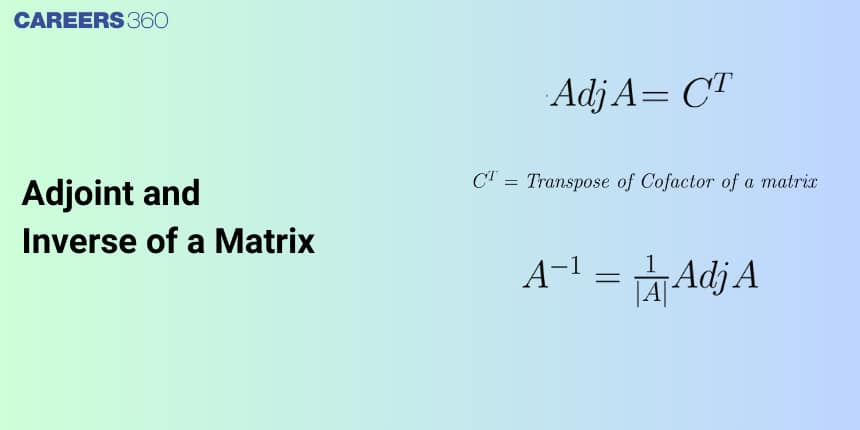
In this article, we will cover the concept of adjoint and inverse of matrix. This category falls under the broader category of Matrices, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main Exam (from 2013 to 2023), a total of 26 questions have been asked on this concept, including two in 2020, three in 2021, nine in 2022, and nine in 2023.

Adjoint of a Matrix

Adjoint of a matrix A is the transpose of the cofactor matrix of the matrix A. A Cofactor matrix of matrix A is a matrix that has the same order as that of A and has elements in place of $a_{ij}$
$\text{ let }A=\left[\begin{array}{lll}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]$
and let the cofactor of every element is
$\left[\begin{array}{lll}{C}_{11}& C_{12}& C_{13}\\ C_{21}& C_{22}& C_{23}\\ C_{31}& C_{32}& C_{33}\end{array}\right]$
then Adjoint of $\mathrm{A}$ is
$A^{\prime }={\left[\begin{array}{lll}{C}_{11}& C_{12}& C_{13}\\ C_{21}& C_{22}& C_{23}\\ C_{31}& C_{32}& C_{33}\end{array}\right]}^{\prime }=\left[\begin{array}{lll}{C}_{11}& C_{21}& C_{31}\\ C_{12}& C_{22}& C_{32}\\ C_{13}& C_{23}& C_{33}\end{array}\right]$

Properties of the adjoint of a matrix

1. If A is a square matrix of order n, then

$(\mathrm{Adj}\mathrm{A})\mathrm{A}=\mathrm{A}(\mathrm{Adj}\mathrm{A})=|\mathrm{A}|{\mathbb{I}}_{\mathrm{n}}$, or product of a matrix, and its adjoint is commutative.
Proof:
Let, $\mathrm{A}=\left[\begin{array}{lll}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]$, then adj $\mathrm{A}=\left[\begin{array}{lll}{A}_{11}& A_{21}& A_{31}\\ A_{12}& A_{22}& A_{32}\\ A_{13}& A_{23}& A_{33}\end{array}\right]$ where, $A_{ij}$ is co - factor of $a_{ij}$

Since the sum of the product of elements of a row (or a column) with corresponding cofactors is equal to $|\mathrm{A}|$ and otherwise zero, we have
$\mathrm{A}(\mathrm{adj}\mathrm{A})=\left[\begin{array}{ccc}|A|& 0& 0\\ 0& |A|& 0\\ 0& 0& |A|\end{array}\right]=|\mathrm{A}|\left[\begin{array}{lll}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]=|\mathrm{A}|\mathrm{I}$

If $A$ is a singular matrix of order $n$, then $(\mathrm{Adj}A)A=A(\mathrm{Adj}A)=0$ (null matrix) $(As|A|=0$ )
2. If $A$ is a non-singular square matrix of order $n$, then $|AdjA|=|A{|}^{n-1}$

Proof:
$A(\mathrm{Adj}A)=|A|I_n$

Taking determinants on both sides
$\begin{array}{rl}& |\mathrm{A}(\mathrm{Adj}\mathrm{A})|=||\mathrm{A}\left|{\mathrm{I}}_{\mathrm{n}}\right|\\ & |\mathrm{A}||(\mathrm{Adj}\mathrm{A})|=|\mathrm{A}{|}^{\mathrm{n}}\end{array}$

$|(\mathrm{adj}\mathrm{A})|=|\mathrm{A}{|}^{\mathrm{n}-1}$
3. If $A$ and $B$ are square matrices of order $n$, then, $\mathrm{adj}(AB)=(\mathrm{adj}B)(\mathrm{adj}A)$
4. If $\mathrm{A}$ is a square matrix of order $\mathrm{n}$, then, $(\mathrm{adj}\mathrm{A}{)}^{\prime }=\mathrm{adj}{\mathrm{A}}^{\prime }$
5. If $\mathrm{A}$ is a square a non-singular matrix of order $\mathrm{n}$, then $\mathrm{adj}(\mathrm{adj}\mathrm{A})=|\mathrm{A}{|}^{\mathrm{n}-2}\mathrm{A}$

Proof:
$A(\mathrm{adj}A)=|A|{\mathbb{I}}_n$
replace $\mathrm{A}$ by $\mathrm{adj}\mathrm{A}$, then
$(\mathrm{adj}\mathrm{A})(\mathrm{adj}(\mathrm{adj}\mathrm{A}))=|\mathrm{adj}A|{\mathbb{I}}_{\mathrm{n}}=|\mathrm{A}{|}^{\mathrm{n}-1}{\mathbb{I}}_{\mathrm{n}}$
Pre - multiplying both sides by matrix $\mathrm{A}$, then
$\mathrm{A}(\mathrm{adj}\mathrm{A})(\mathrm{adj}(\mathrm{adj}\mathrm{A}))=\mathrm{A}{\mathbb{I}}_{\mathrm{n}}|\mathrm{A}{|}^{\mathrm{n}-1}=\mathrm{A}|\mathrm{A}{|}^{\mathrm{n}-1}$
$|\mathrm{A}|{\mathbb{I}}_{\mathrm{n}}(\mathrm{adj}(\mathrm{adj}\mathrm{A}))=\mathrm{A}|\mathrm{A}{|}^{\mathrm{n}-1}$
$(\mathrm{adj}(\mathrm{adj}A))=A|A{|}^{\mathrm{n}-2}=|\mathrm{A}{|}^{\mathrm{n}-2}\mathrm{A}$
6. If $\mathrm{A}$ is a non-singular square matrix, then, $|\mathrm{adj}(\mathrm{adj}\mathrm{A})|=|\mathrm{A}{|}^{(\mathrm{n}-1{)}^2}$

Proof: from the previous property, we know that
$\mathrm{adj}(\mathrm{adj}\mathrm{A})=|\mathrm{A}{|}^{(\mathrm{n}-2)}\mathrm{A}$

Taking determinants on both sides,
$|\mathrm{adj}(\mathrm{adj}\mathrm{A})|={{||\mathrm{A}|}^{(\mathrm{n}-2)}\mathrm{A}|=|\mathrm{A}|}^{\mathrm{n}(\mathrm{n}-2)}|\mathrm{A}|=|\mathrm{A}{|}^{(\mathrm{n}-1{)}^2}$
(using $|kA|=k^n|A|$ )
7. If $A$ is a square matrix of order $n$ and $m$ is any natural number, then $\left(\mathrm{adj}{A}^m\right)=(\mathrm{adj}A{)}^m$
8. If $A$ is a square matrix of order $n$ and $k$ is a scalar, then, $\mathrm{adj}(kA)=k^{n-1}\cdot (\mathrm{adj}A)$

The inverse of a Matrix

A non-singular square matrix A is said to be invertible if there exists a non-singular square matrix B such that

AB = I = BA

and the matrix B is called the inverse of matrix A. Clearly, B should also have the same order as A.

Hence, ${\mathrm{A}}^{-1}=\mathrm{B}\iff \mathrm{AB}={\mathbb{I}}_{\mathrm{n}}=\mathrm{BA}$
The formula for the inverse of $\mathrm{A}$
We know
$\begin{array}{rl}& \mathrm{A}(\mathrm{adjA})=|\mathrm{A}|{\mathbb{I}}_{\mathrm{n}}\\ & \text{ Multiplying both sides by }{\mathrm{A}}^{-1}\\ & \Rightarrow {\mathrm{A}}^{-1}\mathrm{A}(\mathrm{adj}\mathrm{A})={\mathrm{A}}^{-1}{\mathbb{I}}_{\mathrm{n}}|\mathrm{A}|\\ & \Rightarrow {\mathbb{I}}_{\mathrm{n}}(\mathrm{adjA})={\mathrm{A}}^{-1}|\mathrm{A}|{\mathbb{I}}_{\mathrm{n}}(\text{ As }{A}^{-1}\cdot A=I)\\ & {\mathrm{A}}^{-1}=\frac{\mathrm{adj}\mathrm{A}}{|\mathrm{A}|}\end{array}$

Hence, ${\mathrm{A}}^{-1}=\mathrm{B}\iff \mathrm{AB}={\mathbb{I}}_{\mathrm{n}}=\mathrm{BA}$

The formula for the inverse of A is ${\mathrm{A}}^{-1}=\frac{\mathrm{adj}\mathrm{A}}{|\mathrm{A}|}$ .

Recommended Video Based on Adjoint of Matrix:

Solved Examples Based on Adjoint of Matrix

Example 1: Let $\mathrm{A}$ be a matrix of order $3\times 3$ and $\det (\mathrm{A})=2$. Then $\det (\det (\mathrm{A})\mathrm{adj}\left(5\mathrm{adj}\left({\mathrm{A}}^3\right)\right))\text{ is equal to }$ $$ [JEE Main 2022]

Solution:
$\begin{array}{rl}& \det \left(2\mathrm{adj}\left(5\mathrm{adj}\left({\mathrm{A}}^3\right)\right)\right)\\ & =2^3\left|\mathrm{adj}\left(5\mathrm{adj}\left({\mathrm{A}}^3\right)\right)\right|\\ & =2^3{\left|5\mathrm{adj}\left({\mathrm{A}}^3\right)\right|}^2\\ & =2^3{\left(5^3\left|\mathrm{adj}\left({\mathrm{A}}^3\right)\right|\right)}^2\\ & =2^3{5}^6{\left({\left|{\mathrm{A}}^3\right|}^2\right)}^2=2^3{5}^6|\mathrm{A}{|}^{12}=2^3{5}^6{2}^{12}\\ & =2^{15}{5}^6=2^9{10}^6=512\times {10}^6\end{array}$

Hence, the required answer is $512\times {10}^6$

Example 2: Let $\mathrm{S}=\{\sqrt{\mathrm{n}}:1⩽\mathrm{n}⩽50$ and $\mathrm{n}$ is odd $\}$.
Let $\mathrm{a}\in \mathrm{S}$ and $\mathrm{A}=\left[\begin{array}{ccc}1& 0& a\\ -1& 1& 0\\ -a& 0& 1\end{array}\right]$
If $\sum _{aϵS}\det (\mathrm{adj}A)=100\lambda$, then $\lambda$ is equal to : [JEE Main 2022]

Solution
$\begin{array}{rl}& \mathrm{S}=\{\sqrt{\mathrm{n}}:1⩽\mathrm{n}⩽50\text{ and }\mathrm{n}\text{ is odd }\}\\ & \mathrm{A}=\left[\begin{array}{ccc}1& 0& a\\ -1& 1& 0\\ -a& 0& 1\end{array}\right]\end{array}$
$\mathrm{Det}(A)=1+a(0+a)=a^2+1$
$\sum _{\mathrm{a}\epsilon \mathrm{s}}\det (\mathrm{Adj}\mathrm{A})=100\lambda$
$\sum _{a\in s}{(a^2+1)}^2=100\lambda$
$\sum _{\mathrm{n}=\text{ odd }}(\mathrm{n}+1{)}^2=100\lambda$
$2^2+4^2+6^2+\cdots {50}^2=100\lambda$
$2^2(1^2+2^2+\cdots +{25}^2)=100\lambda$
$\frac{4\times 25\times 26\times 51}{6}=100\lambda$
$\lambda =221$

Hence, the required answer is 221.

Example 3: Let $\mathrm{A}$ be a $3\times 3$ invertible matrix. If $|\mathrm{adj}(24\mathrm{A})|=|\mathrm{adj}(3\mathrm{adj}(2\mathrm{A}))|$, then $|\mathrm{A}{|}^2$ is equal to : [JEE Main 2022]
$\begin{array}{rl}& \text{ Solution: }\\ & \begin{array}{r}|\mathrm{adj}(24\cdot \mathrm{A})|=|\mathrm{adj}3(\mathrm{adj}2\mathrm{A})|\\ \begin{array}{c}\Rightarrow |24\mathrm{A}{|}^2=|3\mathrm{adj}(2A){|}^2\end{array}\\ \begin{array}{c}\Rightarrow {\left({24}^3|\mathrm{A}|\right)}^2={(3^3|\mathrm{adj}(2\mathrm{A})|)}^2\\ =3^6{\left(|2\mathrm{A}{|}^2\right)}^2\\ \Rightarrow {24}^6|\mathrm{A}{|}^2=3^6\times 2^{12}\cdot |\mathrm{A}{|}^4\end{array}\\ \Rightarrow |\mathrm{A}{|}^2=\frac{{24}^6}{3^6\times 2^{12}}=64\end{array}\end{array}$

Hence, the required answer is 64.

Example 4: Let A be a $3\times 3$ real matrix. If $\det (2\mathrm{Adj}(2\mathrm{Adj}(\mathrm{Adj}(2A))))=2^{41}$, then the value of $\det \left(A^2\right)$ equals $$ [JEE Main 2021]

Solution:

As for any square matrix P of order n and a scalar k,

$\begin{array}{rl}& |kP|=k^n|P|--(i)\\ & \text{ and }|\mathrm{adj}P|=|P{|}^{n-1}---(\text{ ii })\\ & \text{ and }|\mathrm{adj}(\mathrm{adj}P)|=|P{|}^{n-2}---(\text{ iii })\\ & \therefore |\mathrm{adj}(\mathrm{aadj}(\mathrm{adj}(2A)))|\\ & =2^3|\mathrm{adj}(2\mathrm{adj}(\mathrm{adj}(2A)))|\\ & =2^3\cdot |2\mathrm{adj}(\mathrm{adj}(2A)){|}^2\\ & =2^3\cdot {[2^3|\mathrm{adj}(\mathrm{adj}(2A))|]}^2\\ & =2^3\cdot 2^6\cdot [\mathrm{adj}(\mathrm{adj}(2A)){]}^2\\ & =2^9\cdot {\left[|2A{|}^{2^2}\right]}^2\\ & =2^9\cdot {\left[{\left(2^3|A|\right)}^4\right]}^2\\ & =2^9\cdot 2^{24}\cdot |A{|}^8\end{array}$

Given that this equals $2^{41}$
$\begin{array}{rl}& \Rightarrow 2^{33}\cdot |A{|}^8=2^{41}\\ & \Rightarrow |A{|}^8=2^8\\ & \Rightarrow |A|=2\\ & \Rightarrow |A{|}^2=4\end{array}$

Hence, the required answer is 4.

Example 5: Consider a $\mathrm{A}=\left[\begin{array}{ccc}\alpha & \beta & \gamma \\ {\alpha }^2& {\beta }^2& {\gamma }^2\\ \beta +\gamma & \gamma +\alpha & \alpha +\beta \end{array}\right]$, where $\alpha ,\beta ,\gamma$ are three distinct natural numbers. If $\frac{\det (\mathrm{adj}(\mathrm{adj}(\mathrm{adj}(\mathrm{adj}A))))}{(\alpha -\beta {)}^{16}(\beta -\gamma {)}^{16}(\gamma -\alpha {)}^{16}}=2^{32}\times 3^{16}$, then the number of such 3 - tuples $(\alpha ,\beta ,\gamma )$ is [JEE Main 2022]

Solution:

$\begin{array}{rl}& |\mathrm{A}|=\left|\begin{array}{ccc}\alpha & \beta & \gamma \\ {\alpha }^2& {\beta }^2& {\gamma }^2\\ \beta +\gamma & \gamma +\alpha & \alpha +\beta \end{array}\right|\\ & {\mathrm{R}}_3\to {\mathrm{R}}_1+{\mathrm{R}}_3\\ & =\left|\begin{array}{ccc}\alpha & \beta & \gamma \\ {\alpha }^2& {\beta }^2& {\gamma }^2\\ \alpha +\beta +\gamma & \alpha +\beta +\gamma & \alpha +\beta +\gamma \end{array}\right|\\ & =(\alpha +\beta +{\gamma }^{\ast })\left|\begin{array}{ccc}\alpha & \beta & \gamma \\ {\alpha }^2& {\beta }^2& {\gamma }^2\\ 1& 1& 1\end{array}\right|\\ & =(\alpha +\beta +\gamma )(\alpha -\beta )(\beta -\gamma )(\gamma -\alpha )\\ & \text{ Now }\frac{|\mathrm{adj}(\mathrm{adj}(\mathrm{adj}(\mathrm{adj}\mathrm{A})))|}{(\alpha -\beta {)}^{16}(\beta -\gamma {)}^{16}(\gamma -\alpha {)}^{16}}=2^{32}\cdot 3^{16}\\ & \Rightarrow \frac{|\mathrm{A}{|}^{(\mathrm{n}-1{)}^4}}{(\alpha -\beta {)}^{16}(\beta -\gamma {)}^{16}(\gamma -\alpha {)}^{16}}=2^{3^2\cdot 3^{16}}\\ & \Rightarrow {(\alpha +{\beta }^{\beta +\gamma })}^{16}=2^{3^2}\cdot 3^{16}\\ & \Rightarrow \alpha +\beta +\gamma =4\cdot 3=12\\ & \Rightarrow \alpha +\beta +\gamma =12\end{array}$

Totel Natural number solutions of this equation ${}^{12-1}{\mathrm{C}}_{3-1}={}^{11}{\mathrm{C}}_2$ $=55$
Removing cases where $\alpha ,\beta ,\gamma$ are not distinat
$\begin{array}{rl}& \alpha =\beta =\gamma =4\\ & \alpha =\beta \Rightarrow 4\text{ cases }(1,1,10),(2,2,8),(3,3,6),(5,5,2)\end{array}$

Similarly 4 cases each for $\beta =\gamma$ and $\alpha =\gamma$
$55-1-4-4-4=42$
Hence, the required answer is 42.