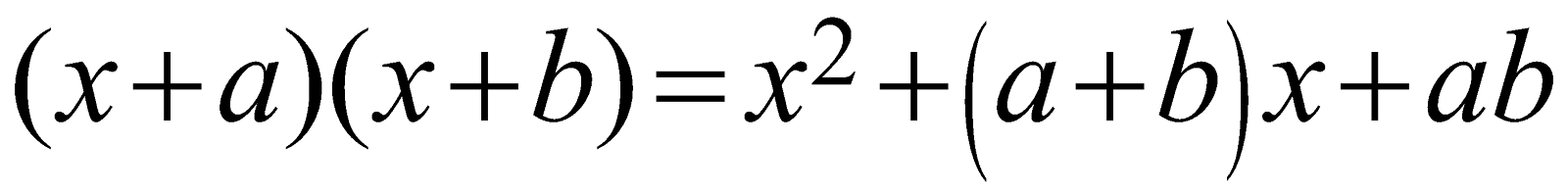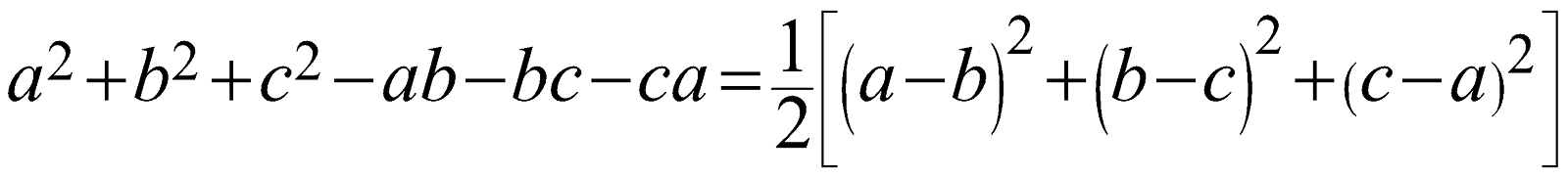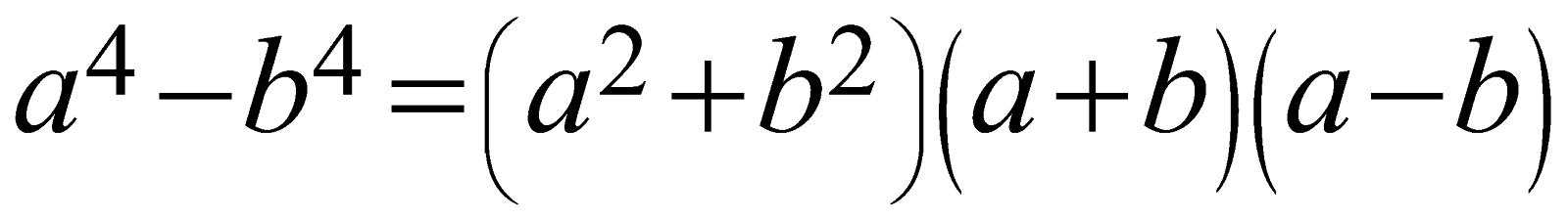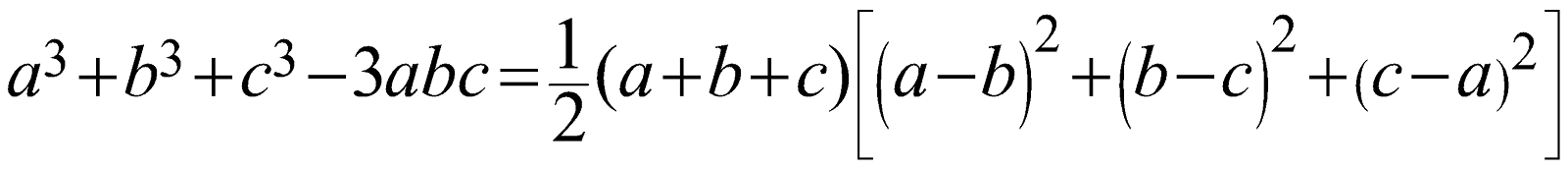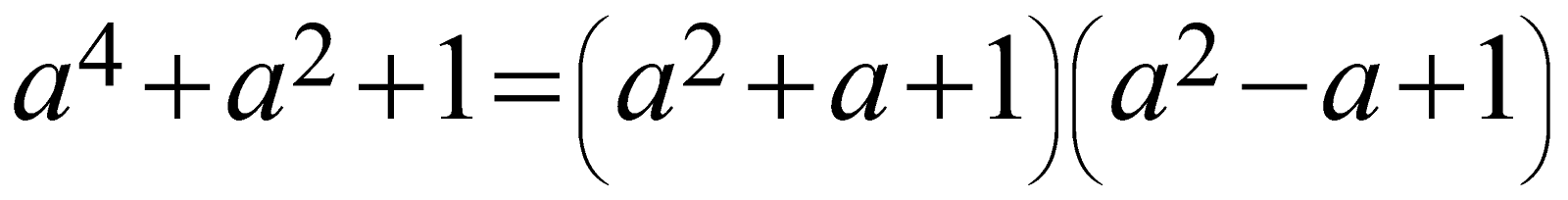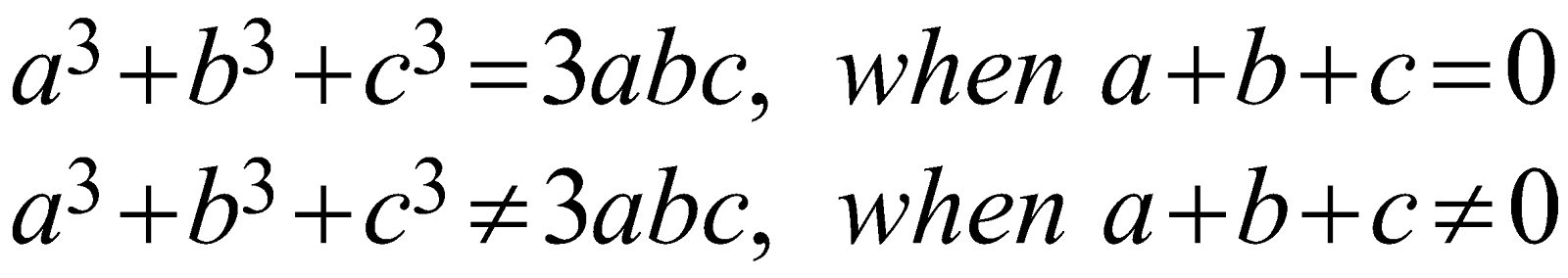Algebraic Expressions Questions | Algebraic Expressions Questions with Solutions

Algebraic Expressions Questions

Edited By Team Careers360 | Updated on Jul 02, 2025 05:21 PM IST

The concept of “algebraic identities” will be clear to you, once you have an idea about the defining characteristics of “expressions”, “identities”, etc. The terms “algebraic expressions”, “algebraic equations”, and “algebraic identities” have the common word “algebraic”.

The fact is that all “mathematical expressions” are not “algebraic expressions”. Likewise, “identities” encompass the “algebraic identities” along with the other types of identities. Thus it is important to identify when an “expression” becomes an “algebraic expression”, and when an “equation” becomes an “algebraic equation”. You will here, explore the difference between an “identity” and an “algebraic identity”. Also, you will get an idea about the functionalities of “algebraic identities”

This Story also Contains

what Are The Types Of Mathematical Expressions?
What Are The Types Of Equations?
What Are The Types Of Identities?
What Are Algebraic Polynomials?
Chart Of Algebraic Identities

It is presumed that the terms “constants”, “Variables”, “and coefficients”, and mathematical operations like multiplication, division, subtraction, addition, and exponentiation are known to you.

Let us dive into this article to grasp the sound idea about “algebraic identities”.

what Are The Types Of Mathematical Expressions?

As such the symbolic arrangement of any combination of mathematical operations like addition, division, multiplication, subtraction, and exponentiation as specified by the corresponding mathematical operators, as per any valid mathematical statement, is termed the “mathematical expression”.

Following are some of the different types of mathematical expressions.

Numeric Expressions: The mathematical expression that consists of no “Variables” and hence no “coefficients”, but only numerical values or “constants” is called a “numeric expression. The mathematical expression \[\frac{\sqrt{3}}{4}+2\] 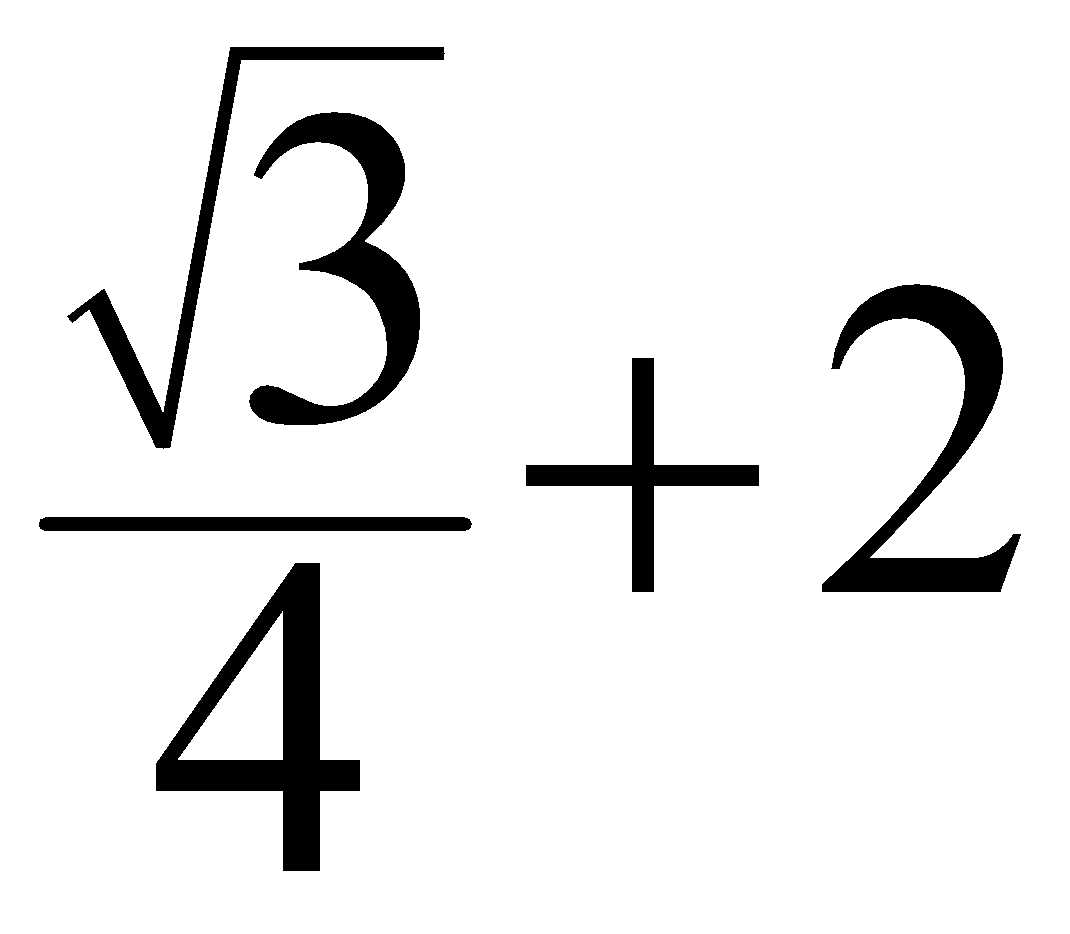is a numeric expression.
Algebraic Expressions: The mathematical expression that contains “algebraic Variables”, “coefficients”, “constants” in any combination is called an “algebraic expression.

Note that the algebraic expressions”. \[2{{x}^{3}}+a,\ \ {{y}^{2}}+3\] 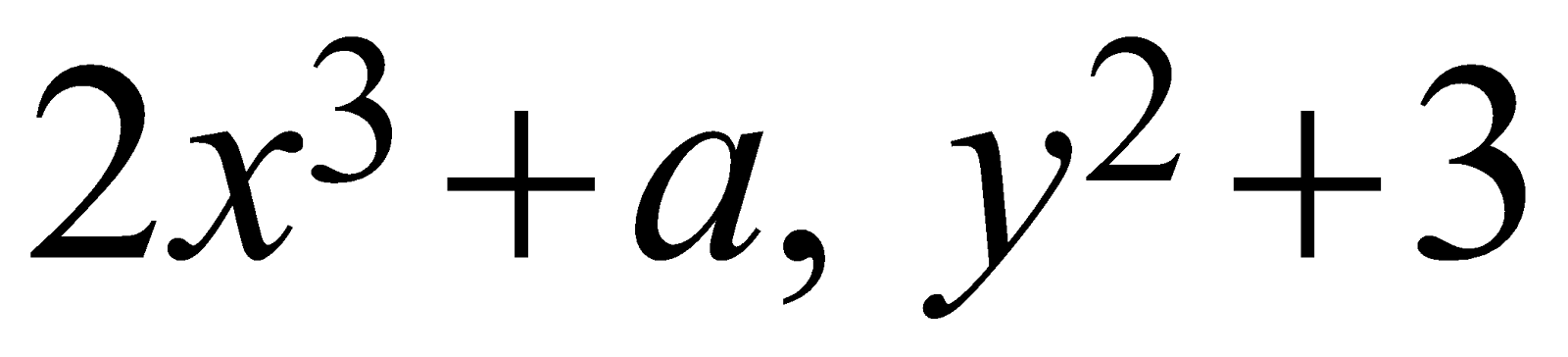1706529961393

Trigonometric Expressions: The mathematical expression that has “trigonometric terms” in “Variables”, “constants” in any combination is called a “trigonometric expression.

See that the mathematical expressions \[2{{\cos }^{3}}\theta +a,\ \ {{\cos }^{2}}\frac{\pi }{2}+3\] 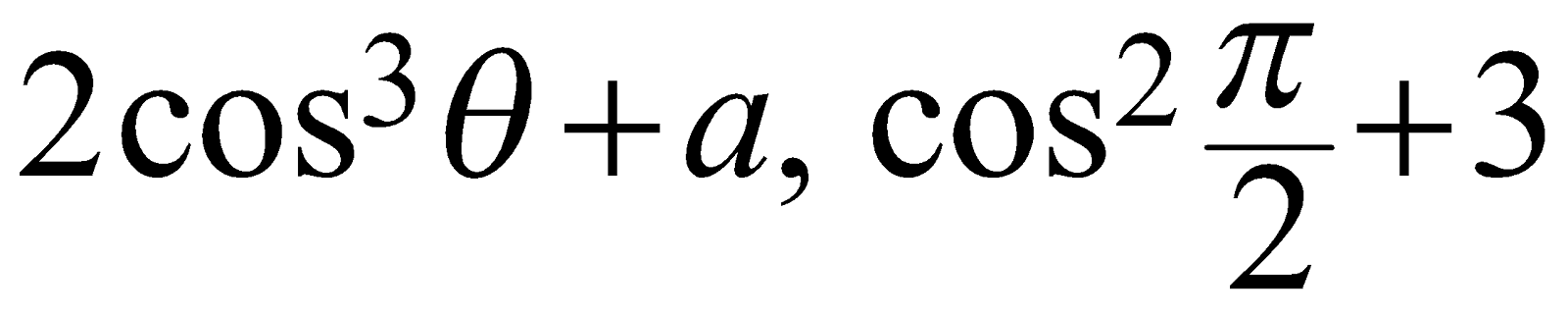1706529960317 are “trigonometric expressions”.

What Are The Types Of Equations?

An “equation” has the “equal to symbol” represented as “=” to join any two expressions or an algebraic expression to any constant. An algebraic equation, essentially, infers that the mathematical terms on either side of the “=” symbol are equivalent.

Following are some of the different types of equations.

Algebraic Equations: The mathematical equation that contains “algebraic Variables” with or without “coefficients”, equal to other algebraic variables or “constants” in any combination is called an “algebraic Equation. Note that the mathematical equations \[\frac{2}{5}{{x}^{3}}+a{{y}^{2}}=b,\ \ 5{{y}^{2}}+3=0\] 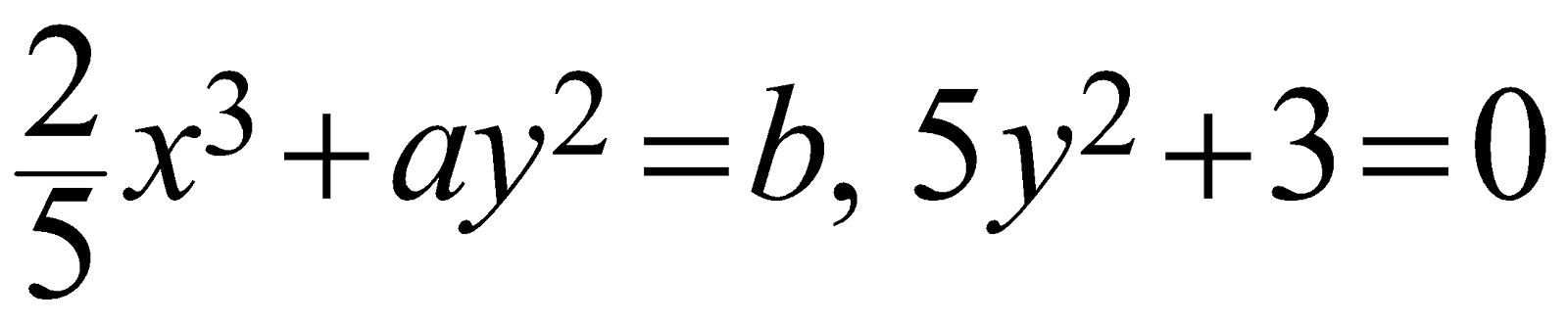are “algebraic Equations”.
Trigonometric Equations: The mathematical equation that has “trigonometric terms” in “Variables”, “constants” in any combination is called a “trigonometric Equation.

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

See that the mathematical Equations \[2{{\cos }^{3}}\theta +a=b,\ \ 4{{\cos }^{2}}\frac{\pi }{2}-1=\sin \alpha \] are “trigonometric Equations”.

What Are The Types Of Identities?

You name those mathematical entities as “Identities” which are correct for any value of the variables present in one or both the expressions on either side of the “=”.

Following are some of the different types of Identities.

Algebraic Identities: The identity involving only the algebraic expressions or an algebraic expression and any constant, such that on putting any value in the variable, the equality holds good, is called an algebraic identity.

Note that these “algebraic Identities”. \[{{(x+y)}^{2}}={{x}^{2}}+{{y}^{2}}+2xy,\ \ {{(x-y)}^{2}}={{x}^{2}}+{{y}^{2}}-2xy\] 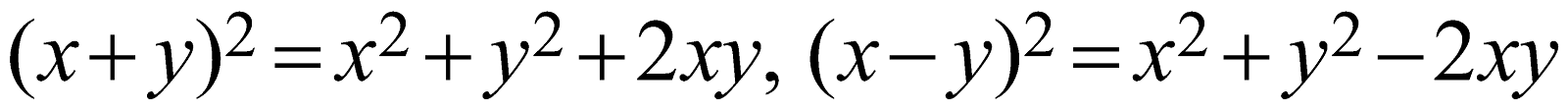1706529961972

Trigonometric Identities: The identity that has “trigonometric terms” in “Variables”, “constants” in any combination is called a “trigonometric Equation.

See that these trigonometric Identities.\[{{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1,\ \ 1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta \]. 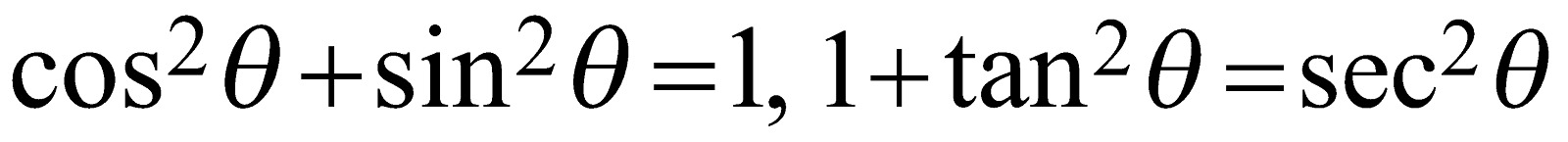1706529961741

Mensuration Identities: The identity that has “mensuration terms” in “Variables”, and “constants” in any combination is called a “mensuration Equation.

Note the following “mensuration Identities”.\[\begin{align}

{{a}^{2}}+{{b}^{2}}={{c}^{2}},\ \ \text{for any right angled triangle} \\

area=sid{{e}^{2}},\ \ \text{for any square} \\

\end{align}\]

1706529962934

What Are The Algebraic Identities Important?

The algebraic identities are important from the mathematical point of view and the following are some of the reasons.

An algebraic identity cannot have a finite number of solutions, as it is true for an infinite number of values that you put in place of its variables.
For the simplification of algebraic polynomials, they are useful.
They are beneficial in the factorization of algebraic expression
They find applications in solving any algebraic equation.
You also get some conditional algebraic identities. For example \[{{a}^{3}}+{{b}^{3}}+{{c}^{3}}=3abc,\quad when\ \ a+b+c=0\]

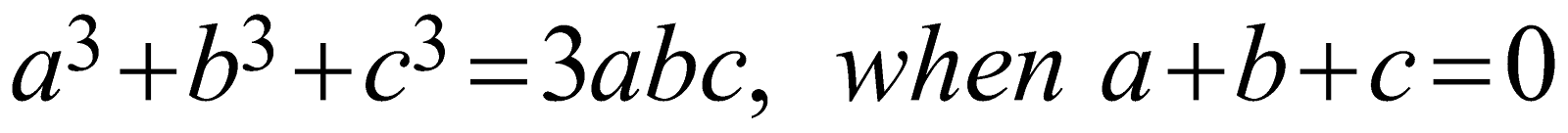
1706529961863

What Are Algebraic Polynomials?

You may come across expressions or equations which involve only the non-negative integral power of variables but may have any integral coefficients and constants. These algebraic entities are called algebraic polynomials

The examples of algebraic polynomials are the following.

\[{{(a+b)}^{4}},\ \ {{p}^{2}}+{{q}^{2}}+2ab,\ \ {{a}^{2}}+{{b}^{2}}+2\sqrt{3}\]

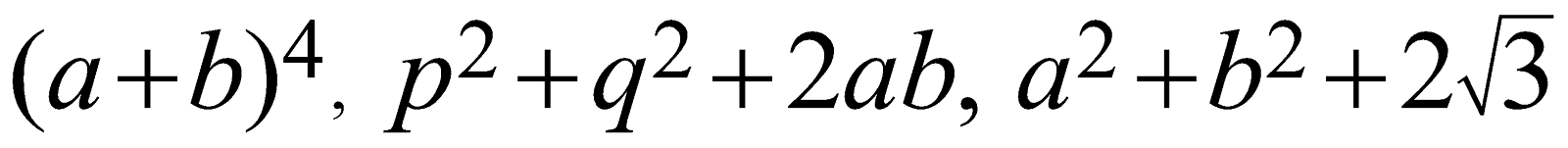
1706529960557

Chart Of Identities Of Factorization Of Polynomials

As you find the algebraic identities useful to factorize, and simplify the algebraic expressions, here is your quick reference chart for some of the algebraic identities that you will use for factorization of the polynomials, whenever necessary.

Algebraic Identities
Description	Formulae
Whole square of the sum of any two variables	\[{{(a+b)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab\]
Whole square of the difference between any two variables.	\[{{(a-b)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\]
Difference between any two squares	\[{{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)\]
Whole square of the sum of any three variables	\[{{(a+b+c)}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc+2ca\]
Whole cube of the sum of any two variables	\[{{(a+b)}^{3}}={{a}^{3}}+{{b}^{3}}+3a{{b}^{2}}+3{{a}^{2}}b\]
Whole cube of the difference between any two variables.	\[{{(a-b)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\]
Sum of any two cubes	\[{{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\]
Difference between any two cubes	\[{{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\]
Whole cube of the sum of any three variables	\[{{(a+b+c)}^{3}}={{a}^{3}}+{{b}^{3}}+{{c}^{3}}+3\left( a+b \right)\left( b+c \right)\left( c+a \right)\]

Chart Of Algebraic Identities

For simplification of algebraic terms, solving any algebraic equation or factorization of an algebraic expression, the following are some of the useful algebraic identities.

Algebraic Identities

\[(x+a)(x+b)={{x}^{2}}+\left( a+b \right)x+ab\]

1706529962472

\[{{a}^{2}}+{{b}^{2}}+{{c}^{2}}-ab-bc-ca=\frac{1}{2}\left[ {{\left( a-b \right)}^{2}}+{{\left( b-c \right)}^{2}}+{{\left( c-a \right)}^{2}} \right]\]

1706529962561

\[{{a}^{4}}-{{b}^{4}}=\left( {{a}^{2}}+{{b}^{2}} \right)\left( a+b \right)\left( a-b \right)\]

1706529962641

\[{{a}^{3}}+{{b}^{3}}+{{c}^{3}}-3abc=\frac{1}{2}(a+b+c)\left[ {{\left( a-b \right)}^{2}}+{{\left( b-c \right)}^{2}}+{{\left( c-a \right)}^{2}} \right]\]

1706529963099

\[{{a}^{4}}+{{a}^{2}}+1=\left( {{a}^{2}}+a+1 \right)\left( {{a}^{2}}-a+1 \right)\]

1706529963219

\[\begin{align}

{{a}^{3}}+{{b}^{3}}+{{c}^{3}}=3abc,\quad when\ \ a+b+c=0 \\

{{a}^{3}}+{{b}^{3}}+{{c}^{3}}\ne 3abc,\quad when\ \ a+b+c\ne 0 \\

\end{align}\]

1706529964190

\[a-b=\left( \sqrt{a}+\sqrt{b} \right)\left( \sqrt{a}-\sqrt{b} \right),\ \ for\ a,b>0\]

1706529963728

Frequently Asked Questions (FAQs)

1. What is the FOIL method and when is it used?

FOIL is a mnemonic for multiplying two binomials: First, Outer, Inner, Last. For example, (x + 2)(x + 3):

2. How do you factor a quadratic expression?

To factor a quadratic expression (ax² + bx + c):

3. How do you multiply polynomials?

To multiply polynomials:

4. What is the difference between factoring and expanding?

Factoring and expanding are opposite processes:

5. How do you add or subtract polynomials?

To add or subtract polynomials, combine like terms. Like terms have the same variables raised to the same powers. For example:

6. What's the difference between a monomial, binomial, and trinomial?

These terms refer to the number of terms in a polynomial:

7. How do you determine the degree of a polynomial?

The degree of a polynomial is the highest power of the variable in the polynomial. For a polynomial with multiple variables, it's the highest sum of exponents in any term. For example:

8. What is the standard form of a polynomial?

The standard form of a polynomial is when terms are arranged in descending order of degree, from highest to lowest. For example, 5x³ - 2x² + 4x - 7 is in standard form. This arrangement makes it easier to identify the degree and leading term of the polynomial.

9. What is a zero of a polynomial?

A zero (or root) of a polynomial is a value of x that makes the polynomial equal to zero. For example, in x² - 4 = 0, the zeros are 2 and -2 because when x = 2 or x = -2, the polynomial equals zero. Finding zeros is crucial for solving polynomial equations and understanding the behavior of polynomial functions.

10. How do you identify terms in an algebraic expression?

Terms in an algebraic expression are parts separated by addition or subtraction signs. Each term can be a constant, a variable, or a combination of constants and variables multiplied together. For example, in the expression 3x² + 2x - 5, there are three terms: 3x², 2x, and -5.

11. What is the discriminant of a quadratic equation and what does it tell us?

The discriminant of a quadratic equation ax² + bx + c = 0 is given by b² - 4ac. It provides information about the roots:

12. What is the difference between a polynomial equation and a polynomial inequality?

A polynomial equation sets a polynomial expression equal to zero or another polynomial, like x² + 2x - 3 = 0. It asks for specific x-values that make the equation true.

13. How do you find the axis of symmetry for a quadratic function?

For a quadratic function f(x) = ax² + bx + c, the axis of symmetry is a vertical line given by x = -b/(2a). This line passes through the vertex of the parabola. To find it:

14. What is the difference between a polynomial function and a polynomial expression?

A polynomial expression is a mathematical phrase involving variables and coefficients, like 2x² + 3x - 5. A polynomial function, on the other hand, assigns each input value (x) to a unique output value (y), often written as f(x) = 2x² + 3x - 5. The function can be graphed and has properties like domain and range.

15. How do you use the rational root theorem to find possible roots of a polynomial?

The Rational Root Theorem states that if a polynomial equation anxⁿ + an-1xⁿ⁻¹ + ... + a1x + a0 = 0 with integer coefficients has a rational solution, it will be of the form ±p/q, where:

16. What is the leading coefficient and why is it important?

The leading coefficient is the coefficient of the term with the highest degree in a polynomial. For example, in 3x⁴ - 2x² + 5, the leading coefficient is 3. It's important because:

17. How do you determine if a polynomial is even or odd?

A polynomial function f(x) is:

18. What is the relationship between factors and zeros of a polynomial?

There's a direct relationship between factors and zeros of a polynomial:

19. How do you use synthetic division to divide polynomials?

Synthetic division is a shortcut method for dividing a polynomial by a linear factor (x - a):

20. What is the Remainder Theorem and how is it used?

The Remainder Theorem states that the remainder of a polynomial p(x) divided by (x - a) is equal to p(a). This means you can find the remainder by simply evaluating the polynomial at x = a. It's useful for checking if (x - a) is a factor of the polynomial (the remainder would be zero) and for polynomial long division.

21. What is an algebraic expression?

An algebraic expression is a combination of variables, numbers, and mathematical operations. It can include letters representing unknown values, constants, and symbols for addition, subtraction, multiplication, or division. Unlike equations, algebraic expressions don't have an equals sign and don't represent a specific value.

22. How do you use the conjugate root theorem?

The Conjugate Root Theorem states that if a + bi is a complex root of a polynomial with real coefficients, then its complex conjugate a - bi is also a root. This means:

23. What is the relationship between complex roots and the graph of a polynomial?

Complex roots of a polynomial don't appear on its graph in the real coordinate system, but they influence the shape:

24. What is the significance of the Rational Root Theorem in factoring polynomials?

The Rational Root Theorem is significant in factoring polynomials because:

25. How do you find the y-intercept of a polynomial function?

The y-intercept of a polynomial function is the point where the graph crosses the y-axis. To find it, substitute x = 0 into the polynomial. For example, if f(x) = x³ - 2x² + 3x - 4, the y-intercept is f(0) = 0³ - 2(0)² + 3(0) - 4 = -4. So the y-intercept is (0, -4).

26. How do you graph a polynomial function?

To graph a polynomial function:

27. What is the relationship between the degree of a polynomial and its graph?

The degree of a polynomial relates to its graph in several ways:

28. How do you find the multiplicity of a root in a polynomial?

The multiplicity of a root is the number of times a factor appears in the factored form of the polynomial. To find it:

29. How do you use Descartes' Rule of Signs?

Descartes' Rule of Signs helps determine the possible number of positive and negative real roots of a polynomial:

30. What is the fundamental theorem of algebra?

The Fundamental Theorem of Algebra states that every non-constant polynomial with complex coefficients has at least one complex root. This implies that:

31. What is polynomial long division and when is it used?

Polynomial long division is a method to divide one polynomial by another. It's similar to regular long division but with polynomials. It's used to:

32. How do you determine the end behavior of a polynomial function?

To determine the end behavior of a polynomial function:

33. How do you use Vieta's formulas for polynomials?

Vieta's formulas relate the coefficients of a polynomial to sums and products of its roots. For a cubic equation x³ + ax² + bx + c = 0 with roots r, s, and t:

34. How do you solve a system of polynomial equations?

To solve a system of polynomial equations:

35. What is the relationship between the coefficients and roots of a polynomial?

The relationship between coefficients and roots of a polynomial is described by Vieta's formulas: