Algebraic Operations on Complex Numbers with Examples
A complex number is any number that can be in the form of a + bi, where a and b are real figures( a, b ∈ R), i is the imaginary unit, and $i^{2}=-1$.
Let us say 7+ 2i is a complex number, where 7 is a real number and 2i is an imaginary number. So, the combination of both the real number and the imaginary number will be a complex number. There can be four types of algebraic operations on complex figures which are mentioned below. The four fundamental operations in algebra on complex figures include
JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days
JEE Main 2025: Maths Formulas | Study Materials
JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics
- Addition Of Complex Numbers (+)
- $z_1+z_2=z$
- $z_1+z_2=z_2+z_1$
- $\lgroup\:z_1+z_2\rgroup+z_3=z_1+\lgroup\:z_2+z_3\rgroup$
- $z+\lgroup\:-z\rgroup=0$
- $\lgroup\:a+ib\rgroup+\lgroup\:0+i0\rgroup=a+ib$
- Subtraction Of Complex Numbers(-)
- Examples:-
- Multiplication Of Complex Numbers(*)
- Examples:-
- $z_1*z_2=z$
- $z_1*z_2=z_2*z_1$
- $z_1*\lgroup\:z_2*z_3\rgroup=\lgroup\:z_1*z_2\rgroup*z_3$
- $z_1*\lgroup\:z_2+z_3\rgroup=z_1*z_2+z_1*z_3$
- Division Of Complex Numbers (/)
- $z_1=c_1+id_1$
- and $z_2=c_2+id_2$
- then the quotient of $\frac{z_1}{z_2}$ is equal to,
- $\frac{z_1}{z_2}=z_1*\frac{1}{z_2}$
-
Addition (+)
-
Subtraction (-)
-
Multiplication (*)
-
Division (/)
Addition Of Complex Numbers (+)
Let us say that z1 and z2 are the two complex numbers
$z_1=\lgroup\:a+ib\rgroup$
$z_2=\lgroup\:c+id\rgroup$
On addition, these two complex numbers will be equal to
$z_1+z_2=\lgroup\:a+ib\rgroup+\lgroup\:c+id\rgroup$
$=\lgroup\:a+c\rgroup+i\lgroup\:b+d\rgroup$
Which gives another complex number whose real part is Re( z1) + Re( z2) = a+ c and the imaginary part of the new complex number = Im( z1) + Im( z2) = b + d.
Example: $\lgroup2+3i\rgroup+\lgroup2+2i\rgroup=\lgroup2+2\rgroup+\lgroup3+2\rgroup\:i=4+5i$
Properties Of Addition Of Complex Numbers
| Name of the Property | Description | Expression |
| Closure property | The addition of any two complex numbers gives the complex number | $z_1+z_2=z$ |
| Commutative property | The order of addition of any two complex numbers does not change the result ( both sides are equal) | $z_1+z_2=z_2+z_1$ |
| Associative property | Regrouping any three complex numbers, and then adding them, does not change the result ( L.H.S=R.H.S) | $\lgroup\:z_1+z_2\rgroup+z_3=z_1+\lgroup\:z_2+z_3\rgroup$ |
| Additive inverse property | Let us say that z = a+ib is a complex number, then from the additive inverse property, -z = -a – ib which is equal to zero | $z+\lgroup\:-z\rgroup=0$
|
| Additive identity | Adding a value to any complex number the results is the same complex number, then it is called the additive identity | $\lgroup\:a+ib\rgroup+\lgroup\:0+i0\rgroup=a+ib$
|
Subtraction Of Complex Numbers(-)
Let us say that z1 and z2 are two complex numbers...
$z_1=\lgroup\:a-ib\rgroup$
$z_2=\lgroup\:c-id\rgroup$
On deduction of these two complex numbers will be equal to
$z_1-z_2=\lgroup\:a-ib\rgroup-\lgroup\:c-id\rgroup$
$=\lgroup\:a-c\rgroup-i\lgroup\:b-d\rgroup$
Which gives another complex number whose real part of the new complex number is Re(z1) - Re(z2) = [a - c] and the imaginary part of the new complex number = Im(Z1) - Im(Z2) = [b - d].
Examples:-
-
$\lgroup6+10i\rgroup-\lgroup10+3i\rgroup=\lgroup6-10\rgroup+\lgroup10-3\rgroup\:i=-4+7i$
-
$\lgroup2+3i\rgroup-\lgroup2+2i\rgroup=\lgroup2-2\rgroup+\lgroup3-2\rgroup\:i=-0+1i$
Properties Of Subtraction Of Complex Numbers
| Name of the Property | Description | Expression |
| Closure property | Deduction of any two complex numbers gives the complex number | $z_1-z_2=z$
|
| Commutative property | The deduction of complex numbers is not commutative. | - |
| Associative property | The deduction of complex numbers is not associative. | - |
Multiplication Of Complex Numbers(*)
Multiplying any two complex numbers is equal to the multiplication of two binomials.
Let us assume that Z1= a + bi and z2= c + di.
On multiplying we obtain:-
$\lgroup\:a + bi\rgroup ∗ \lgroup\:c + di\rgroup = \lgroup\:a + bi\rgroup ∗ c + \lgroup\:a + bi\rgroup ∗ di$
$\lgroup\:a + bi\rgroup ∗ \lgroup\:c + di\rgroup = \lgroup\:a ∗ c +\lgroup\:b ∗ c\:\rgroup\:i\:\rgroup+\lgroup\:\lgroup\:a ∗ d\rgroup\:i + b ∗ d ∗ −1\rgroup$
$\lgroup\:a + bi\rgroup ∗ \lgroup\:c + di\rgroup = \lgroup\:a ∗ c − b ∗ d + \lgroup\:[b ∗ c + a ∗ d\rgroup\rgroup$
Examples:-
$2i ∗ \lgroup2 + 6i\rgroup$
can be viewed as $\lgroup0 + 2i\rgroup ∗ \lgroup2 + 6i\rgroup$
$= 2i ∗ \lgroup2 + 6i\rgroup$
$= 2i + 18i^{2}$
$=2i-18$
$=-18+2i$
Properties Of Multiplication Of Complex Numbers
| Name of the Property | Description | Expression |
| Closure property | The product of any two complex numbers is always a complex number only | $z_1*z_2=z$
|
| Commutative property | Change of any order of any complex numbers does not change the result of their product (L.H.S=R.H.S) | $z_1*z_2=z_2*z_1$
|
| Associative property | Regrouping of any complex numbers does not change the result of their product (L.H.S=R.H.S) | $z_1*\lgroup\:z_2*z_3\rgroup=\lgroup\:z_1*z_2\rgroup*z_3$
|
| Distributive property | Multiplying any complex number with the sum of two complex numbers is given by: | $z_1*\lgroup\:z_2+z_3\rgroup=z_1*z_2+z_1*z_3$
|
Division Of Complex Numbers (/)
Let us assume any complex number
$z_1=c_1+id_1$
and $z_2=c_2+id_2$
then the quotient of $\frac{z_1}{z_2}$ is equal to,
$\frac{z_1}{z_2}=z_1*\frac{1}{z_2}$
Thus, to find $\frac{z_1}{z_2}$
we have to multiply z1 with the inverse of z2.
Properties of Division of Complex Numbers
| Name of the Property | Description |
| Closure property | The division of any complex numbers is not closure. |
| Commutative property | The division of any complex numbers is not commutative. |
| Associative property | The division of any complex numbers is not associative. |
In Mathematics, algebraic operations on complex numbers are given by four basic arithmetic operations which include addition, subtraction, multiplication, and division. The algebraic operations on complex numbers are defined purely by the algebraic methods. Some basic algebraic laws like associative, commutative, and distributive laws are used to explain the relationship between the number of operations. Since algebra is a concept based on known and unknown values (variables), its own rules are created to solve the problems.
In this article, we will cover the concept of the algebraic operation of complex numbers. This concept falls under the broader category of complex numbers. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of twelve questions have been asked on this concept, including one in 2013, one in 2016, one in 2017, one in 2019, two in 2020, three in 2021, and three in 2023.
Complex Numbers
The number which has no real meaning then these numbers are represented in complex forms. The general form of complex numbers are 
![]() where i is iota or
where i is iota or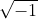
![]() .
.
A number of the form a + ib is called a complex number (where a and b are real numbers and i is iota). We usually denote a complex number by the letter z, z1, z2, etc
For example, z = 5 + 2i is a complex number.
5 here is called the real part and is denoted by Re(z), and 2 is called the imaginary part and is denoted by Im(z)
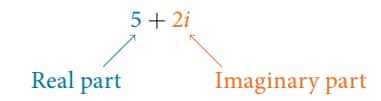
![]()
We will learn about addition, subtraction, multiplication, and division of complex numbers.
1. Addition of Two Complex Numbers
$z_1=a+i b$ and $z_2=c+i d$ be any two complex numbers. Then, the sum $z_1+z_2$ is defined as
$$
z_1+z_2=(a+i b)+(c+i d)=(a+c)+i(b+d)
$$
For example, $z_1=(3-4 i)$ and $z_2=(2+5 i)$, then $z_1+z_2$ is
$$
(3-4 i)+(2+5 i)=(3+2)+(-4+5) i=5+i
$$
2. Difference of Two Complex Numbers
$\mathrm{z}_1=\mathrm{a}+\mathrm{ib}$ and $\mathrm{z}_2=\mathrm{c}+\mathrm{id}$ be any two complex numbers. Then, the difference $\mathrm{z}_1-\mathrm{z}_2$ is defined as
$$
z_1-z_2=(a+i b)-(c+i d)=(a-c)+i(b-d)
$$
For example, $z_1=(-5+7 i)$ and $z_2=(-11+2 i)$, then $z_1-z_2$ is
$$
\begin{aligned}
(-5+7 i)-(-11+2 i) & =-5+7 i+11-2 i \\
& =-5+11+7 i-2 i \\
& =(-5+11)+(7-2) i \\
& =6+5 i
\end{aligned}
$$
3. Multiplication of Two Complex Numbers
$z_1=a+i b$ and $z_2=c+i d$ be any two complex numbers. Then, the multiplication $z_1 \cdot z_2$ is defined as
$$
\begin{aligned}
z_1 \cdot z_2 & =(a+i b) \cdot(c+i d) \\
& =a c+i a d+i b c+i^2 b d \\
& =a c+i(a d+b c)-b d \\
& =(a c-b d)+i(a d+b c)
\end{aligned}
$$
For example, $z_1=(4+3 i)$ and $z_2=(2-5 i)$, then $z_1 \cdot z_2$ is
$$
\begin{aligned}
(4+3 i)(2-5 i) & =4(2)-4(5 i)+3 i(2)-(3 i)(5 i) \\
& =8-20 i+6 i-15\left(i^2\right) \\
& =(8+15)+(-20+6) i \\
& =23-14 i
\end{aligned}
$$
4. Division of Two Complex Numbers
$z_1=a+i b$ and $z_2=c+i d$ (and $z_2$ is non-zero) be any two complex numbers. Then, the division $\frac{z_1}{z_2}$ is defined as
![\\\mathrm{\frac{z_1}{z_2}=\frac{a+ib}{c+id}\cdot \frac{c-id}{c-id}}\\\mathrm{[multiplying \;numerator\;and\;denominator\;by\;c-id\;where\;one\;of\;c\;and\;d\;is\;non-zero]}\\\mathrm{\frac{z_1}{z_2}=\frac{ac-iad+ibc-i^2bd}{c^2-\left(id\right)^2}=\frac{ac+i\left(bc-ad\right)+bd}{c^2-i^2d^2}}\\\mathrm{\frac{z_1}{z_2}=\frac{ac+bd+i\left(bc-ad\right)}{c^2+d^2}}\\\mathrm{\mathbf{\frac{z_1}{z_2}=\frac{ac+bd}{c^2+d^2}+i\frac{bc-ad}{c^2+d^2}}}](https://cache.careers360.mobi/media/articles/uploads/froala_editor/images/2024/9/23/1727127351822.png)
![]()
Here, some properties are given that are frequently used in the algebraic operation of real numbers as well as complex numbers.
1. Closure law: The sum of two complex numbers is a complex number, i.e. $z_1+z_2$ is a complex number for all complex numbers $z_1$ and $z_2$.
2. Commutative law : for any two complex numbers $z_1$ and $z_2, z_1+z_2=z_2+z_1$
3. Associative law : for any three complex numbers $z_1, z_2$ and $z_3,\left(z_1+z_2\right)+z_3=z_1+\left(z_2+z_3\right)$
4. Additive identity: if the sum of a complex number $z_1$ with another complex number $z_2$ is $z_1$, then $z_2$ is called the additive identity. We have $z+0=z=0+z$, so 0 is the additive identity.
5. Additive inverse: To every complex number $z=a+i b$, we have the complex number $-a+i(-b)$ (denoted as $-z)$, called the additive inverse or negative of $z$. $i . e . ~ z+(-z)=0(-z$ is additive inverse).
Summary
We concluded that the algebraic operation is an important aspect of complex numbers. It helps in the analysis of two or more than two complex numbers at the same time. Algebraic operations provide a detailed view of complex numbers and their significance. Different types of algebraic operations like addition, subtraction, multiplication, division exit for simplifying complex numbers
Recommended Video :
Solved Examples Based Algebraic Operations on Complex Numbers:
Example 1: Let 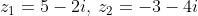
![]() then
then 
![]() equals:
equals:
Solution:
As we learned in
Subtraction of Complex Numbers -
=$\begin{aligned} & (\mathrm{a}+\mathrm{ib})-(\mathrm{c}+\mathrm{id})=(\mathrm{a}-\mathrm{c})+\mathrm{i}(\mathrm{b}-\mathrm{d}) \\ & z_1-z_2=(5-2 i)(-3-4 i)=(5-(-3))+(-2-(-4)) i=8+2 i \\ & \therefore z_1-z_2=8+2 i\end{aligned}$
Hence, the answer is 8+2i.
Example 2: Let 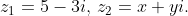
![]() If
If 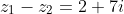
![]() then
then 
![]() equals
equals 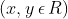
![]() :
:
Solution:
As we learned in
Subtraction of Complex Numbers -
$$
\begin{aligned}
& (\mathrm{a}+\mathrm{ib})-(\mathrm{c}+\mathrm{id})=(\mathrm{a}-\mathrm{c})+\mathrm{i}(\mathrm{b}-\mathrm{d}) \\
& z_1-z_2=(5-3 i)-(x+i y)=(5-x)+(-3-y) i
\end{aligned}
$$
But $z_1-z_2=2+7 i$
$\therefore$ Using the concept, we get
$5-x=2$ and $-3-y=7$
So, $x=3$ and $y=-10$
$$
\therefore x+y=-7
$$
Example 3: Let 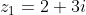
![]() and
and 
![]() then
then 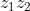
![]() equals
equals
Solution:
As we learned in
Multiplication of Complex Numbers -
$\begin{aligned} & (\mathrm{a}+\mathrm{ib})(\mathrm{c}+\mathrm{id})=(\mathrm{ac}-\mathrm{bd})+\mathrm{i}(\mathrm{bc}+\mathrm{ad}) \\ & z_1 z_2=(2+3 i)(-1-5 i)=\{(2)(-1)-(3)(-5)\}+i\{(3)(-1)+(2)(-5)\} \\ & \Rightarrow z_1 z_2=13-13 i\end{aligned}$
Example 4: What is the additive identity of the complex number 0?
1) Complex number
2) Natural number
3) Imaginary Number
4) None of these
Solution:
A number that can be expressed in a+ib form is called a complex number.
The additive identity of any complex number is 0+0i
real part=a=0, and Imaginary part= b= 0
it's given that $z=0=0+0 i$ and
$$
z+0=z=0+z
$$
Therefore, $(0+0 \mathrm{i})+(0+0 \mathrm{i})=0+0 \mathrm{i}$
Hence, the answer is the option 1.
Example 5: What is the additive inverse of 2 - 4i?
Solution:
Now,
Given complex number is 2 - 4i. a=2, b=-4
For a complex number z, the additive inverse is (-z).
so its additive inverse is -(2-4 i)=-2+-(-4) i=-2+4 i
Hence, the answer is -2+4i.
Frequently Asked Questions(FAQ)-
1. What do you understand by algebraic operations?
Ans: Algebraic operations mean that we do operations like addition, subtraction, multiplication, and division on more than one number.
2. What is additive inverse?
Ans: Additive inverse means that the number is multiplied by -1.
3. What type of number is the additive identity of the complex number 0?
Ans: Complex numbers
4. What do you understand by closure law?
Ans: Closure law signifies that the sum of two complex numbers is also a complex number.
5. What do you understand by the multiplication of two complex numbers?
Ans: Multiplication of complex numbers is a fundamental operation in complex arithmetic, which allows us to combine two complex numbers to produce another complex number.
Frequently Asked Questions (FAQs)
A complex number is any number that can be expressed in the form of a + bi, where a and b are real figures (a, b ∈ R), and i represents the imaginary unit, satisfying the equation i^{2}=-1 ![]()
No, it cannot be applied because the division of any complex numbers is not commutative.
There are four types of algebraic operations we basically use on complex numbers. They are
Addition
2. Subtraction
3. Multiplication
4. Division
Let us say that z1 and z2 are the two complex numbers
z_1=\lgroup\:a+ib\rgroup
![]()
z_2=\lgroup\:c+id\rgroup
![]()
In addition, these two complex numbers will be equal to
z_1+z_2=\lgroup\:a+ib\rgroup+\lgroup\:c+id\rgroup
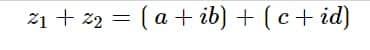
=\lgroup\:a+c\rgroup+i\lgroup\:b+d\rgroup
![]()
Which gives another complex number whose real part is Re( z1) + Re( z2) = a+ c and the imaginary part of the new complex number = Im( z1) + Im( z2) = b + d.
Example: \lgroup2+3i\rgroup+\lgroup2+2i\rgroup=\lgroup2+2\rgroup+\lgroup3+2\rgroup\:i=4+5i
Also Read
23 Sep'24 05:35 PM
23 Sep'24 05:34 PM
23 Sep'24 01:12 PM
23 Sep'24 01:11 PM
23 Sep'24 10:11 AM
23 Sep'24 10:05 AM
23 Sep'24 10:00 AM
23 Sep'24 09:59 AM
23 Sep'24 09:57 AM
23 Sep'24 09:55 AM
