Area of an Ellipse Proof for Area, Formula and Examples

Area Of Ellipse

Edited By Team Careers360 | Updated on Jul 02, 2025 05:27 PM IST

The amount of space included within an ellipse is referred to as its area. Alternatively, the total number of unit squares that can fit inside of an ellipse represents its area. The semi-major axis length, semi-minor axis length, and pi are used to calculate the ellipse's area. The area of an ellipse is equivalent to that of a circle. An ellipse's area is measured in square units.

This Story also Contains

What Is An Ellipse?
What Is The Area Of An Ellipse?
How To Calculate The Area Of An Ellipse?
Points To Remember
Why Calculate The Ellipse's Area?

What Is An Ellipse?

You may have noticed a variety of ellipse-shaped objects in your daily life, such as a cricket pitch, a badminton racket, a planet's orbit, etc. When a cone is sliced by an oblique plane in a way that produces a closed curve that does not bisect the base, an ellipse appears to be just like an ordinary oval shape. Ellipse is a 2-D object that is created by joining all the points on the plane that are always at the same distance from the two fixed points. The fixed endpoints are known as ellipse foci. Because an ellipse is not a perfect circle, there is a variation in the distance between its centre and its points on the circumference. An ellipse, therefore, has two radii. The major axis of the ellipse is the term used to describe the ellipse's longest chord. The chord that bisects the major axis perpendicularly is known as the minor axis.

What Is The Area Of An Ellipse?

The region that an ellipse covers in two dimensions is known as its area. Given the lengths of the main and minor axes, a general formula can be used to get the area of an ellipse. The following is the formula to determine an ellipse's surface area:

A=\pi ab

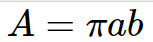
1707112911609

Here, ‘a’ represents the semi-major axis's length and ‘b’ represents the semi-minor axis's length.

Semi-major and Semi-minor axes are the names given to the halves of the Major and Minor axes, respectively.

How To Calculate The Area Of An Ellipse?

The lengths of the major and minor axes can be used to compute the area of an ellipse using the four steps below:

Step 1: Calculate the distance between the ellipse's centre and its farthest point, that is, the semi-major axis length.

Step 2: Calculate the separation between the nearest point on the ellipse and the centre, that is, the semi-minor axis length.

Step 3: Find the product of pi, a and b.

Step 4: Follow the area with square units.

Points To Remember

Ellipse is the collection of all points whose sum of the distances from two fixed points on a plane is constant.
Utilize the formula for the area of an ellipse after determining the semi-major axis (a) and semi-minor axis (b) values.
The formula for calculating the area of the ellipse is: A=\pi ab
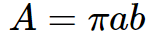
Consider the value of pi as 3.14 or 22/7.

Why Calculate The Ellipse's Area?

There are numerous numbers and fields that can be calculated using the area of an ellipse, including:

Calculating a large table's or an oval table top's volume.
Calculate the area of an oval building, such as a dome.
Building an elliptical pipe or a tunnel for agriculture.
To compare the airflow through round versus oval furnace holes.

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Frequently Asked Questions (FAQs)

1. What are the terms required to compute the area of an ellipse?

The semi-major axis length, semi-minor axis length, and pi are used to calculate the ellipse's area.

2. What is an ellipse?

Ellipse is a 2-D object that is created by joining all the points on the plane that are always at the same distance from the two fixed points.

3. Why does an ellipse have two radii?

Because an ellipse is not a perfect circle, there is a variation in the distance between its centre and its points on the circumference. An ellipse, therefore, has two radii.

4. Define the major axis and minor axis.

The major axis of the ellipse is the term used to describe the ellipse's longest chord. The chord that bisects the major axis perpendicularly is known as the minor axis.

5. What is the formula for calculating the area of an ellipse?

Given the lengths of the main and minor axes, a general formula can be used to get the area of an ellipse. The following is the formula to determine an ellipse's surface area:

A=\pi ab

Here, ‘a’ represents the semi-major axis's length and ‘b’ represents the semi-minor axis's length.

6. What is the formula for the area of an ellipse, and what do the variables represent?

The formula for the area of an ellipse is A = πab, where A is the area, π is pi (approximately 3.14159), a is the length of the semi-major axis, and b is the length of the semi-minor axis. The semi-major and semi-minor axes are half the length of the longest and shortest diameters of the ellipse, respectively.

7. How can the area of an ellipse be derived using calculus?

The area of an ellipse can be derived using definite integrals. By expressing the equation of an ellipse in terms of x and y, we can set up an integral that represents the area between the curve and the x-axis. Evaluating this integral over the appropriate limits gives us the formula πab.

8. Why does the area of an ellipse formula use π, similar to the area of a circle?

The use of π in the ellipse area formula reflects the ellipse's relationship to the circle. An ellipse can be thought of as a "stretched" or "compressed" circle. The π factor accounts for the curved nature of the ellipse, similar to how it represents the ratio of a circle's circumference to its diameter.

9. Can the area of an ellipse ever be negative?

No, the area of an ellipse cannot be negative. Area is always a positive quantity representing the amount of space enclosed by a shape. In the formula A = πab, π is always positive, and a and b are lengths, which are also always positive. Therefore, the product πab is always positive.

10. How does changing the length of one axis affect the area of an ellipse?

Increasing the length of either the semi-major (a) or semi-minor (b) axis will increase the area of the ellipse. The relationship is linear for each axis: doubling one axis while keeping the other constant will double the area. This is evident from the formula A = πab.

11. How is the area of an ellipse different from the area of a circle?

While both are closed curves, the area of an ellipse is always less than that of a circle with a diameter equal to the ellipse's major axis. This is because an ellipse is "squashed" compared to a circle. The formula for an ellipse's area (πab) includes both the semi-major (a) and semi-minor (b) axes, whereas a circle's area (πr²) only depends on its radius.

12. What is eccentricity, and how does it relate to the area of an ellipse?

Eccentricity (e) is a measure of how much an ellipse deviates from a perfect circle. It's defined as e = √(1 - b²/a²), where a and b are the semi-major and semi-minor axes. While eccentricity doesn't directly appear in the area formula, it affects the shape of the ellipse and thus indirectly influences its area.

13. Can an ellipse have the same area as a circle? If so, under what conditions?

Yes, an ellipse can have the same area as a circle. This occurs when the product of the ellipse's semi-major and semi-minor axes (ab) equals the square of the circle's radius (r²). In other words, when πab = πr², the areas are equal. However, the shapes will still be different unless the ellipse is actually a circle (a = b = r).

14. How is the area of an ellipse related to the areas of the inscribed and circumscribed circles?

The area of an ellipse is always between the areas of its inscribed and circumscribed circles. The inscribed circle has a radius equal to the semi-minor axis (b), while the circumscribed circle has a radius equal to the semi-major axis (a). The ellipse's area (πab) is the geometric mean of these two circular areas (πb² and πa²).

15. How does the area of an ellipse change if both axes are scaled by the same factor?

If both the semi-major (a) and semi-minor (b) axes are scaled by a factor k, the new area will be k² times the original area. This is because A = πab becomes A' = π(ka)(kb) = k²(πab) = k²A. For example, doubling both axes (k=2) will quadruple the area.

16. What is an ellipse and how does it relate to the concept of area?

An ellipse is a closed, two-dimensional curve that resembles a flattened circle. It's defined as the set of points on a plane such that the sum of the distances from two fixed points (called foci) is constant. The area of an ellipse is the space enclosed within this curve, which is important in various applications in mathematics, physics, and engineering.

17. How does the area of an ellipse change as it approaches a circle shape?

As an ellipse approaches a circle shape, its semi-major (a) and semi-minor (b) axes become more similar in length. When they are exactly equal (a = b), the ellipse becomes a circle. The area formula A = πab simplifies to A = πr², where r is the radius of the circle. The area tends to increase as the ellipse becomes more circular, assuming the longer axis remains constant.

18. What is the parametric form of an ellipse, and how does it relate to the area?

The parametric form of an ellipse is x = a cos(t) and y = b sin(t), where t is a parameter that ranges from 0 to 2π. While this form doesn't directly give the area, it's useful for understanding the ellipse's shape and can be used in an alternative derivation of the area formula through parametric integration.

19. What is the significance of the semi-major and semi-minor axes in calculating the area of an ellipse?

The semi-major (a) and semi-minor (b) axes are crucial in defining the shape and size of an ellipse. They represent half the length of the longest and shortest diameters of the ellipse, respectively. In the area formula A = πab, they directly determine the ellipse's size. The product ab represents a kind of "average radius" squared, analogous to r² in the circle area formula.

20. How does the area of an ellipse change if it's rotated in space?

The area of an ellipse remains constant regardless of its rotation in space. Rotation changes the ellipse's orientation but doesn't affect its fundamental shape or size. This invariance under rotation is an important property in many applications, such as image processing and computer graphics.

21. How is the area of an ellipse related to conic sections?

An ellipse is one of the conic sections, along with circles, parabolas, and hyperbolas. It's formed when a plane intersects a cone at an angle less than that of the cone's side. Understanding the area of an ellipse is crucial for studying conic sections and their properties.

22. How does the area of an ellipse relate to Kepler's laws of planetary motion?

Kepler's second law of planetary motion states that a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. This concept is directly related to the area of an ellipse because planetary orbits are elliptical. Understanding ellipse areas is crucial for calculating orbital periods and velocities in celestial mechanics.

23. What is the relationship between the perimeter and the area of an ellipse?

Unlike for a circle, there's no simple exact formula relating an ellipse's perimeter to its area. The perimeter of an ellipse involves elliptic integrals and is typically approximated. However, both the perimeter and area increase as the ellipse gets larger, and both depend on the lengths of the semi-major and semi-minor axes.

24. How does the area of an ellipse compare to the area of a rectangle that encloses it?

The area of an ellipse is always less than the area of the rectangle that exactly encloses it. If the rectangle has sides 2a and 2b (where a and b are the semi-major and semi-minor axes of the ellipse), its area is 4ab. The ellipse's area is πab, which is approximately 78.54% of the rectangle's area (since π/4 ≈ 0.7854).

25. What's the difference between the area of an ellipse and the area of an ellipsoid?

The area of an ellipse is a two-dimensional measure of the space enclosed by the elliptical curve. An ellipsoid, being a three-dimensional object, has a surface area and a volume instead. The formulas for these are more complex and involve all three axes of the ellipsoid.

26. Is there a way to express the area of an ellipse in terms of its eccentricity?

Yes, the area of an ellipse can be expressed in terms of its eccentricity (e) and semi-major axis (a): A = πa²√(1-e²). This form is derived from the standard area formula A = πab and the relationship between eccentricity and the axes: e² = 1 - (b²/a²). This representation can be useful when working with orbital mechanics or other applications where eccentricity is a key parameter.

27. How does the concept of integration relate to finding the area of an ellipse?

Integration is fundamental to deriving the area of an ellipse. The process involves setting up a definite integral that represents the area between the ellipse curve and the x-axis. By integrating the function of the upper half of the ellipse from -a to a (where a is the semi-major axis) and doubling the result, we obtain the total area. This application of calculus demonstrates the power of integration in solving geometric problems.

28. Can the area of an ellipse be approximated without using π?

While π is inherent in the exact formula for an ellipse's area, approximations can be made without explicitly using π. One such approximation is A ≈ 4ab(1 - (a-b)²/(a+b)²)/3. This formula, known as Ramanujan's approximation, is highly accurate for most ellipses and doesn't require direct use of π in calculations.

29. What's the relationship between the area of an ellipse and its focal points?

The focal points of an ellipse don't directly appear in its area formula, but they're related to the eccentricity, which does affect the area. As the focal points move closer together (decreasing eccentricity), the ellipse becomes more circular, and its area increases if the major axis remains constant. Conversely, as the focal points move apart, the ellipse becomes more elongated, and its area decreases if the major axis is fixed.

30. How does the concept of aspect ratio apply to the area of an ellipse?

The aspect ratio of an ellipse is the ratio of its semi-major axis to its semi-minor axis (a:b). While this ratio doesn't directly determine the area, it affects the shape of the ellipse. Ellipses with the same area can have different aspect ratios, resulting in different shapes. The aspect ratio is important in fields like optics and image processing where the shape of an ellipse matters as much as its area.

31. Can the area of an ellipse be expressed as a function of its circumference?

Unlike a circle, there's no simple exact relationship between an ellipse's area and its circumference. The circumference of an ellipse involves elliptic integrals and is usually approximated. However, some approximations relate area to circumference, such as A ≈ πC²/16, where C is the circumference. These are most accurate when the ellipse is close to circular.

32. How does the area of an ellipse relate to the concept of moments of inertia in physics?

The area of an ellipse is crucial in calculating its moment of inertia, which is important in rotational dynamics. For a flat elliptical disk rotating about its center, the moment of inertia is related to its mass and the lengths of its semi-major and semi-minor axes. Understanding the area is key to deriving these relationships in physics problems involving rotating elliptical objects.

33. What is the significance of the area of an ellipse in statistics and data visualization?

In statistics and data visualization, ellipses are often used to represent confidence regions in bivariate normal distributions. The area of these ellipses corresponds to the probability of data points falling within that region. Understanding ellipse areas is crucial for interpreting these visualizations and making statistical inferences about data distributions.

34. How does the concept of ellipse area apply in computer graphics and image processing?

In computer graphics and image processing, understanding ellipse areas is essential for tasks like shape recognition, object detection, and image segmentation. The area formula is used in algorithms that need to identify or manipulate elliptical shapes in images. It's also important in rendering and transforming elliptical objects in 2D and 3D graphics.

35. What is the relationship between the area of an ellipse and the golden ratio?

While there's no direct relationship between the area of an ellipse and the golden ratio (φ ≈ 1.618), ellipses with certain proportions can approximate the golden ratio. For instance, if the ratio of the semi-major axis to the semi-minor axis is φ, the resulting ellipse is sometimes called a "golden ellipse." This concept is more related to aesthetics and design than to the mathematical properties of area.

36. How does the area of an ellipse relate to the concept of eccentricity in astronomy?

In astronomy, the eccentricity of an elliptical orbit is related to its shape and, consequently, its area. Planets with more eccentric orbits (closer to 1) have more elongated elliptical paths, while those with eccentricities closer to 0 have more circular orbits. The area of the ellipse described by the orbit is important in calculations involving orbital periods and velocities, as described by Kepler's laws.

37. Can the area of an ellipse be used to solve real-world problems? Give an example.

Yes, the area of an ellipse has many practical applications. For example, in agriculture, crop circles are often elliptical rather than perfectly circular due to the angle of satellite imagery. Farmers and agricultural scientists use ellipse area calculations to estimate crop yields, plan irrigation systems, and manage resources more efficiently based on the actual planted area.

38. How does the concept of ellipse area apply in medical imaging?

In medical imaging, particularly in techniques like MRI and CT scans, ellipse area calculations are crucial. Organs and structures in the body are often approximated as ellipses in cross-sectional images. Doctors and radiologists use these area calculations to measure and track the size of organs, tumors, or other structures, helping in diagnosis and monitoring of various medical conditions.

39. What is the connection between the area of an ellipse and elliptic integrals?

While the area of an ellipse has a simple formula (πab), elliptic integrals come into play when dealing with more complex properties of ellipses, such as their perimeter. Elliptic integrals are a class of functions that naturally arise from attempting to determine the arc length of an ellipse. Understanding the area of an ellipse is often a stepping stone to working with these more advanced mathematical concepts.

40. How does the area of an ellipse relate to the concept of polar coordinates?

The area of an ellipse can be expressed and calculated using polar coordinates. In polar form, an ellipse is described by the equation r = ab/√((b cos θ)² + (a sin θ)²), where r is the radius and θ is the angle. Integrating r²/2 with respect to θ from 0 to 2π gives the area of the ellipse. This approach provides an alternative perspective on ellipse properties and can be useful in certain applications.

41. What is the significance of the area of an ellipse in optics and lens design?

In optics and lens design, the area of an ellipse is important in understanding and designing elliptical mirrors and lenses. Elliptical reflectors are used in various optical systems due to their focusing properties. The area of the elliptical cross-section of a lens or mirror affects its light-gathering power and focal properties, which are crucial in applications ranging from telescopes to microscopes.

42. How does the area of an ellipse relate to the concept of aspect ratio in display technologies?

In display technologies, the aspect ratio (width to height ratio) of screens is often described using values that relate to ellipse properties. For example, a 16:9 aspect ratio, common in modern widescreen displays, can be thought of as an ellipse with a semi-major to semi-minor axis ratio of 16:9. Understanding ellipse areas helps in calculating screen sizes, pixel densities, and image scaling in various display formats.

43. Can the area of an ellipse be used to approximate other shapes? How?

Yes, the area of an ellipse can be used to approximate other shapes, especially in computational geometry and image processing. For instance, complex or irregular shapes can often be approximated by fitting an ellipse that encloses or matches the shape as closely as possible. This "ellipse fitting" technique is used in computer vision, pattern recognition, and data analysis to simplify complex