Area of Quadrant - Formula, Definition, Examples
The locus of all points that are equally distant from the centre is referred to as a circle. Technically, a quadrant is one-fourth of a circle's section and is generated when a circle is evenly divided into four sections, or more accurately, four quadrants, by the intersection of two perpendicular lines. The space covered by one-fourth of a circle is referred to as the area of a quadrant, which is equal to one-fourth of the area of a circle. Half of a semicircle makes up the quadrant, and its area can be interpreted as the same as half of the semicircle's area. Each of a circle's four quadrants has an equal area, and the total area of the quadrants equals the area of the circle.
This Story also Contains
- What Is A Quadrant?
- How Is The Area Of A Quadrant Calculated?
- Steps To Find The Area Of A Quadrant
What Is A Quadrant?
Quadrants are the four quarters of the coordinate plane system. The term "quadrant" refers to each of the four sections. A quadrant, or a sector of 90 degrees, is the term used to describe the quarter of a circle. When four of these quadrants are combined, the only structure that results is a ‘circle’. Each of these quadrants has an equal area and size. Two perpendicular straight lines that represent the radius and an arc that represents one-fourth of a circle's circumference make up a quadrant.
How Is The Area Of A Quadrant Calculated?
We need to know the area of a circle in order to compute the area of a quadrant of a circle. We need to know the radius of a circle in order to calculate its area.
Area of circle (A) = \pi r^{2} 
Here, “r” is the radius of the circle.
Radius is described as the length of a line segment from the circle's centre to any point on its periphery. Now, divide a circle's area by four to determine the area of a quadrant (as four quadrants make a circle). We get,
Area of a quadrant = \frac{\pi r^{2}}{4}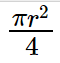 
Steps To Find The Area Of A Quadrant
It is simple to calculate the quadrant's area using its radius. Finding a circle's quadrant's area can be done by using the processes below:
Take a measurement of the quadrant's radius, which is the same as the corresponding circle's radius. In addition, the radius is the same as the circle's half-diameter.
From the circle’s radius, compute the area of the circle.
Calculate the quadrant's area, which is equal to one-fourth of the circle's area.
Apply the proper square units to the quadrant's area.
