Derangement: Concepts, Definition & Solved Examples

Derangement is a permutation of the elements of a set, such that no element appears in its original position. One of the common examples of derangement is as follows: There are n letters and corresponding envelopes. Then derangement means no letter is placed in its corresponding(correct) envelope. In real life, we use derangement in puzzles, crystallography, and probability.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Derangement: definition
2. Shortcut to solve derangement questions
3. Example of Derangement
4. Summary
5. Recommended Video :Solved Example Based on Derangement

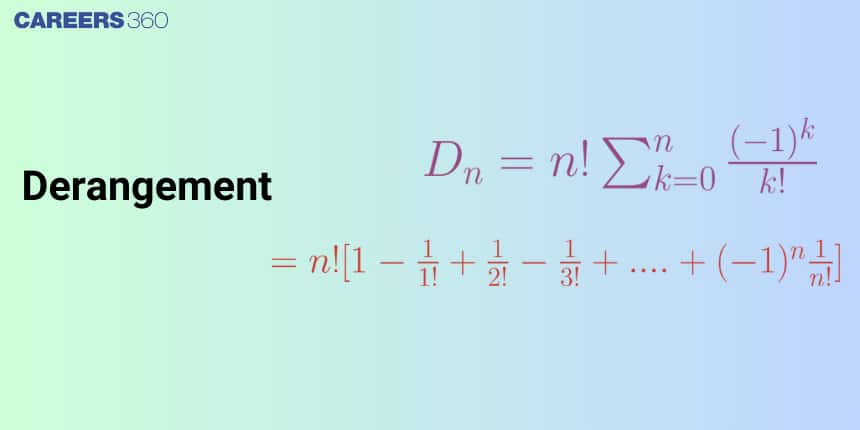
In this article, we will learn about the Derangement. This topic falls under the broader category of Permutations and combinations, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE.

Derangement: definition

Derangement is a permutation of the elements of a set, such that no element appears in its original position. In other words, we can say derangement is a permutation that has no fixed points. One of the common examples of derangement is as follows: There are n letters and corresponding envelopes. Then derangement means no letter is placed in its corresponding(correct) envelope.

Derangement: If there are n things and n places, one correct place corresponds to each object. Then an arrangement in which none of the objects is in its right place is called a derangement.

The number of ways of doing this is denoted by D(n) (the number of ways of deranging ‘n’ objects).

The formula for the derangement is given by

$\mathrm{D}(\mathrm{n})=\mathrm{n}!\left(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\ldots+(-1)^{\mathrm{n}} \frac{1}{\mathrm{n}!}\right)$

Shortcut to solve derangement questions

Substituting the value of ‘n’ as 1, 2, 3, 4, 5, 6 we will get,

D(1)= 0

D(2)= 1

D(3)= 2

D(4)= 9

D(5)= 44

D(6)= 265

A quicker way to find out the total number of possible derangements is just to memorize the above values by heart and use them instantly in the questions.

Example of Derangement

Example: In how many ways can you form a dancing couple from 3 boys and 3 girls so that no boy dances with his respective girlfriend?

Solution: This is clearly a case of derangement of 3 boys and 3 girls.

The value can be interpreted as D(3) =2 ways

Summary

Derangement represents a concept in combinatorial mathematics, where permutations are done under the constraint that no element occupies its original position. This restriction leads to unique counting challenges and finds applications in diverse fields ranging from cryptography to puzzles and probability theory. Knowledge of derangement helps us to solve and analyze problems related to real-life applications.

Recommended Video :
Solved Example Based on Derangement

Example 1: In an examination, 5 students have been allotted their seats as per their roll numbers. The number of ways, in which none of the students sits on the allotted seat, is ______: [JEE MAINS 2023]

Solution

$\mathrm{D}_5=5!\left(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\frac{1}{5!}\right)$

$\begin{aligned} \text { Derangement of 5 students } & =120\left(\frac{1}{2}-\frac{1}{6}+\frac{1}{24}-\frac{1}{120}\right) \\ & =60-20+5-1 \\ & =40+4 \\ & =44\end{aligned}$

Hence, the answer is 44.

Example 2: The number of ways in which a matrix match arrangement of order 55 with one-to-one correspondence can be attempted such that none of the parts is correctly matched is

Solution: We know that,

If n things are arranged in a row, the number of ways in which they can be arranged, so that none of them occupies its correct place is

$=n!\left(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}+\ldots+(-1)^n \frac{1}{n!}\right)$

Now,

Clearly, number of ways = D(5) = $5!\left(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\frac{1}{5!}\right)=60-20+5-1=44$

Hence, the answer is 44

Example 3: In how many ways can 10 letters be placed in 10 addressed envelopes such that exactly 9 letters are in the correct envelope?

Solution: If exactly 9 letters are in their correct envelopes, then the 10th will definitely be in its correct envelope as well

So, no such way

Hence, the answer is 0

Example 4: A person writes letters to five friends and addresses the corresponding envelopes. In how many ways can the letters be placed in the envelopes such that at least two of them are in the wrong envelope?

Solution: The standard formula for calculating D(n)

$
\mathrm{D}(\mathrm{n})=\mathrm{n}!\left(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\ldots+(-1)^{\mathrm{n}} \frac{1}{\mathrm{n}!}\right)
$
Also, $D(1)=0, D(2)=1, D(3)=2, D(4)=9, D(5)=44, D(6)=265$
Now,

$
\begin{array}{lllll}
\mathrm{L}_1 & \mathrm{~L}_2 & \mathrm{~L}_3 & \mathrm{~L}_4 & \mathrm{~L}_5 \\
& & & & \\
\mathrm{E}_1 & \mathrm{E}_2 & \mathrm{E}_3 & \mathrm{E}_4 & \mathrm{E}_5
\end{array}
$

The total number of ways of putting 5 letters into 5 envelopes is 5!

The number of ways to place all letters to correct envelopes is 1

Number of ways to place 1 letter in the wrong envelope and the other 4 into the correct envelope = 0

Hence, the number of ways in which at least two letters go into the wrong envelopes

= Total ways - ways to put 0 letters in the wrong place - ways to put one letter in the wrong place

= 5! - 1 - 0

= 119

Hence, the answer is 119

Example 5: The number of arrangements of all digits of 12345 such that at least 3 digits will not come in its position is:

Solution: Total number of ways such that at least 3 digits will not come in its position.

=Derangement of 3 digits +Derangement of 4 digits +Derangement of 5 digits

$\begin{aligned}= & { }^5 \mathrm{C}_3\left\{3!-{ }^3 \mathrm{C}_1 2!+{ }^3 \mathrm{C}_2 1!-{ }^3 \mathrm{C}_3 0!\right\} \\ + & +{ }^5 \mathrm{C}_4\left[4!-{ }^4 \mathrm{C}_1(3!)+{ }^4 \mathrm{C}_2(2!)-{ }^4 \mathrm{C}_3(1!)+{ }^4 \mathrm{C}_4(0!)\right\} \\ & +{ }^5 \mathrm{C}_5\left\{5!-{ }^5 \mathrm{C}_1 4!+{ }^5 \mathrm{C}_2 3!-{ }^5 \mathrm{C}_3 2!+{ }^5 \mathrm{C}_4 1!-{ }^5 \mathrm{C}_5(0!)\right\} \\ = & 10(2)+5(9)+(44) \\ = & 20+45+44=109\end{aligned}$

Hence, the answer is 109