Derivative of a Function wrt Another Function

Differentiation of a function with respect to another function is one of the important parts of Calculus, which helps to analyze the properties of the function with respect to another function. Mathematically, it forms a powerful tool by which slopes of functions are determined, the maximum and minimum of functions found, and problems on motion, growth, and decay, to name a few. These concepts of differentiation have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Function
2. Derivative of a Function
3. Derivative of a function with respect to another function
4. Solved Examples Based on Derivative of a Function with respect to Another Function
5. Summary

In this article, we will cover the concept of higher-order derivative of a Function. This concept falls under the broader category of Calculus, a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last five years of the JEE Main exam (from 2013 to 2023), a total of nine questions have been asked on this concept, including one in 2020, two in 2021, two in 2022, and four in 2023.

Function

$A$ and $B$ are two non-empty sets, then a relation from $A$ to $B$ is said to be a function if each element $x$ in $A$ is assigned a unique element $f(x)$ in $B$, and it is written as
$f: A \rightarrow B$ and read as $f$ is a mapping from $A$ to $B$.

Derivative of a Function

Let $f$ be defined on an open interval $I \subseteq$ containing the point $x_0$, and suppose that $\lim _{\Delta x \rightarrow 0} \frac{f\left(x_0+\Delta x\right)-f\left(x_0\right)}{\Delta x}$ exists. Then $f$ is said to be differentiable at $x_0$ and the derivative of $f$ at $x_0$, denoted by $f^{\prime}\left(x_0\right)$, is given by

$
f^{\prime}\left(x_0\right)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_0+\Delta x\right)-f\left(x_0\right)}{\Delta x}
$

For all $x$ for which this limit exists,
$f^{\prime}(x)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}$ is a function of $x$.

In addition to $f^{\prime}(x)$, other notations are used to denote the derivative of $y=f(x)$. The most common notations are $f^{\prime}(x), \frac{d y}{d x}, y^{\prime}, \frac{d}{d x}[f(x)], D_x[y]$ or $D y$ or $y_1$. Here $\frac{d}{d x}$ or $D$ is the differential operator.

Properties of derivative of a function

1. The derivative of sum of two functions is equal to the sum of their derivatives.

(i.e)., $\frac{d}{dx}[f(x)+g(x)] = \frac{d}{dx}[f(x)]+\frac{d}{dx}[g(x)]$

2. The derivative of differnce betweeen two functions is equal to the difference between their derivatives.

(i.e)., $\frac{d}{dx}[f(x)+g(x)] = \frac{d}{dx}[f(x)]+\frac{d}{dx}[g(x)]$

3. The derivative of the product of two functions is given by

$\frac{d}{dx}[f(x)g(x)] = (\frac{d}{dx}f(x))g(x)+f(x)(\frac{d}{dx}g(x))$

4. The derivative of the quotient of two functions is given by

$\frac{d}{dx}[\frac{f(x)}{g(x)}] = \frac{(\frac{d}{dx}f(x))g(x)+f(x)(\frac{d}{dx}g(x))}{(g(x))^2}$

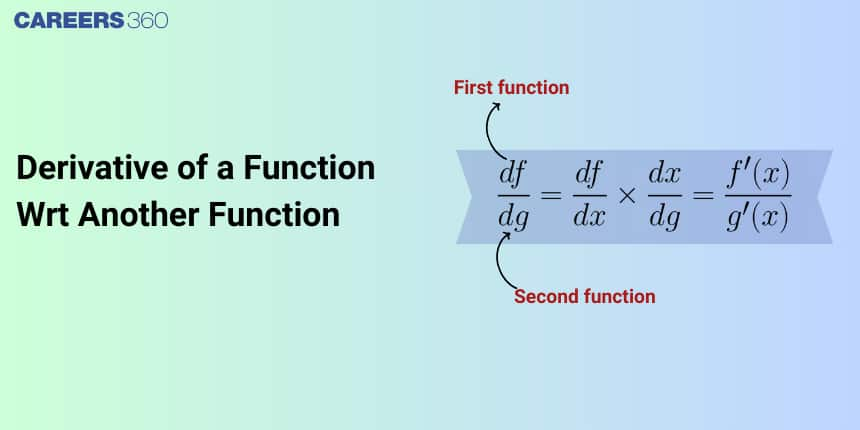
Derivative of a function with respect to another function

Derivative of a function with respect to another function is differentiating two functions with a dependent vaiable. toChain rule can be usedo find the derivative of a function with respect to another.

Chain rule

Let $f(x)$ and $g(x)$ be two functions. To differentiate $f(x)$ with respect to $g(x)$, Let $u=f(x)$ and $v=g(x)$.

$\left(\frac{\mathrm{d} u}{\mathrm{~d} v}\right)=\frac{\frac{\mathrm{d} u}{\mathrm{~d} x}}{\frac{\mathrm{d} x}{\mathrm{~d} v}}$ where $\frac{\mathrm{d} x}{\mathrm{~d} v}\neq0$

Recommended Video Based on Derivative of a Function with respect to Another Function

Solved Examples Based on Derivative of a Function with respect to Another Function

Example 1:Find the second order derivative if x and y are given by $x=a \sin t$ and $y=a \operatorname{cost}$
1) $
\frac{1}{a} \cos ^3 t
$

2) $
-\frac{1}{a} \cos ^3 t
$

3) $
\frac{1}{a} \sec ^3 t
$

4) $
-\frac{1}{a} \sec ^3 t
$

Solution:

Differentiating the function implicitly with respect to " $x$ ";

$
\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{\frac{d y}{d t}}{\frac{\mathrm{~d} x}{d t}}=\frac{-a \sin t}{a \cos t}=-\frac{\sin t}{\cos t}
$

Again differentiating with respect to " $x$ ";

$
\begin{aligned}
& \frac{d^2 y}{d x^2}=\frac{\mathrm{d}}{\mathrm{~d} x}\left(\frac{d y}{d x}\right)=\frac{\mathrm{d}}{\mathrm{~d} t}\left(-\frac{\sin t}{\cos t}\right) \frac{d t}{d x} \\
& \frac{d^2 y}{d x^2}=-\left(\sec ^2 t\right) \times \frac{1}{a \cos t}=-\frac{\sec ^2 t}{a \cos t}=-\frac{1}{a} \sec ^3 t
\end{aligned}
$

Hence, the answer is the option 4.

Example 2: Differentiate $\cos \left(a x^2+b x+c\right)$ with respect to $sin$ $\left(l x^2+m x+n\right)$
1) $
\frac{-(2 a x+b) \cos \left(a x^2+b x+c\right)}{(2 l x+m) \sin \left(l x^2+m x+n\right)}
$

2) $
\frac{-(2 a x+b) \sin \left(a x^2+b x+c\right)}{(2 l x+m) \cos \left(l x^2+m x+n\right)}
$

3) $
\frac{-(2 l x+m) \cos \left(l x^2+m x+n\right)}{(2 a x+b) \sin \left(a x^2+b x+c\right)}
$

4) $
\frac{-(2 l x+m) \sin \left(l x^2+m x+n\right)}{(2 a x+b) \cos \left(a x^2+b x+c\right)}
$

Solution:

Let $f(x)=\cos \left(a x^2+b x+c\right)$ and $g(x)=\sin \left(l x^2+m x+n\right)$

$
\begin{aligned}
& \frac{d f}{d g}=\frac{f^{\prime}(x)}{g^{\prime}(x)} \\
& f^{\prime}(x)=-\sin \left(a x^2+b x+c\right)(2 a x+b) \\
& g^{\prime}(x)=\cos \left(l x^2+m x+n\right)(2 l x+m) \\
& \frac{f^{\prime}(x)}{g^{\prime}(x)}=\frac{-(2 a x+b) \sin \left(a x^2+b x+c\right)}{(2 l x+m) \cos \left(l x^2+m x+n\right)}
\end{aligned}
$

Hence, the answer is the option 2.

Example 3: Find the derivative of $\log _{10}(x)$ with respect to $x^3$.
1) $
\frac{1}{2 x^2\left(\log _e 10\right)}
$

2) $
\frac{1}{2 x^3\left(\log _e 10\right)}
$

3) $
\frac{1}{3 x^3\left(\log _e 10\right)}
$

4) $
\frac{1}{3 x^2\left(\log _e 10\right)}
$

Solution:

Let $u =\log _{10}(x)$ and $v=x^3$
Also,$\frac{d u}{d x}=\frac{1}{x \log _e(10)}$ and $\frac{d v}{d x}=3 x^2$
$\frac{d u}{d v}=\frac{\frac{d u}{d x}}{\frac{d v}{d x}}$
$= \frac{\frac{1}{x \log _c(10)}}{3 x^2}=\frac{1}{3 x^3 \log _e(10)}$

Hence, the answer is the option 3.

Example 4: If $y=\frac{\sqrt{\left(1+t^2\right)}-\sqrt{\left(1-t^2\right)}}{\sqrt{\left(1+t^2\right)}+\sqrt{\left(1-t^2\right)}}$ and $x=\sqrt{\left(1-t^4\right)}$ then $\frac{d y}{d x}$ is equal to
1) $
\frac{-1}{t^2\left\{1+\sqrt{\left.\left(1-t^4\right)\right\}}\right.}
$

2) $
\frac{\left\{\sqrt{\left(1-t^4\right)}-1\right\}}{t^6}
$

3) $
\frac{1}{t^2\left\{1+\sqrt{\left.\left(1-t^4\right)\right\}}\right.}
$

4) $
\frac{1-\sqrt{\left(1-t^4\right)}}{t^6}
$

Solution:
$
\begin{aligned}
& y=\frac{\left(\sqrt{1+t^2}-\sqrt{1-t^2}\right)^2}{\left(\sqrt{1+t^2}\right)^2-\left(\sqrt{1-t^2}\right)^2} \\
& =\frac{2-2 \sqrt{1-t^4}}{2 t^2}=\frac{1-\sqrt{1-t^4}}{t^2} \\
& \frac{d y}{d t}=\frac{t^2\left\{0-\frac{1}{2 \sqrt{1-t^4}} \times-4 t^3\right\}-\left\{1-\sqrt{1-t^4}\right\} 2 t}{t^4} \\
& =\frac{2 t^5}{\sqrt{1-t^4}}-2 t\left\{1-\sqrt{1-t^4}\right\} \\
& =\frac{2\left\{1-\sqrt{1-t^4}\right\}}{t^3 \sqrt{1-t^4}} \\
& \frac{d x}{d t}=\frac{-2 t^3}{\sqrt{1-t^4}} \\
& \frac{d y}{d x}=\frac{\sqrt{1-t^4}-1}{t^6}=\frac{-1}{t^2\left\{1+\sqrt{1-t^4}\right\}}
\end{aligned}
$

Hence, the answer is the option 1.

Example 5: If $y=x^3+e^x$, then find $\frac{d^2 y}{d x^2}$.
1) $
-\frac{\left(5 x+e^x\right)}{\left(3 x^2+e^x\right)^3}
$

2) $
-\frac{\left(6 x+e^x\right)}{\left(3 x^2+e^x\right)^3}
$

3) $
-\frac{\left(6 x+e^x\right)}{\left(3 x^2+e^x\right)^2}
$

4) $
-\frac{\left(5 x+e^x\right)}{\left(3 x^2+e^x\right)^2}
$

Solution:

Given that, $y=x^3+e^x$

$\begin{aligned} & \frac{d y}{d x}=3 x^2+e^x \\ & \Rightarrow \frac{d x}{d y}=\frac{1}{3 x^2+e^x} \\ & \Rightarrow \frac{d^2 x}{d y^2}=-\frac{1}{\left(3 x^2+e^x\right)^2} \frac{d}{\mathrm{~d} y}\left(3 x^2+e^x\right) \\ & \Rightarrow \frac{d^2 x}{d y^2}=-\frac{1}{\left(3 x^2+e^x\right)^2}\left[6 x+e^x\right] \frac{d x}{d y} \\ & \Rightarrow \frac{d^2 x}{d y^2}=-\frac{6 x+e^x}{\left(3 x^2+e^x\right)^2} \times \frac{1}{\left(3 x^2+e^x\right)} \\ & \Rightarrow \frac{d^2 x}{d y^2}=-\frac{6 x+e^x}{\left(3 x^2+e^x\right)^3}\end{aligned}$

Hence, the answer is the option (2)

Summary

Derivative of a Function with respect to another Function is an important concept in Calculus. It provides a deep understanding of how the functions interact and change. It is very helpful in practical applications for physics, economics, etc. The chain rule is used to find the derivative of a function with respect to another.