Differential equations with variables separable

Before we learn the concept of the variable separable form of the differential equation, let's first understand what a differential equation is. A differential equation is an equation involving one or more terms and the derivatives of one dependent variable with respect to the other independent variable. Differential equations with separable variables are types of special classes of first-order differential equations that can be solved by separating the variables and integrating both sides independently. This method is very straightforward and widely used because it simplifies the process of finding the solution. Due to this, these types of differential equations are easily solved as compared to other types of differential equations. It also helps in solving real-life problems like calculating the population growth of the country and finding radioactive decay.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What is a Differential Equation?
2. Separable Differential Equation
3. Variable Separable Differential Equation Definition
4. Solved Examples Based On Variable Separable Differential Equations
5. Summary

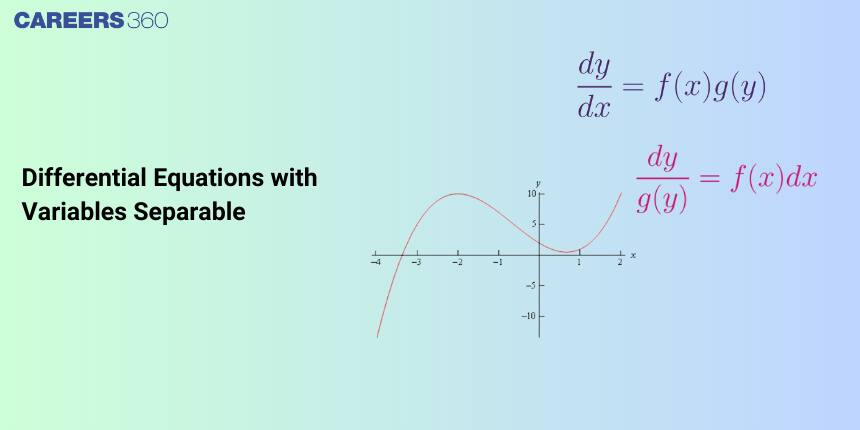
In this article, we will cover the concept of differential equations with variable separable methods. This concept falls under the broader category of differential equations, which is a crucial chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of nineteen questions have been asked on this concept, including one in 2015, one in 2017, one in 2019, five in 2020, six in 2021, four in 2022, and one in 2023.

What is a Differential Equation?

A differential equation is an equation involving one or more terms and the derivatives of one dependent variable with respect to the other independent variable.

Differential equation: dy/dx = f(x)

Where “x” is an independent variable and “y” is a dependent variable

Example of differential equation: $x \frac{d y}{d x}+2 y=0$
The above-written equation involves variables as well as the derivative of the dependent variable $\mathrm{y}$ with respect to the independent variable $\mathrm{x}$. Therefore, it is a differential equation.
The following relations are some of the examples of differential equations:
(i) $\frac{d y}{d x}=\sin 2 x+\cos x$
(ii) $\mathrm{k} \frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}=\left[1+\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^2\right]^{3 / 2}$

Separable Differential Equation

Differential equations where the variables can be separated from each other are called separable differential equations. The general form of a separable differential equation is dy/dx = f(x)g(y).

These equations can be easily solved by separating the variables and integrating them individually.

Variable Separable Differential Equation Definition

The differential of the form $\frac{d y}{d x}=f(x) g(y)$ where $f(x)$ is a function of $x$ and $g(y)$ is a function of $y$, are said to be variable separable form.

Steps to Solve differential equations using variable separable methods-

1. Check for any values of y that make g(y)=0. These correspond to constant solutions.
2. Rewrite the differential equation in the form $\frac{d y}{g(y)}=f(x) d x$
3. Integrate both sides of the equation.
4. Solve the resulting equation for y if possible.
5. If an initial condition exists, substitute the appropriate values for x and y into the equation and solve for the constant.

Rewrite the equation as
$
\frac{d y}{g(y)}=f(x) d x \quad[\text { where } g(y) \neq 0]
$

This process is separating the variables. Now, integrating both sides, we get
$
\int \frac{d y}{g(y)}=\int f(x) d x+c
$

By this, we get the solution of the differential equation

Let's see some illustration for a better understanding
(i) Solution of the differential equation $\frac{\mathrm{dy}}{\mathrm{dx}}=\left(\mathrm{e}^{\mathrm{x}}+1\right)\left(\mathrm{y}^2+1\right)$

Rewrite the differential equation as
$
\frac{\mathrm{dy}}{1+\mathrm{y}^2}=\left(\mathrm{e}^{\mathrm{x}}+1\right) \mathrm{dx}
$

Integrating both sides, we get
$
\begin{aligned}
& \int \frac{\mathrm{dy}}{1+\mathrm{y}^2}=\int\left(\mathrm{e}^{\mathrm{x}}+1\right) \mathrm{dx} \\
& \Rightarrow \tan ^{-1} y=e^x+x+c \\
& \Rightarrow y=\tan \left(e^x+x+c\right)
\end{aligned}
$

(ii) A differential equation of the form $\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{f}(\mathrm{ax}+\mathrm{by}+\mathrm{c})$ where $\mathrm{a}, \mathrm{b}$, and $\mathrm{c}$ are constants, can be converted into an equation with variables separable by the substitution $\mathrm{v}=\mathrm{ax}+\mathrm{by}+\mathrm{c}$.
$
\begin{aligned}
& \frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{f}(\mathrm{ax}+\mathrm{by}+\mathrm{c}) \\
& \mathrm{v}=\mathrm{ax}+\mathrm{by}+\mathrm{c} \\
& \therefore \frac{d v}{d x}=a+b \frac{d y}{d x} \text { or, } \frac{d y}{d x}=\frac{\frac{d v}{d x}-a}{b} \\
& \Rightarrow \frac{\frac{\mathrm{d} v}{\mathrm{dx}}-\mathrm{a}}{\mathrm{b}}=\mathrm{f}(\mathrm{v}) \Rightarrow \frac{\mathrm{dv}}{\mathrm{dx}}=\mathrm{bf}(\mathrm{v})+\mathrm{a} \\
& \Rightarrow \frac{\mathrm{dv}}{\mathrm{bf}(\mathrm{v})+\mathrm{a}}=\mathrm{dx}
\end{aligned}
$

In the differential equation (ii), the variables $\mathrm{x}$ and $\mathrm{v}$ are separated.
Integrating (ii), we get
$
\begin{aligned}
& \Rightarrow \quad \int \frac{d v}{b f(v)+a}=\int d x+C \\
& \Rightarrow \quad \int \frac{d v}{b f(v)+a}=x+C \text {, where } v=a x+b y+c
\end{aligned}
$

This represents the general solution of the differential equation (i).

Recommended Video Based on Variable Separable Differential Equations

Solved Examples Based On Variable Separable Differential Equations

Example 1: Which of the following can be solved using the variable separation method?

(1) $\frac{d y}{d x}=1+x y$
(2) $\frac{d y}{d x}=x^2 y$
(3) $\frac{d y}{d x}=\sin (x+y)$
(4) $\frac{d y}{d x}=x^y$

Solution:
In options (1),(3), and (4), $\mathrm{x}$ and $\mathrm{y}$ cannot be completely separated to make quantity involving $\mathrm{x}$ with $\mathrm{dx}$ and quantity involving $y$ with dy. But it can be done in option (2) as:
$
\frac{d y}{d x}=x^2 y \Rightarrow \frac{d y}{y}=x^2 d x
$

Hence, the answer is the option (2).

Example 2: Which of the following doesn't represent variable separated form?
(1) $\sin x d x+\cos y d y=0$
(2) $\sin (x+y) d x+\cos y d y=0$
$\left(1+x^2\right) d x+\frac{1}{y} d y=0$
(4) $\sec ^2 x d x+\tan y d y=0$

Solution:
The differential equations in options (1), (3) and (4) are of variable separable form.
But in option (2), we have:
$
\sin (x+y) d x+\cos y d y=0
$

In this, variables cannot be separated as $\sin (\mathrm{x}+\mathrm{y})$ is a composite function.
Hence, the answer is the option (2).

Example 3: Given that the slope of the tangent to a curve $y=y(x)$ at any point $(x, y)$ is $\frac{2 y}{x^2}$. If the curve passes through the centre of the circle $x^2+y^2-2 x-2 y=0$, then its equation is:

Solution:
Given the slope of the tangent $=\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{2 y}{x^2}$.
$
\frac{\mathrm{d} y}{\mathrm{y}}=\frac{2 d x}{\mathrm{x}^2}
$

Integrate both sides.
$
\ln (y)=-\frac{2}{x}+C
$

It passes through the center of the circle $x^2+y^2-2 x-2 y=0$ i.e $(1,1)$
$
0=-2+C \Rightarrow C=2
$

Eq. of the curve is
$
\begin{aligned}
& x \cdot \ln |y|=-2+2 x \\
& x \cdot \ln |y|=2(x-1)
\end{aligned}
$

Hence, the answer is $x \log _e|y|=2(x-1)$

Example 4: The solution of the differential equation $x\left(y^2+y\right) d x+(x+1) d y=0$ is:
Solution:
$
x y(y+1) d x+(x+1) d y=0
$

Dividing throughout by $y(y+1)(x+1)$, we get:
$
\begin{aligned}
& \frac{x d x}{(x+1)}+\frac{d y}{y(y+1)}=0 \\
& \Rightarrow \int \frac{x d x}{(x+1)}+\int \frac{d y}{y(y+1)}=c \\
& \Rightarrow \int \frac{(x+1)-1}{(x+1)} d x+\int \frac{(1+y)-y}{y(y+1)} d y=c \\
& \Rightarrow \int\left(1-\frac{1}{(x+1)}\right) d x+\int\left(\frac{1}{y}-\frac{1}{y+1}\right) d y=c \\
& \Rightarrow x-\ln |x+1|+\ln |y|-\ln |y+1|=c \\
& \Rightarrow \ln \left|\frac{y}{(x+1)(y+1)}\right|=c-x \\
& \Rightarrow\left|\frac{y}{(x+1)(y+1)}\right|=e^{c-x} \\
& \Rightarrow\left|\frac{y}{(x+1)(y+1)}\right|=c \cdot e^{-x} \\
&
\end{aligned}
$

Hence, the answer is $\left|\frac{y}{(x+1)(y+1)}\right|=c \cdot e^{-x}$

Example 5: Let $y=f(x)$ be the solution of the differential equation $y(x+1) d x-x^2 d y=0, y(1)=e$. Then $x \rightarrow 0^{+} f(x)$ is equal to

Solution:
$
\begin{aligned}
& y(x+1) d x-x^2 d y=0, \quad y(1)=e \\
& \Rightarrow \frac{d y}{d x}=\frac{y(x+1)}{x^2} \\
& \Rightarrow \int \frac{d y}{y}=\int \frac{(x+1) d x}{x^2} \\
& \ell \text { ny }=\ell \mathrm{nx}-\frac{1}{x}+c \\
& \because y(1)=e \\
& \therefore 1=0-1+C \Rightarrow C=2
\end{aligned}
$

Now, $\ell \mathrm{ny}=\ell \mathrm{nx}-\frac{1}{\mathrm{x}}+2$
$
\begin{aligned}
& \Rightarrow \ell \ln \left(\frac{y}{x}\right)=2-\frac{1}{x} \\
& \Rightarrow \frac{y}{x}=e^{2-\frac{1}{x}} \\
& \Rightarrow y=x, e^{2-\frac{1}{x}}
\end{aligned}
$

So, $\lim _{x \rightarrow 0^{+}} y=\lim _{x \rightarrow 0^{+}} x e^{2-\frac{1}{x}}=0$
Hence, the answer is 0.

Summary

Variable Separable differential equations are a useful and accessible class of differential equations that can be equated in many real-life phenomena, such as population growth and radioactive decay. By separating the variables and integrating both sides independently, we can find solutions that describe how these systems evolve. This method is a fundamental tool in the analysis of dynamic systems in various fields, including mathematics, biology, chemistry, and physics.