Differential form of Binomial Coefficient

An expression with two terms is called the binomial expansion. In the case of higher degree expression, it is difficult to calculate it manually. In these cases, Binomial theorem can be used to calculate it. Binomial theorem is used for the expansion of a binomial expression with a higher degree. Binomial coefficients are the coefficients of the terms in the Binomial expansion. Binomial theorem is proved using the concept of mathematical induction. Apart from Mathematics, Binomial theorem is also used in statistical and financial data analysis.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

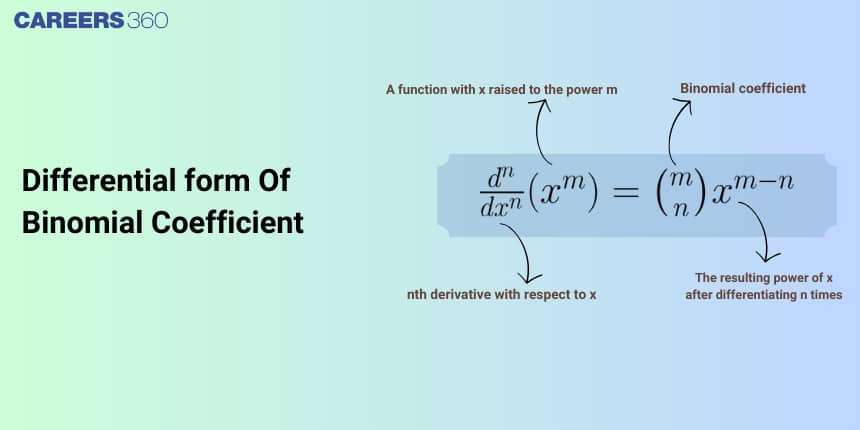
This article is about the differential form of the Binomial coefficients which falls under the broader category of Binomial Theorem and its applications. It is one of the important topics for competitive exams.

Binomial Theorem

If $n$ is any positive number, then $(a + b)^n = \binom{n}{0} a^n + \binom{n}{1} a^{n - 1} b + \binom{n}{2} a^{n - 2} b^2 + \dots + \binom{n}{n - 1} a b^{n - 1} + \binom{n}{n} b^n $

Binomial Coefficient

The combination $\binom{n}{r}$ or ${ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}$ occuring in the Binomial theorem is called a Binomial coefficient, where $\binom{n}{r}=C(n, r)={ }^n C_r=\frac{n!}{r!(n-r)!}$.

Differential Form of Binomial Coefficient

The differential form of binomial coefficient is $\frac{d}{d x}\binom{x}{k}=\binom{x}{k} \sum_{i=0}^{k-1} \frac{1}{x-i}$

Proof:

$\quad \frac{d}{d x}\left(\binom{x}{k}\right), \text { where }\binom{x}{k}=\frac{x!}{k!(x-k)!}=\frac{x(x-1)(x-2) \ldots 3.2 .1}{k!(x-k)(x-k-1)(x-k-2) \ldots 3.2 .1} $

$\text { Let y }=\frac{x(x-1)(x-2) \cdots(x-k+1)}{k!} $

$\ln (y)=\ln (x)+\ln (x-1)+\ln (x-2)+\cdots+\ln (x-k+1)-\ln (k!) $

$\frac{d y}{d x}\left(\ln (y)=\ln (x)+\ln (x-1)+\ln (x-2)+\cdots+\ln (x-k+1)-\ln (k!) \frac{1}{y} \cdot \frac{d y}{d x}=\right. $

$\frac{1}{x}+\frac{1}{x-1}+\frac{1}{x-2}+\cdots+\frac{1}{x-k+1}-0 $

$\frac{d y}{d x}=y \cdot\left(\frac{1}{x}+\frac{1}{x-1}+\frac{1}{x-2}+\cdots+\frac{1}{x-k+1}-0\right) $

$\frac{d y}{d x}=\binom{x}{k} \cdot \sum_{i=0}^{k-1} \frac{1}{x-i} $

$\frac{d}{d x}\binom{x}{k}=\binom{x}{k} \sum_{i=0}^{k-1} \frac{1}{x-i}

$

Summary

Binomial theorem is used for the expansion of a binomial expression with a higher degree. Binomial coefficients are the coefficients of the terms in the Binomial expansion. Understanding the differential form of the binomial coefficients gives an idea to solve more complex problems not only in mathematics but also in physics.

Recommended Video :

Solved Examples based on Differential Form of Binomial Coefficients

Example 1: The value of $\sum_{r=0}^n(r+1)^n C_r$ equals

1) $(n+2) 2^{n-1}$

2) $(n+1) 2^{n-1}$

3) $(n+2) 2^n$

4) $(n+4) 2^{n-1}$

Solution:

$C_1+2 \cdot C_2+3 \cdot C_3+---+n \cdot C_n=\sum_{r=0}^n r \cdot{ }^n C_r=n \cdot 2^{n-1}$

And

$C_0+C_1+C_2+C_3+---+C_n=2^n $

Now,

$\sum_{r=0}^n(r+1)^n C_r $

$= \sum_{r=0}^n\left(r .{ }^n C_r\right)+\sum_{r=0}^n\left({ }^n C_r\right) $

$\left({ }^n C_1+2^n C_2+\ldots .+n^n C_n\right)+\left({ }^n C_0+{ }^n C_1+\ldots .+{ }^n C_n\right) $

$\quad= n(2) 2^{n-1}+2^n $

$=(n+2) 2^{n-1} $

Example 2: Evaluate $\binom{4}{0}+2\binom{4}{1}+3\binom{4}{2}+4\binom{4}{3}+5\binom{4}{4}$

1) $40$

2) $36 $

3) $48 $

4) $64 $

Solution:

$C_1+2 \cdot C_2+3 \cdot C_3+---+n \cdot C_n=\sum_{r=0}^n r \cdot{ }^n C_r=n \cdot 2^{n-1} $

and

$ C_0+C_1+C_2+C_3+----+C_n=\sum_{r=0}^n\left({ }^n C_r\right)=2^n $

Now，

Given expression can be written as

$\sum_{r=0}^4(r+1)^4 C_r $

$=\sum_{r=0}^4(r) \cdot{ }^4 C_r+\sum_{r=0}^4\left({ }^4 C_r\right) $

$=4.2^3+2^4=32+16=48

Example 3: Find the value of $(1 \cdot 2) C_2+(2 \cdot 3) C_3+\ldots \ldots+\{(n-1) \cdot n\} C_n$.

If $\mathrm{C}_0, \mathrm{C}_1, \mathrm{C}_2, \ldots, \mathrm{C}_n$ be binomial coefficients in the expansion of $(1+x)^n$

1) $n(n+1) 2^{n-1}$

2) $n(n+1) 2^{n-2}$

3) $n(n-1) 2^{n-1}$

4) $n(n-1) 2^{n-2}$

Solution:

$ 1^2 \cdot C_1+2^2 \cdot C_2+3^2 \cdot C_3+---+n^2 \cdot C_n=\sum_{r=0}^n r^{2 \cdot n} C_r=n \cdot 2^{n-1}+n(n-1) 2^{n-2} $

Now,

Given expression can be written as

$\sum_{r=0}^n(r-1) r \cdot{ }^n C_r $

$= \sum_{r=0}^n r^2 \cdot{ }^n C_r-\sum_{r=0}^n r \cdot{ }^n C_r $

$= n \cdot 2^{n-1}+n(n-1) \cdot 2^{n-2}-n \cdot 2^{n-1} $

$= n(n-1) \cdot 2^{n-2} $

Hence, the answer is the option (4).

Example 4: The sum $\sum_{r=1}^{10}\left(r^2+1\right) \times(r!)$ is equal to:

1) (11)!

2) $10 \times(11!)$

3) $101 \times(10!)$

4) $11 \times(11!)$

Solution:

$\sum_{r=1}^{10}\left(r^2+1\right) \times(r!) $

$\Rightarrow \sum_{r=1}^{10}\left\{(r+1)^2-2 r\right\} r!$

$ \Rightarrow \sum_{r=1}^{10}\left\{(r+1)^2\right\} r!-2 \sum_{r=1}^{10} r \cdot r! $

$\Rightarrow \sum_{r=1}^{10}(r+1)(r+1) r!-2 \sum_{r=1}^{10} r \cdot r! $

$\Rightarrow \sum_{r=1}^{10}((r+1)(r+1)!-r \cdot r!)-\sum_{r=1}^{10} r \cdot r! $

$\Rightarrow(11.11!-1)-\sum_{r=1}^{10}((r+1)!-r!) $ \Rightarrow(11.11!-1-(11!-1!) $

$\Rightarrow 10.11!$

Example 5: Let $\mathrm{m}, \mathrm{n} \in N$ and n is odd and $30\binom{30}{0}+29\binom{30}{1}+\ldots \ldots+2\binom{30}{28}+1\binom{30}{29}=n .2^m$, then $n+m$ is equal to

1) $20 $

2) $65 $

3) $45 $

4) $75 $

Solution:

As we have learnt

$ \sum_{r=1}^n r\left({ }^n C_r\right)=n \cdot 2^{n-1} $

Now, given,

$ 30\binom{30}{0}+29\binom{30}{1}+\ldots+2\binom{30}{28}+1\binom{30}{29} $

this can be written as

$30\left({ }^{30} \mathrm{C}_0\right)+29\left({ }^{30} \mathrm{C}_1\right)+\ldots+2\left({ }^{30} \mathrm{C}_{28}\right)+1\left({ }^{30} \mathrm{C}_{29}\right) $

$=30\left({ }^{30} \mathrm{C}_{30}\right)+29\left({ }^{30} \mathrm{C}_{29}\right)+\ldots \ldots+2\left({ }^{30} \mathrm{C}_2\right)+1\left({ }^{30} \mathrm{C}_1\right) $

$=\sum_{r=1}^{30} r\left({ }^{30} C_r\right) $

$=30\left(2^{29}\right)=15(2)^{30}=\mathrm{n}(2)^{\mathrm{m}} $

$\therefore \mathrm{n}=15, \mathrm{~m}=30 $

$\mathrm{n}+\mathrm{m}=45 $