Distance Between Two Points Formula - Definition & Examples

For any two points, there is a unique line segment that connects them. The distance between two points is the length of the line segment joining the two points. The distance formula is used to calculate the distance between two points if their coordinates are given. It's important to remember that the distance is always a positive value.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What is the Distance Between Two Points?
2. Distance Between Two Points Formula
3. Derivation of Formula for Distance Between Two Points
4. Steps to Calculate Distance Between Two Points
5. Step 3: Express the given answer in units.
6. Solved Examples Based on the Distance Between Two Points

In this article, we will cover the concept of the Distance formula. This category falls under the broader category of Coordinate geometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. A total of five questions have been asked on JEE MAINS( 2013 to 2023) from this topic including four in 2019, and one in 2022

What is the Distance Between Two Points?

The distance between two points is the length of the line segment joining the two points. Distance between two points can be calculated by finding the length between two points. The distance formula is used to calculate the distance between two points if their coordinates are given.

Distance formula can be used to calculate the distance between two points if the points are on the plane or the points lie on the x-axis or y-axis.

Distance Between Two Points Formula

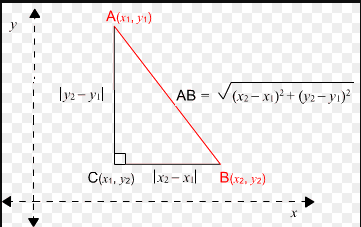
The distance formula is used to calculate the distance between two points if their coordinates are given. For any point given in the 2-D plane, we can apply the 2D distance formula or the Euclidean distance formula given as:

$|A B|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$

This is also known as the Euclidean Distance Formula.

Derivation of Formula for Distance Between Two Points

We can derive the distance formula by using Pythagoras' theorem.

Using Pythagoras Theorem

$\begin{aligned} & c^2=a^2+b^2 \\ & A B^2=a^2+b^2 \\ & A B^2=\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2 \\ & |A B|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\end{aligned}$

Important Points:

1) The distance of a point A (x, y) from the origin O (0, 0) is given by

$|O A|=\sqrt{(x-0)^2+(y-0)^2}=\sqrt{x^2+y^2}$

2) If the points lie on the x-axis, the Distance between (x₁,0) and(x₂,0) is |x₁-x₂|

3) If the points lie on the y-axis, the Distance between (y₁,0) and(y₂,0) is |y₁-y₂|

Steps to Calculate Distance Between Two Points

The distance between two points using the given coordinates can be calculated with the help of the following steps:

Step 1: Find the coordinates of the two points whose distance has to be calculated. Suppose, Point A (x₁, y₁) and B (x₂, y₂) are two points on the cartesian plane

Step 2: Use the distance formula to calculate the distance between two points. Distance between two points A, B = $|A B|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$

Step 3: Express the given answer in units.

Recommended Video Based on the Distance Between Two Points

Solved Examples Based on the Distance Between Two Points

Example 1: A rectangle $\text { R }$ with endpoints of one of its sides as $(1,2)$ and $(3,6)$ is inscribed in a circle. If the equation of the diameter of the circle is $2 x-y+4=0$, then the area of \text { R } is______________. [JEE MAINS 2022]

Solution: Let the center of the circle is $C(\alpha, 4+2 \alpha)$

It will be equidistant from $(1,2)(3,6)$

$
\begin{aligned}
& \Rightarrow(\alpha-1)^2+(4+2 \alpha-2)^2=(\alpha-3)^2+(4+2 \alpha-6)^2 \\
& \Rightarrow \alpha^2-2 \alpha+1+4 \alpha^2+8 \alpha+4=\alpha^2-6 \alpha+3+4 \alpha^2-8 \alpha+4 \\
& \Rightarrow 20 \alpha=8 \Rightarrow \alpha=\frac{4}{5} ; \quad \text { c: }\left(\frac{4}{5}, \frac{28}{5}\right) .
\end{aligned}
$
distance $\mathrm{b} / \mathrm{w}(1,2) \quad \&(3,6)=2 \sqrt{5}=$ length.

Equation of line joining $(1,2)$ and $(3,6)$ is
$
\begin{aligned}
& y-2=\frac{6-2}{3-1}(x-1) \\
& 2 x-y=0
\end{aligned}
$
distance of centre from $2 x-y=0$ is
$
\mathrm{d}=\frac{\left|2 \times \frac{4}{5}-\frac{28}{5}\right|}{\sqrt{2^2+1^2}}=\frac{4}{\sqrt{5}} \text { units }
$

So Breadth =$2 \times \frac{4}{\sqrt{5}}=\frac{8}{\sqrt{5}}$ units

$\text { Area of } \mathrm{R}=1 \times \mathrm{b}=2 \sqrt{5} \times \frac{8}{\sqrt{5}}=16 \text { sq.units. }$

So answer is $\text { 16sq.units. }$

Hence, the answer is 16.

Example 2: A number of the lines, among the lines 2 $\mathrm{x}+\mathrm{y}+4+\mathrm{k}(\mathrm{x}-2 \mathrm{y}-3)=0$; whose minimum distance is $\sqrt{10}$ from the point (2,-3) is:

Solution

We have $\left|\frac{(2+k) 2+(1-2 \mathrm{k})(-3)+4-3 \mathrm{k}}{\sqrt{(2+\mathrm{k})^2+(1-2 \mathrm{k})^2}}\right|=\sqrt{10}$
Simplifying this quadratic will yield an equal root $\mathrm{k}=1$

Hence, the answer is 1.

Example 3: The extremities of the base of an isosceles triangle are (2,0) and (0,2). If the equation of one of the equal sides is x=2, the equation of the other equal side is

Solution:

Let coordinates of isosceles triangle be A=(2,h),B=(2,0),C=(0,2)

so, AB=AC

By distance formula

$h^2=4+(h-2)^2$ $h^2=4+h^2+4-4 h$ $4 h=8$ $h=2$

Equation of line AC

y=2.
Hence, the answer is y=2.

Example 4: A triangle with vertices (4, 0), (–1, –1), (3, 5) is

Solution:

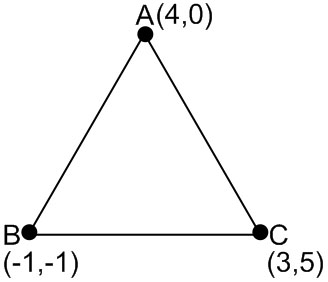
Using distance formula$\begin{aligned}
& A B=\sqrt{(4-(-1))^2+(0-(-1))^2}=\sqrt{25+1}=\sqrt{26} \\
& A C=\sqrt{(4-3)^2+(0-5)^2}=\sqrt{1+25}=\sqrt{26} \\
& B C=\sqrt{(3-(-1))^2+(5-(-1))^2}=\sqrt{16+36}=\sqrt{52}
\end{aligned}$

Clearly, AB = AC and $A B^2+A C^2=B C^2$

So, this is a right-angle isosceles triangle.

Example 5: Let A(h, k), B(1,1) and C(2,1) be the vertices of a right-angled triangle with A C as its hypotenuse. If the area of the triangle is 1 square unit, then the set of values which ' k^{\prime} can be taken is given by

Solution: The distance between the point $A\left(x_1, y_1\right)$ and $B\left(x_2, y_2\right)$ is $\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}$

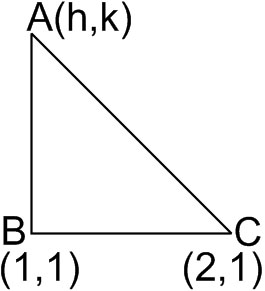
$\begin{aligned} & A C^2=A B^2+B C^2 \\ & (h-2)^2+(k-1)^2=(h+1)^2+(k-1)^2+1^2 \\ & 4-4 h=1-2 h+1 \\ & 2 h=2 \Rightarrow h=1\end{aligned}$

Also, $\frac{1}{2} A B \cdot B C=1$

$\begin{aligned} & \frac{1}{2} \times A B \times 1=1 \\ & A B=2=\sqrt{(h-1)^2+(k-1)^2} \\ & (k-1)^2=2^2 \\ & k-1=2 \quad \text { or } k=-1=-2\end{aligned}$

$k=3 \quad$ or $\quad k=-1$

Hence, the answer is {–1, 3}.

Summary

The distance formula is a concept used to calculate the distance between two points. We can also derive the distance formula with the help of Pythagoras' theorem. Distance formula has a wide variety of applications in mathematics and physics. Understanding the distance formula helps us in solving a variety of problems in real-life applications.