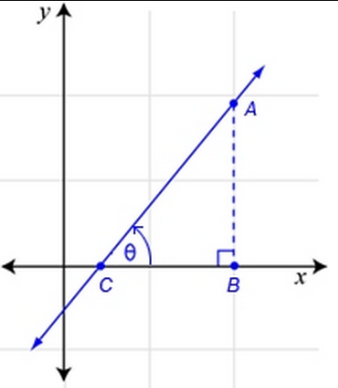
Equations of the Bisectors of the Angles between Two Straight Lines

An angle bisector is a line that evenly divides the angle between two intersecting lines into two equal angles. This bisector represents the locus of all points that are equidistant from both lines. In other words, an angle bisector maintains an equal perpendicular distance from each of the two intersecting lines.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Derivation of Equation of the Bisectors
2. Distinguish between obtuse and acute angle bisector
3. Solved Examples Based on Equation of the Bisectors
4. Summary

In this article, we will cover the concept of Equation of the Bisectors. This category falls under the broader category of Coordinate Geometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. A total of nineteen questions have been asked on JEE MAINS( 2013 to 2023) from this topic.

What is an Angle bisector?
The Locus of point which is equidistant from both lines is called the angle bisector. The bisector is the locus of a point that moves in the plane of lines $L_1$ and $L_2$ such that lengths of perpendiculars drawn from it to the two given lines( $L_1$ and $L_2$ ) are equal.

Equation of the Bisectors
The equation of the angle bisectors between the two lines
$
\begin{aligned}
& \mathrm{L}_1=\mathrm{a}_1 \mathrm{x}+\mathrm{b}_1 \mathrm{y}+\mathrm{c}_1=0 \text { and } \mathrm{L}_2=\mathrm{a}_2 \mathrm{x}+\mathrm{b}_2 \mathrm{y}+\mathrm{c}_2=0 \text { is } \\
& \frac{\left(\mathbf{a}_1 \mathbf{x}+\mathbf{b}_1 \mathbf{y}+\mathbf{c}_1\right)}{\sqrt{\mathbf{a}_1^2+\mathbf{b}_1^2}}= \pm \frac{\left(\mathbf{a}_2 \mathbf{x}+\mathbf{b}_2 \mathbf{y}+\mathbf{c}_2\right)}{\sqrt{\mathbf{a}_2^2+\mathbf{b}_2^2}}
\end{aligned}
$

Derivation of Equation of the Bisectors

Given equations of lines
$
\begin{aligned}
& L_1: A B: a_1 x+b_1 y+c_1=0 \\
& L_2: C D: a_2 x+b_2 y+c_2=0
\end{aligned}
$

RR' and SS' are two bisectors of the angle between the line $A B$ and $C D$. And, $P(x, y)$ be any point on the line RR', then length of perpendicular from P on AB
$
\begin{array}{ll}
& \text { = length of perepndicular from } \mathrm{P} \text { on } \mathrm{CD} \\
\therefore & \frac{\left|\mathrm{a}_1 \mathrm{x}+\mathrm{b}_1 \mathrm{y}+\mathrm{c}_1\right|}{\sqrt{\mathrm{a}_1^2+\mathrm{b}_1^2}}=\frac{\left|\mathrm{a}_2 \mathrm{x}+\mathrm{b}_2 \mathrm{y}+\mathrm{c}_2\right|}{\sqrt{\mathrm{a}_2^2+\mathrm{b}_2^2}} \\
\text { or } & \frac{\left(\mathrm{a}_1 \mathrm{x}+\mathrm{b}_1 \mathrm{y}+\mathrm{c}_1\right)}{\sqrt{\mathrm{a}_1^2+\mathrm{b}_1^2}}= \pm \frac{\left(\mathrm{a}_2 \mathrm{x}+\mathrm{b}_2 \mathrm{y}+\mathrm{c}_2\right)}{\sqrt{\mathrm{a}_2^2+\mathrm{b}_2^2}}
\end{array}
$

Bisector of the Angle Containing the Origin

Rewrite the equation of the line $a_1 x+b_1 y+c_1=0$ and $a_2 x+b_2 y+c_2=0$ such that the constant term $c_1$ and $c_2$ are positive.
Then, the equation
$
\frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{a_1^2+b_1^2}}=\frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{a_2^2+b_2^2}}
$
gives the equation of the bisector of the angle containing the origin and
$
\frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{a_1^2+b_1^2}}=-\frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{a_2^2+b_2^2}}
$
gives the equation of the bisector of the angle not containing the origin.

Distinguish between obtuse and acute angle bisector

Let, $\quad \mathrm{L}_1: \mathrm{a}_1 \mathrm{x}+\mathrm{b}_1 \mathrm{y}+\mathrm{c}_1=0$
$
\mathrm{L}_2: \mathrm{a}_2 \mathrm{x}+\mathrm{b}_2 \mathrm{y}+\mathrm{c}_2=0
$
where, $c_1>0, c_2>0$
Equation of bisectors are
$
\begin{aligned}
& \frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{a_1^2+b_1^2}}=\frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{a_2^2+b_2^2}} \\
& \frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{a_1^2+b_1^2}}=-\frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{a_2^2+b_2^2}}
\end{aligned}
$

To distinguish between acute angles and obtuse angle bisectors, choose one of the equations of bisector, say eq (iii). Let the angle between this bisector and one of the given lines be $/theta / 2$, where $\theta$ is an angle between lines containing these bisectors.

$
\begin{aligned}
& \theta<\pi / 2 \\
& \Rightarrow \quad \theta / 2<\pi / 4 \\
& \Rightarrow \quad|\tan (\theta / 2)|<1 \\
& \Rightarrow \quad \tan (\angle \mathrm{ROB})<1
\end{aligned}
$

Similarly, ROB is the bisector of an obtuse angle if, $|\tan (\theta / 2)|>1$

Shortcut Method for Identifying Acute Obtuse Angle Bisectors

The equation of two non-parallel lines are
$\mathrm{L}_1: A B: a_1 x+b_1 y+c_1=0$
$\mathrm{L}_2: \mathrm{CD}: \mathrm{a}_2 \mathrm{x}+\mathrm{b}_2 \mathrm{y}+\mathrm{c}_2=0$
Then equation of bisectors are
$
\frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{a_1^2+b_1^2}}= \pm \frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{a_2^2+b_2^2}}
$

Recommended Video Based on Equation of the Bisector

Solved Examples Based on Equation of the Bisectors

Example 1: The sides of a rhombus $A B C D$ are parallel to the lines, $x-y+2=0$ and $7 x-y+3=0$. If the diagonals of the rhombus intersect at $P(1,2)$ and the vertex $A$ (different from the origin) is on the $y$-axis, then the ordinate of $A$ is.

Solution: Let co-ordinate of $\mathrm{A}=(0, \mathrm{a})$
The equation of parallel lines are
$
x-y+2=0 \text { and } 7 x-y+3=0
$

Diagonals are parallel to angle bisectors, i.e.
$
\frac{x-y+2}{\sqrt{2}}= \pm\left(\frac{7 x-y+3}{5 \sqrt{2}}\right)
$
i.e. $L_1: 2 x+4 y-7=0$
$
\begin{aligned}
& L_2: 12 x-6 y+13=0 \\
& m_1=\frac{-1}{2} \text { and } m_2=2
\end{aligned}
$

Slope of $A(0, a)$ to $P(1,2)$ is
$
\frac{2-C}{1}=\frac{-1}{2} \Rightarrow C=\frac{5}{2}
$

Hence, the answer is $\frac{5}{2}$.

Example 2: If one of the lines of $m y^2+\left(1-m^2\right) x y-m x^2=0$ is a bisector of the angle between the lines $x y=0$, then $m$ is

Solution:

$\begin{aligned} & m y^2+(1-m)^2 x y-m x^2=0 \\ & y(m y+x)-m x(m y+x)=0 \\ & (y-m x)(m y+x)=0 \\ & x y=0 \quad \text { is } x=0 \text { and } y=0\end{aligned}$

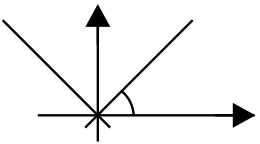
So the slope of the line equally inclined is:
$
\begin{aligned}
& \theta=\frac{\pi}{4} \\
& \tan \theta=1
\end{aligned}
$

Hence, the answer is 1.

Example 3: The perpendicular bisector of the line segment joining $P(1,4)$ and $Q(k, 3)$ has $y$-intercept -4. Then a possible positive value of $k$ is

Solution:

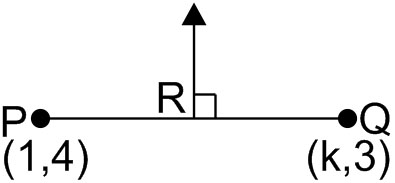
Mid-point of $P Q$ is
$
R\left(\frac{k+1}{2}, \frac{7}{2}\right)
$

Slope of $P Q$ is $\frac{1}{1-k}$
The slope of a line perpendicular to $P Q=(k-1)$
$
\begin{aligned}
& \left(y-\frac{7}{2}\right)=(k-1)\left(x-\left(\frac{k+1}{2}\right)\right) \\
& y \text {-intercept }=-4, \text { so point is }(0,-4) \\
& \left(-4-\frac{7}{2}\right)=(k-1)\left(-\left(\frac{k+1}{2}\right)\right) \\
& \frac{15}{2}=\frac{(k-1)(k+1)}{2} \\
& k^2=16 \Rightarrow k= \pm 4
\end{aligned}
$

Hence, the required answer is 4

Example 4: P is a point on either of the two lines $y-\sqrt{3}|x|=2$ at a distance of 5 units from their point of intersection. The coordinates of the foot of the perpendicular from P on the bisector of the angle between them are :

Solution: The distance between the point $A\left(x_1, y_1\right)$ and $B\left(x_2, y_2\right)$ is $\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}$

$\begin{aligned} & \text { for } x>0 ; y \sqrt{3}-x-2=0 \\ & x<0 ; y+\sqrt{3} x-2=0\end{aligned}$

$
P=\left(\frac{5}{2}, \frac{4+5 \sqrt{3}}{2}\right)_{\text {or }}\left(-\frac{5}{2}, \frac{4+5 \sqrt{3}}{2}\right)
$
distance of $p$ on its angle bisector i.e. $y$-axis is $\left(0, \frac{4+5 \sqrt{3}}{2}\right)$

Hence, the required answer is
$
\left(0, \frac{4+5 \sqrt{3}}{2}\right)
$

Example 5: The equation of the bisector of the angle between the lines $x+y=1$ and $7 x-y=3$ that contain the point $(2,3)$ is
Solution: Equation of bisector:
$
\left|\frac{\mathrm{x}+\mathrm{y}-1}{\sqrt{2}}\right|=\left|\frac{7 \mathrm{x}-\mathrm{y}-3}{\sqrt{50}}\right|
$

Now at $(2,3), \mathrm{x}+\mathrm{y}-1>0$ and $7 \mathrm{x}-\mathrm{y}-3>0$.
Hence the equation of bisector contains the point $(2,3)$ is $\frac{x+y-1}{\sqrt{2}}=\frac{7 x-y-3}{\sqrt{50}}$
Hence, the answer is $x-3 y+1=0$

Summary

The concept of an angle bisector is fundamental in geometry, dividing angles into two equal parts. Angle bisectors play a crucial role in various applications, such as solving triangle properties to architectural design and navigation. Understanding their properties enriches our ability to analyze and solve complex problems.

Frequently Asked Questions (FAQs)

Q1) What is an angle Bisector?

Answer: The Locus of point which is equidistant from both lines is called the angle bisector. The bisector is the locus of a point that moves in the plane of lines $L_1$ and $L_2$ such that lengths of perpendiculars drawn from it to the two given lines $\left(L_1\right.$ and $\left.L_2\right)$ are equal.

Q2) What is the equation of angle bisectors?
Answer: The equation of the angle bisectors between the two lines
$
\begin{aligned}
& \mathrm{L}_1=\mathrm{a}_1 \mathrm{x}+\mathrm{b}_1 \mathrm{y}+\mathrm{c}_1=0 \text { and } \mathrm{L}_2=\mathrm{a}_2 \mathrm{x}+\mathrm{b}_2 \mathrm{y}+\mathrm{c}_2=0 \text { is } \\
& \frac{\left(\mathbf{a}_1 \mathbf{x}+\mathbf{b}_1 \mathbf{y}+\mathbf{c}_1\right)}{\sqrt{\mathbf{a}_{\mathbf{1}}^2+\mathbf{b}_{\mathbf{1}}^2}}= \pm \frac{\left(\mathbf{a}_2 \mathbf{x}+\mathbf{b}_2 \mathbf{y}+\mathbf{c}_2\right)}{\sqrt{\mathbf{a}_{\mathbf{2}}^2+\mathbf{b}_{\mathbf{2}}^2}}
\end{aligned}
$

Q3) What is the equation of the bisector of the angle containing the origin?
Answer: The equation of the bisector of the angle containing the origin
$
\frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{a_1^2+b_1^2}}=\frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{a_2^2+b_2^2}}
$

Q4) What is the condition for an acute angle bisector?

Answer: Let the angle between this bisector and one of the given lines be $\Theta / 2$, where $\Theta$ is an angle between lines containing these bisectors.
$
\begin{aligned}
&\theta<\pi / 2 \\
& \Rightarrow \quad \theta / 2<\pi / 4 \\
& \Rightarrow \quad|\tan (\theta / 2)|<1 \\
& \Rightarrow \quad \tan (\angle \mathrm{ROB})<1
\end{aligned}
$

Q5) What is the condition for an obtuse angle bisector?

Answer: Let the angle between this bisector and one of the given lines be $\Theta / 2$, where $\theta$ is an angle between lines containing these bisectors.ROB is the bisector of an obtuse angle if, $\mid$ tan ( $\theta / 2$ ) $>1$