Equations of Normal in Ellipse

An ellipse is the locus of a point which moves such that its distance from a fixed point (focus) is a constant. Tangent of an ellipse is a line which touches the ellipse at only one point. The normal is a line perpendicular to the tangent and passing through the point of contact to the ellipse.

This article is about the equation of normal in point form and parametric form which falls under the broader category of two dimensional analytical Geometry. This concept has applications in various fields like calculus, physics etc. In real life, we use ellipses in race tracks, architectural design, mirrors, and celestial orbits etc. This is one of the important topics for competitive exams. In JEE MAINS( 2013 to 2023), questions were from this topic including one in 2013, one in 2017, and three in 2022.

Equation of Normal in Point Form

The normal is a line perpendicular to the tangent and passing through the point of contact to the ellipse. The equation of normal at $\left(x_1, y_1\right)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is

$
\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2 .
$

Derivation of Equation of Normal in Point Form

We know that the equation of tangent in point from at $\left(\mathrm{x}_1, \mathrm{y}_1\right)$

$
\frac{x x_1}{a^2}+\frac{y y_1}{b^2}=1
$

Slope of tangent at $\left(x_1, y_1\right)$ is $-\frac{b^2 x_1}{a^2 y_1}$
$\therefore \quad$ Slope of normal at $\left(x_1, y_1\right)$ is $\frac{\mathrm{a}^2 \mathrm{y}_1}{\mathrm{~b}^2 \mathrm{x}_1}$
Hence, the equation of normal at point $\left(\mathrm{x}_1, \mathrm{y}_1\right)$ is

$
\left(\mathrm{y}-\mathrm{y}_1\right)=\frac{\mathrm{a}^2 \mathrm{y}_1}{\mathrm{~b}^2 \mathrm{x}_1}\left(\mathrm{x}-\mathrm{x}_1\right)
$

$b^2x_1(y-y_1) = ab^2y_1(x-x_1)$

$\text { or } \quad \frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2
$

Equation of Normal in Parametric form

The equation of normal at $(a \cos \theta, b \sin \theta)$ to the ellipse, $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is $ax \sec \theta-b y \csc \theta=a^2-b^2$

Derivation of Equation of Normal in Parametric form

In the equation of point form of normal, replace $x_1$ with a. $\cos \theta$ and $y_1$ with $b \cdot \sin \theta$.

$
\begin{aligned}
& \frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2 \\
& \mathrm{x}_1 \rightarrow a \cos \theta \\
& \mathrm{y}_1 \rightarrow b \sin \theta \\
& \frac{a^2 x}{a \cos \theta}-\frac{b^2 y}{b \sin \theta}=a^2-b^2 \\
& \mathrm{ax} \sec \theta-b y \csc \theta=a^2-b^2
\end{aligned}
$

Recommended Video Based on Equation of the Normal to Ellipse

Solved Examples Based on Equation of the Normal to Ellipse

Example 1: If the normal to the ellipse $3 x^2+4 y^2=12$ at a point P on its parallel to the line, $2 x+y=4$ and the tangent to the ellipse at P passes through $Q(4,4)$ then PQ is equal to :
1)$
\frac{\sqrt{157}}{2}
$

2)$
\frac{\sqrt{221}}{2}
$

3)$
\frac{\sqrt{61}}{2}
$

4) $\frac{5 \sqrt{5}}{2}$

Solution

Equation of Norma to ellipse -
The equation of normal at $\left(\mathrm{x}_1, \mathrm{y}_1\right)$ to the ellipse, $\frac{\mathrm{A}}{\mathrm{a}^2}+\frac{y}{\mathrm{~b}^2}=1$ is $\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2$.

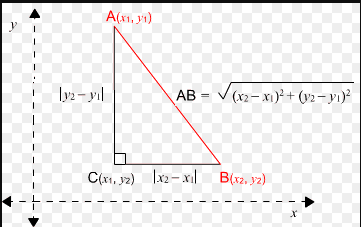
Distance formula -
The distance between the point $A\left(x_1, y_1\right)$ and $B\left(x_2, y_2\right)$
is $\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}$
- wherein

$
\begin{aligned}
& 3 x^2+4 y^2=12 \\
& \frac{x^2}{4}+\frac{y^2}{3}=1
\end{aligned}
$

So, $x=2 \cos \theta \quad y=\sqrt{3} \sin \theta$
Let $\quad P(2 \cos \theta, \sqrt{3} \sin \theta)$
Equation of normal is $\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2$

$
\begin{aligned}
& \frac{4 x}{2 \cos \theta}-\frac{3 y}{\sqrt{3} \sin \theta}=4-3 \\
& 2 x \sin \theta-\sqrt{3} y \cos \theta=\cos \theta \sin \theta \\
& \text { Slope }=\frac{2}{\sqrt{3}} \tan \theta=-2 \\
& \tan \theta=-\sqrt{3}
\end{aligned}
$

Equation of tangent is it passes through $(4,4)$
$12 \cos \theta+8 \sqrt{3} \sin \theta=6$

$
\begin{aligned}
& \frac{1}{2} \cos \theta+\frac{8 \sqrt{3}}{6} \sin \theta=1 \\
& \cos \theta=-\frac{1}{2}, \quad \sin \theta=\frac{\sqrt{3}}{2} \quad \therefore \theta=120^{\circ}
\end{aligned}
$

Hence point is $(2 \cos 120, \sqrt{3} \sin 120)$

$
\begin{aligned}
& P\left(-1, \frac{3}{2}\right), Q(4,4) \\
& P Q=\sqrt{(-1-4)^2+\left(\frac{3}{2}-4\right)^2}=\sqrt{25+\frac{25}{4}} \\
& =\frac{5 \sqrt{5}}{2}
\end{aligned}
$

Example 2: Let the tangents at the points P and Q on the ellipse $\frac{\mathrm{x}^2}{2}+\frac{\mathrm{y}^2}{4}=1$ meet at the point $\mathrm{R}(\sqrt{2}, 2 \sqrt{2}-2)$. If S is the focus of the ellipse on its negative major axis, then $\mathrm{SP}^2+\mathrm{SQ}^2$ is equal to $\qquad$
MAINS 2022]
Solution
Equation of chard of contact is $\mathrm{T}=0$

$
\begin{aligned}
& \Rightarrow \quad \frac{\sqrt{2} \mathrm{x}}{2}+\frac{(2 \sqrt{2}-2) \mathrm{y}}{4}=1 \\
& \Rightarrow \quad 2 \sqrt{2} \mathrm{x}+(2 \sqrt{2}-2) \mathrm{y}=4 \\
& \Rightarrow \quad \mathrm{x}=\frac{4-(2 \sqrt{2}-2) \mathrm{y}}{2 \sqrt{2}}
\end{aligned}
$
Finding point of intersection with ellipse

$
\begin{aligned}
& \frac{(4-(2 \sqrt{2}-2) \mathrm{y})^2}{8 \times 2}+\frac{y^2}{4}=1 \\
& \Rightarrow \frac{(2-(\sqrt{2}-1) \mathrm{y})^2}{4}+\frac{\mathrm{y}^2}{4}=1 \\
& \Rightarrow \quad 4+(\sqrt{2}-1)^2 \mathrm{y}^2-4(\sqrt{2}-1) \mathrm{y}+\mathrm{y}^2=4 \\
& \Rightarrow \quad(3-2 \sqrt{2}+1) \mathrm{y}^2-4(\sqrt{2}-1) \mathrm{y}=0 \\
& \Rightarrow \quad 2 \sqrt{2}(\sqrt{2}-1) \mathrm{y}^2-4(\sqrt{2}-1) \mathrm{y}=0 \\
& \Rightarrow 2 \sqrt{2}(\sqrt{2}-1) \mathrm{y}(\mathrm{y}-\sqrt{2})=0 \\
& \Rightarrow \mathrm{y}=0, \sqrt{2} \\
& \Rightarrow \mathrm{x}=\sqrt{2}, 1
\end{aligned}
$

$
\begin{aligned}
& \frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2 e^2 \\
& \frac{a^2 x}{a e}-\frac{b^2 y}{b^2} \cdot a=a^2 e^2 \\
& \frac{a x}{e}-a y=a^2 e^2 \Rightarrow \frac{x}{e}-y=a e^2
\end{aligned}
$

passes through $(0, b)$

$
\begin{aligned}
-b=a e^2 & \Rightarrow b^2=a^2 e^4 \\
a^2\left(1-e^2\right) & =a^2 e^4 \Rightarrow e^4+e^2=1
\end{aligned}
$

$
\begin{aligned}
& \Rightarrow \mathrm{x}=\sqrt{2}, 1 \\
& \therefore \mathrm{P}(\sqrt{2}, 0), \mathrm{Q}(1, \sqrt{2})
\end{aligned}
$
S is $(0,-\mathrm{be})$

$
\begin{aligned}
& \mathrm{e}=\sqrt{1-\frac{2}{4}}=\frac{1}{\sqrt{2}} \\
& \therefore \mathrm{S} \text { is }(0,-\sqrt{2}) \\
& \therefore \mathrm{PS}^2+\mathrm{SQ}^2=4+9=13
\end{aligned}
$

Hence, the answer is 13 .

Example 3: If the normal at the point $\mathrm{P}(\theta)$ to the ellipse $\frac{\mathrm{x}^2}{14}+\frac{\mathrm{y}^2}{5}=1$ intersects it again at the point $\mathrm{Q}(2 \theta)$, then $\cos \theta$ is equal to
1) $2 / 3$
2) $-2 / 3$
3) $3 / 4$
4) None of these

Solution

$
\begin{aligned}
& \frac{\sqrt{14} \mathrm{x}}{\cos \theta}-\frac{\sqrt{5} \mathrm{y}}{\sin \theta}=14-5 ; \text { as it passes through }(\sqrt{14} \cos 2 \theta, \sqrt{5} \sin 2 \theta) \\
& \text { so, } \frac{14\left(2 \cos ^2 \theta-1\right)}{\cos \theta}-\frac{5 \times 2 \sin \theta \cos \theta}{\sin \theta}=9 \\
& \Rightarrow 28 \cos \theta-\frac{14}{\cos \theta}-10 \cos \theta=9 \\
& \Rightarrow 18 \cos ^2 \theta-9 \cos \theta-14=0 \\
& \Rightarrow(3 \cos \theta+2)(6 \cos \theta-7)=0 \Rightarrow \cos \theta=-\frac{2}{3}
\end{aligned}
$
Hence, the answer is the option (2).

Example 4: Let the ellipse, $\frac{\mathrm{x}^2}{\mathrm{a}^2}+\frac{\mathrm{y}^2}{\mathrm{~b}^2}=1, \mathrm{a}>\mathrm{b}$, pass through the point $(2,3)$ and have eccentricity equal to $\frac{1}{2}$. Then, the equation of the normal to the ellipse at $(2,3)$ is:
[JEE MAINS 2020]
Solution
The equation of normal of slope $m$ to the ellipse, $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ are $y=m x \mp \frac{m\left(a^2-b^2\right)}{\sqrt{a^2+m^2 b^2}}$ and coordinate of point of contact is

$
\begin{gathered}
\left( \pm \frac{a^2}{\sqrt{a^2+m^2 b^2}}, \pm \frac{m b^2}{\sqrt{a^2+m^2 b^2}}\right) \\
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\end{gathered}
$
Equation of tanget at $(2,3)=\frac{2 x}{a^2}+\frac{3 y}{b^2}=1$
slope of Tangent $m_t=\frac{-b^2}{a^2} \times \frac{2}{3}$
Now $e=\sqrt{1-\frac{b^2}{a^2}} \Rightarrow \frac{b^2}{a^2}=\frac{3}{4}$
Slope of Normal $m_N=2$
Hence, the answer is 2

Example 5: Let the line $\mathrm{y}=\mathrm{mx}$ and the ellipse $2 x^2+y^2=1$ intersect at a point P in the first quadrant. If the normal to this ellipse at P meets the co-ordinate axes at $\left(-\frac{1}{3 \sqrt{2}}, 0\right)$ and $(0, \beta)$, then $\beta$ is equal to :
$[$ JEE
MAINS 2022]
Solution
Let $P$ be $\left(x_1, y_1\right)$
Equation of normal at $P$ is $\frac{x}{2 x_1}-\frac{y}{y_1}=-\frac{1}{2}$
It passes through $\left(-\frac{1}{3 \sqrt{2}}, 0\right) \Rightarrow \frac{-1}{6 \sqrt{2} x_1}=-\frac{1}{2} \Rightarrow x_1=\frac{1}{3 \sqrt{2}}$
So $y_1=\frac{2 \sqrt{2}}{3}($ as $P$ lies in 1 'quadrant $)$
So $\beta=\frac{y_1}{2}=\frac{\sqrt{2}}{3}$
Hence, the answer is $\frac{\sqrt{2}}{3}$

Summary

The normal is a line perpendicular to the tangent and passing through the point of contact to the ellipse.Understanding the concepts of ellipse helps in solving hte more complex problems not in mathematics but also in physics, engineering, astronomy etc.