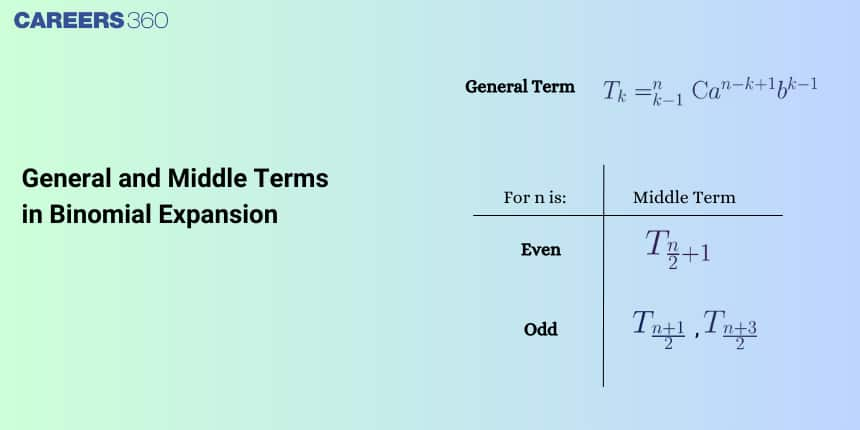General and Middle Terms in Binomial Expansion

General Term in Binomial Expansion

A binomial expression is any algebraic expression containing exactly two terms. These expressions commonly appear in algebra, JEE-level questions, CUET exams, and competitive math problems.

Examples of binomial expressions include:
$ (a+b)^2,\ \left(\sqrt{x}+\dfrac{k}{x^2}\right)^5,\ (x+9y)^{-2/3} $

When expanding $(x+y)^n$, we often need only one specific term instead of the full expansion. The $(r+1)^{\text{th}}$ term is called the general term, given by:

$T_{r+1} = {}^nC_r \cdot x^{n-r} \cdot y^r$

This formula helps quickly extract any required term—very helpful in competitive exams.

Term Independent of $x$

A term is independent of $x$ when its power of $x$ becomes zero, i.e., $x^0$.

Example: Find the term independent of $x$ in $(x - \dfrac{1}{x})^{20}$.

[
T_{r+1} = {}^{20}C_r \cdot x^{20-r} \cdot (-1)^r \cdot x^{-r}
]

[
T_{r+1} = {}^{20}C_r \cdot x^{20 - 2r} \cdot (-1)^r
]

To make exponent of $x$ equal to zero:

$20 - 2r = 0 \Rightarrow r = 10$

So, the term independent of $x$ is the $11^{\text{th}}$ term.

$(p+1)$th Term From the End

The binomial expansion of $(x+y)^n$ is:

$ {}^nC_0 x^n + {}^nC_1 x^{n-1}y + {}^nC_2 x^{n-2}y^2 + \cdots + {}^nC_n y^n $

From the Beginning

$ \underbrace{{}^nC_0 x^n}{1^{st}} + \underbrace{{}^nC_1 x^{n-1}y}{2^{nd}} + \underbrace{{}^nC_2 x^{n-2}y^2}{3^{rd}} + \cdots + \underbrace{{}^nC_n y^n}{(n+1)^{th}} $

From the End

$ \underbrace{{}^nC_0 y^n}{1^{st}} + \underbrace{{}^nC_1 y^{n-1}x}{2^{nd}} + \underbrace{{}^nC_2 y^{n-2}x^2}{3^{rd}} + \cdots + \underbrace{{}^nC_n x^n}{(n+1)^{th}} $

Using the identity:

$ {}^nC_r = {}^nC_{n-r} $

So the $(p+1)^{\text{th}}$ term from the end of $(x+y)^n$ equals the $(p+1)^{\text{th}}$ term from the beginning of $(y+x)^n$:

$ T_{p+1} = {}^nC_p \cdot y^{,n-p} \cdot x^p $

Radical-Free or Rational Terms

In an expansion like $(x^{1/a} + y^{1/b})^N$, a term is rational only if the exponents of $x$ and $y$ are integers.

General term:

$T_{r+1} = {}^N C_r \cdot x^{\frac{N-r}{a}} \cdot y^{\frac{r}{b}}$

Example: Number of rational terms in $(\sqrt[4]{9} + \sqrt[6]{8})^{100}$

Rewrite in prime form:

$\sqrt[4]{9} = 3^{1/2}$
$\sqrt[6]{8} = 2^{1/2}$

General term:

$T_{r+1} = {}^{100}C_r \cdot 3^{50 - r/2} \cdot 2^{r/2}$

For the indices to be integers:

$\dfrac{r}{2} \in \mathbb{Z} \Rightarrow r$ must be even.

Possible values:
$r = 0, 2, 4, …, 100$

Number of values = $50 + 1 = 51$

So, 51 rational terms exist.

Middle Term in Binomial Expansion

The middle term(s) depend on whether $n$ is even or odd.

Case 1: $n$ Even

Total terms = $n+1$ → odd → one middle term

Position:

$\left(\dfrac{n}{2} + 1\right)^{th}$

Middle term:

$T_{\frac{n}{2}+1} = \binom{n}{\frac{n}{2}} x^{\frac{n}{2}} y^{\frac{n}{2}}$

Case 2: $n$ Odd

Total terms = $n+1$ → even → two middle terms

Positions:

$\left(\dfrac{n+1}{2}\right)^{th},\quad \left(\dfrac{n+3}{2}\right)^{th}$

Values:

$T_{\frac{n+1}{2}} = \binom{n}{\frac{n-1}{2}} x^{\frac{n+1}{2}} y^{\frac{n-1}{2}}$

$T_{\frac{n+3}{2}} = \binom{n}{\frac{n+1}{2}} x^{\frac{n-1}{2}} y^{\frac{n+1}{2}}$

Note on Largest Binomial Coefficient

• If $n$ is even, the maximum value occurs at ${}^nC_{n/2}$

• If $n$ is odd, the two equal maximum values occur at:
  $ {}^nC_{(n-1)/2} $ and $ {}^nC_{(n+1)/2} $

Solved Examples Based on General and Middle Terms in Binomial Expansion:

Example 1: The sum of the real values of $x$ for which the middle term in the binomial expansion of $\left(\frac{x^3}{3}+\frac{3}{x}\right)^8$ equals 5670 is :
1) 6
2) 4
3) 0
4) 8

Solution: Middle term in Binomial Expression if n is even
$\left(\frac{n}{2}+1\right)_{\text {th term is middle term }}$
And it equals ${ }^n C_{\frac{n}{2}} \cdot x^{\frac{n}{2}} \cdot y^{\frac{n}{2}}$

Now,

The middle term can be written as

$
\begin{aligned}
& T_5={ }^8 C_4\left(\frac{x^3}{3}\right)^4\left(\frac{3}{x}\right)^4=5670 \\
& \Rightarrow 70 x^8=5670 \\
& \Rightarrow x^8=81 \\
& \Rightarrow x= \pm \sqrt{3}
\end{aligned}
$

The sum of real values $=0$
Hence, the answer is the option 3.

Example 2: In the binomial expansion of $(a-b)^n, n \geq 5$, the sum of $5^{\text {th }}$ and $6^{\text {th }}$ terms is zero, then $a / b$ equals:
1) $\frac{n-5}{6}$
2) $\frac{n-4}{5}$
3) $\frac{5}{n-4}$
4) $\frac{6}{n-5}$

Solution

As we learned in

General Term in the expansion of $(x+a)^n$

$
T_{r+1}={ }^n C_r \cdot x^{n-r} \cdot a^r
$

Now,

$
\begin{aligned}
& \text { In }(\mathrm{a}-\mathrm{b})^{\mathrm{n}} \\
& T_5={ }^n C_4(a)^{n-4}(-b)^4 \text { and } T_6={ }^n C_5(a)^{n-5}(-b)^5 \\
& \mathrm{~T}_5+\mathrm{T}_6=0 \\
& { }^n C_4(a)^{n-4}(b)^4={ }^n C_5(a)^{n-5}(b)^5 \\
& \frac{a}{b}=\frac{{ }^n C_5}{{ }^n C_4}=\frac{\frac{n!}{5!(n-5)!}}{\frac{n!}{4!(n-4)!}}=\frac{n-4}{5}
\end{aligned}
$

Hence, the answer is an option (2).

Example 3: The coefficient of $x^7$ in the expansion of $\left(1-x-x^2+x^3\right)^6$ is
1) -144
2) 132
3) 144
4) -132

Solution

As we learnt in

General Term in the expansion of $(x+a)^n$

$
T_{r+1}={ }^n C_r \cdot x^{n-r} \cdot a^r
$

Now,
We have to simplify $\left(1-x-x^2+x^3\right)^6$
We get $\left[(1-x)-x^2(1-x)\right]^6$

$
\begin{aligned}
& =\left[(1-x)\left(1-x^2\right)\right]^6 \\
& =(1-x)^6\left(1-x^2\right)^6
\end{aligned}
$

For a coefficient of $\mathrm{x}^7$ in $(1-x)^6\left(1-x^2\right)^6$

$
\begin{aligned}
& =\left(1-{ }^6 C_1 x+{ }^6 C_2 x^2 \ldots \ldots \ldots \ldots \ldots\right)\left(1-{ }^6 C_1 x^2+{ }^6 C_2 x^4-{ }^6 C_3 x^6 \ldots \ldots \ldots \ldots\right) \\
& ={ }^6 C_1 \cdot{ }^6 C_3-{ }^6 C_3 \cdot{ }^6 C_2+{ }^6 C_5 \cdot{ }^6 C_1 \\
& =120-300+36=-144
\end{aligned}
$
Hence, the answer is the option 1.

Example 4: The term independent of $x$ in expansion of $\left(\frac{x+1}{x^{2 / 3}-x^{1 / 3}+1}-\frac{x-1}{x-x^{1 / 2}}\right)^{10}$ is :
1) 310
2) 4
3) 120
4) 210

Solution

Now,

$
\begin{aligned}
& S=\left(\frac{\left(x^{1 / 3}+1\right)\left(x^{2 / 3}-x^{1 / 3}+1\right)}{\left(x^{2 / 3}-x^{1 / 3}+1\right)}-\frac{\left(x^{1 / 2}-1\right)\left(x^{1 / 2}+1\right)}{x^{1 / 2}\left(x^{1 / 2}-1\right)}\right)^{10} \\
& =\left(\left(x^{1 / 3}+1\right)-\left(1+x^{-1 / 2}\right)\right)^{10} \\
& =\left(x^{1 / 3}-x^{-1 / 2}\right)^{10} \\
& T_{r+1}={ }^{10} C_r\left(x^{1 / 3}\right)^{10-r}\left(-x^{-1 / 2}\right)^r \\
& =(-1)^r \cdot{ }^{10} C_r \cdot x^{\frac{10-r}{3}-\frac{r}{2}}
\end{aligned}
$

For term independent of $x$,

$
\Rightarrow \quad \frac{10-r}{3}-\frac{r}{2}=0 \Rightarrow 5 r=20
$

So, $T_{r+1}={ }^{10} C_4=210$
Hence, the answer is the option (4).

$x^7$ in $\left[a x^2+\left(\frac{1}{b x}\right)\right]^{11}$ equals the coefficient of $x^{-7}$ in $\left[a x-\left(\frac{1}{b x^2}\right)\right]^{11}$, if $a=1 / 2$, then $b=$
1)$1 / 2$
2)1
3) (correct)
2
4)None of these

$
\begin{aligned}
& T_{r+1} \text { of }\left(a x^2+\frac{1}{b x}\right)^{11}={ }^{11} C_r\left(a x^2\right)^{11-r}\left(\frac{1}{b x}\right)^r \\
& T_{r+1} \text { of }\left(a x-\frac{1}{b x^2}\right)^{11}={ }^{11} C_r(a x)^{11-r}\left(-\frac{1}{b x^2}\right)^r
\end{aligned}
$

$\therefore$ Coefficient of $x^7$ in $\left(a x^2+\frac{1}{b x}\right)^{11}={ }^{11} C_5 \frac{a^6}{b^5}$ and coefficient of $x^{-7}$ in $\left(a x-\frac{1}{b x^2}\right)^{11}={ }^{11} C_6 \frac{a^5}{b^6}$ Now ${ }^{11} C_5 \frac{a^6}{b^5}={ }^{11} C_6 \frac{a^5}{b^6} \quad \therefore a b=1$.

Hence, the answer is the option(3).

Last Digits and Remainder using the Binomial Expansion

Greatest Binomial Coefficient