Harmonic Mean in HP

If the terms of a sequence follow some pattern that can be defined by an explicit formula in n, then the sequence is called a progression. We have three types of progression Arithmetic Progression, Geometric progression, and harmonic progression. In real life, we use Harmonic Progression in electrical gadgets, machines, or the generation of power. It is also used to calculate the degree to which water boils when its temperature increases by the same amount.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Harmonic Progression
2. Important Property of HM
3. Summary
4. Problem Based on Mean of Harmonic Progression

In this article, we will cover the concept of the Harmonic mean in HP. This category falls under the broader category of Sequence and series, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. A total of nine Questions based on this topic have been asked in JEE Mains including one in 2021.

Harmonic Progression

Harmonic Progression is a progression of real values which when reciprocal form arithmetic progression except for zero.

A sequence $a_1, a_2, a_3, \ldots, a_n, \ldots$ of non-zero numbers is called a harmonic progression if the sequence is an arithmetic progression.
OR
Reciprocals of arithmetic progression is a Harmonic progression.
E.g., $\frac{1}{2}, \frac{1}{5}, \frac{1}{8}, \frac{1}{11}$,. is an HP because their reciprocals $2,5,8,11, \ldots$ form an A.P.
- No term of the H.P. can be zero.
- The general form of HP is
$
\frac{1}{a}, \frac{1}{a+d}, \frac{1}{a+2 d}, \frac{1}{a+3 d} \ldots .
$

Here a is the first term and d is the common difference of corresponding A.P.

The general term of a Harmonic Progression

The nth term or general term of an H.P. is the reciprocal of the nth term of the corresponding A.P.

Thus, if $a_1, a_2, a_3, \ldots . ., a_n$ is an H.P. and the common difference of corresponding A.P. is d, i.e. $d=\frac{1}{a_n}-\frac{1}{a_{n-1}}$, then the nth term of corresponding AP is $\frac{1}{a_1}+(n-1) d$ and hence, the general term or nth term of an H.P. is given by $\quad \frac{1}{\mathrm{a}_{\mathrm{n}}=\frac{1}{a_1}+(\mathrm{n}-1) \mathrm{d}}$

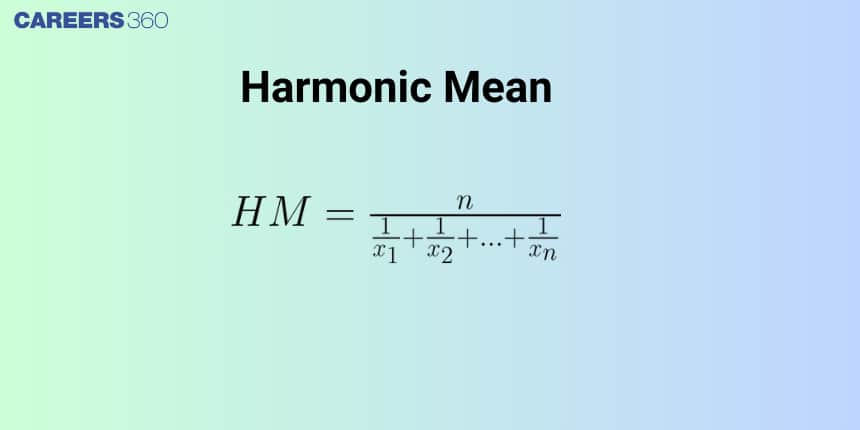
Harmonic Mean

The mean of the given Harmonic Progression is called the Harmonic Mean.

If $a_1, a_2, a_3, \ldots, a_n$ are $n$ positive numbers, then the Harmonic Mean of these numbers is given by $H=\frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+\ldots+\frac{1}{a_n}}$.
If $a$ and $b$ are two numbers and $\mathrm{H}$ is the $\mathrm{HM}$ of $\mathrm{a}$ and $\mathrm{b}$. Then, $\mathrm{a}, \mathrm{H}$, and $b$ are in harmonic progression. Hence, Harmonic mean is given by
$
\mathrm{H}=\frac{2}{\frac{1}{a}+\frac{1}{b}}=\frac{2 a b}{a+b}
$

Note that if the AM between two numbers $\mathrm{a}$ and $\mathrm{b}$ is $\frac{a+b}{2}$, it does NOT follow that HM between the same numbers is $\underline{\frac{2}{a+b}}$. The HM is the reciprocal of $\frac{\frac{1}{a}+\frac{1}{b}}{2}$ i.e. $\frac{2 a b}{a+b}$.

Harmonic mean for discrete data:
Harmonic Mean -for discrete data is given by
$
H=\frac{1}{\sum_{i=1}^n \frac{1}{x_i}}$
Insertion of n-Harmonic Mean Between a and b

Let $\mathrm{H}_1, \mathrm{H}_2, \mathrm{H}_3 \ldots, \mathrm{H}_{\mathrm{n}}$ be $\mathrm{n}$ harmonic mean between two numbers $\mathrm{a}$ and $\mathrm{b}$. Then, $a, \mathrm{H}_1, \mathrm{H}_2, \mathrm{H}_3, \ldots, \mathrm{H}_{\mathrm{n}}, b_{\text {is in H.P. }}$. Hence, $\frac{1}{a}, \frac{1}{\mathrm{H}_1}, \frac{1}{\mathrm{H}_2}, \ldots, \frac{1}{\mathrm{H}_{\mathrm{n}}}, \frac{1}{b}$ are in A.P.

Clearly, this H.P. contains $n+2$ terms.
Let, $\mathrm{D}$ be the common difference of this A.P. Then,
$
\begin{aligned}
& \therefore \frac{1}{\mathrm{~b}}=(n+2)^{\text {th }} \text { term of } \mathrm{AP} \\
& \Rightarrow \frac{1}{\mathrm{~b}}=\frac{1}{\mathrm{a}}+(\mathrm{n}+1) \mathrm{D} \\
& \Rightarrow \mathrm{D}=\frac{\mathrm{a}-\mathrm{b}}{(\mathrm{n}+1) \mathrm{ab}}
\end{aligned}
$

Important Property of HM

The sum of reciprocals of n harmonic means between two numbers is n times the reciprocal of a single H.M. between them.

Proof:

Let $\mathrm{H}_1, \mathrm{H}_2, \mathrm{H}_3 \ldots, \mathrm{H}_{\mathrm{n}}$ be $\mathrm{n}$ harmonic means between two numbers a and $\mathrm{b}$. Then, $a, \mathrm{H}_1, \mathrm{H}_2, \mathrm{H}_3 \ldots, \mathrm{H}_{\mathrm{n}}, b$ is an H.P.
$
\begin{aligned}
\therefore \frac{1}{\mathrm{H}_1} & +\frac{1}{\mathrm{H}_2}+\frac{1}{\mathrm{H}_3}+\ldots+\frac{1}{\mathrm{H}_{\mathrm{n}}}=\frac{\mathrm{n}}{2}\left(\frac{1}{\mathrm{H}_1}+\frac{1}{\mathrm{H}_{\mathrm{n}}}\right) \\
& =\frac{\mathrm{n}}{2}\left(\frac{1}{\mathrm{a}}+\mathrm{D}+\frac{1}{\mathrm{~b}}-\mathrm{D}\right)=\frac{\mathrm{n}}{2}\left(\frac{1}{\mathrm{a}}+\frac{1}{\mathrm{~b}}\right) \\
& =\frac{\mathrm{n}}{[\mathrm{H} . \mathrm{S} . \text { of } a \text { and } b]}
\end{aligned}
$

Summary

In conclusion, harmonic progression is a versatile mathematical concept with wide-ranging applications and intriguing properties. Its study enriches understanding of sequences and series, offering connections to diverse areas of mathematics and beyond. It provides an understanding of reciprocal sequences making it suitable for versatile uses.

Recommended Video :

Problem Based on Mean of Harmonic Progression

Example 1: A man is walking in a straight line. The arithmetic mean of the reciprocals of the intercepts of this line on the coordinate axes $\frac{1}{4}$. Three stones $\mathrm{A}, \mathrm{B}$, and $\mathrm{C}$ are placed at points $(1,1),(2,2)$, and $(4,4)$ respectively. Then which of these stones is/are on the path of man? [JEE MAINS 2021]

Solution

$
\begin{aligned}
& \frac{x}{a}+\frac{y}{b}=1 \\
& \frac{\mathrm{h}}{\mathrm{a}}+\frac{\mathrm{k}}{\mathrm{b}}=1 \\
& \frac{\frac{1}{\mathrm{a}}+\frac{1}{\mathrm{~b}}}{2}=\frac{1}{4} \\
& \therefore \frac{1}{\mathrm{a}}+\frac{1}{\mathrm{~b}}=\frac{1}{2}
\end{aligned}
$
$\therefore$ Line passes through fixed point $(2,2)$ (from (1) and (2))

Stone B is on the path of Man.

Hence, the required answer is B.

Example 2: If the system of linear equations $x+2 a y+a z=0, \quad x+3 b y+b z=0, \quad x+4 c y+c z=0$ has a non-zero solution, then $a, b, c$

Solution: The harmonic mean (HM) of two numbers $a$ and $b$ are given by
$
\begin{aligned}
& H M=\frac{2 a b}{a+b} \\
& x+2 a y+a z=0 \\
& x+3 b y+b z=0 \\
& x+4 c y+c z=0 \\
& \Rightarrow\left|\begin{array}{lll}
1 & 2 a & a \\
1 & 3 b & b \\
1 & 4 c & c
\end{array}\right|=0 \\
& \Rightarrow\left|\begin{array}{ccc}
0 & 2 a-3 b & a-b \\
0 & 3 b-4 c & b-c \\
1 & 4 c & c
\end{array}\right|=0 \\
& \Rightarrow(b-c)(2 a-3 b)-(a-b)(3 b-4 c)=0 \\
& \Rightarrow(b-c)(2 a-3 b)=(a-b)(3 b-4 c) \\
& \Rightarrow 2 a c=a b+b c \\
&
\end{aligned}
$

Dividing by abc we get,
$
\frac{2}{b}=\frac{1}{a}+\frac{1}{c}
$

Therefore, a, b, and c are in HP.

Hence, the required answer is a,b, and c are in HP.

Example 3: If $\mathrm{H}$ is the harmonic mean between $\mathrm{p}$ and $\mathrm{q}$, then the value of $\frac{H}{p}+\frac{H}{q}$ is
Solution The harmonic mean ( $\mathrm{HM}$ ) of two numbers $a$ and $b$ are given by
$
H M=\frac{2 a b}{a+b}
$

Given $\mathrm{H}$ is hormonic mean of $\mathrm{p}$ and $\mathrm{q}$
$
\begin{aligned}
& \frac{2}{H}=\frac{1}{p}+\frac{1}{q} \\
& H=\frac{2 p q}{p+q} \\
& \text { Hence, } \frac{H}{p}+\frac{H}{q}=H\left(\frac{1}{p}+\frac{1}{q}\right) \\
& =H \times \frac{2}{H} \\
& =2
\end{aligned}
$

Hence, the required answer is 2.

Example 4: Let $R_1$ and $R_2$ respectively be the maximum ranges up and down on an inclined plane and $R$ be the maximum range on the horizontal plane. Then, $R_1, R, R_2$ are in:
Solution
Let $\theta$ be the angle of inclination of the plane to horizontal and $u$ be the velocity of projection of the projectile
$
\begin{array}{ll}
\therefore & R_1=\frac{u^2}{g(1+\sin \theta)}, R_2=\frac{u^2}{g(1-\sin \theta)} \\
\therefore & \frac{1}{R_1}+\frac{1}{R_2}=\frac{2 g}{u^2}=\frac{2}{R} \\
\Rightarrow & R_1, R_1, R_2 \in H . P .
\end{array}
$

Hence the answer is $R_1, R, R_2$ are in HP.
Example 5: What is the value of HM of data $3,9,18,27$ ?
Solution Harmonic Mean -for discrete data is given by
$
\begin{aligned}
& H=\frac{1}{\sum_{i=1}^n \frac{1}{x_i}} \\
& H M=\frac{4}{\frac{1}{3}+\frac{1}{9}+\frac{1}{18}+\frac{1}{27}}=\frac{4}{\frac{18+3+6+2}{54}} \\
& =\frac{4 \times 54}{29}=\frac{216}{29}=7.44
\end{aligned}
$

Hence the required answer is 7.44.

Frequently Asked Questions (FAQs)

Q1) What is harmonic Progression?
Answer: Harmonic Progression is a progression of real values which when reciprocal form arithmetic progression except for zero.
Q2) Find the harmonic mean of $4,8,16$.

Answer: H.M. of $4,8,16$ $
=\frac{3}{\frac{1}{4}+\frac{1}{8}+\frac{1}{16}}
$
$
\begin{aligned}
& =\frac{48}{7} \\
& =6.85
\end{aligned}
$

Q3) If $a$ and $b$ are two numbers, then what is the harmonic mean of $a$ and $b$ ?
Answer: If $a$ and $b$ are two numbers and $H$ is the $H M$ of $a$ and $b$. Then, $a, H$, and $b$ are in harmonic progression. Hence, the Harmonic mean is given by
$
\mathrm{H}=\frac{2}{\frac{1}{a}+\frac{1}{b}}=\frac{2 a b}{a+b}
$

Q4) What is the difference between Harmonic Progression and Arithmetic Progression?

Answer: An arithmetic progression is a sequence in which each term increases or decreases by a constant term or fixed number. whereas Harmonic Progression is a progression of real values which when reciprocal form arithmetic progression except for zero.

Q5)State whether we can determine the Harmonic Progression graphically or not.

Answer: No, we can not determine the Harmonic Progression graphically.