Higher Order derivatives

Higher order Differentiation is one of the important parts of Calculus, which applies to measuring the change in the function at a certain point. Mathematically, it forms a powerful tool by which slopes of functions are determined, the maximum and minimum of functions found, and problems on motion, growth, and decay, to name a few. These concepts of differentiation have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Derivative of a Function
2. Properties of derivative of a function
3. Higher Order Derivative of a Function
4. Solved Exampled Based on Higher Order Derivatives
5. Summary

In this article, we will cover the concept of higher-order derivative of a Function. This concept falls under the broader category of Calculus, a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last five years of the JEE Main exam (from 2013 to 2023), a total of nine questions have been asked on this concept, including one in 2020, two in 2021, two in 2022, and four in 2023.

Function:

$A$ and $B$ are two non-empty sets, then a relation from $A$ to $B$ is said to be a function if each element $x$ in $A$ is assigned a unique element $f(x)$ in $B$, and it is written as
$f: A \rightarrow B$ and read as $f$ is a mapping from $A$ to $B$.

Derivative of a Function

Let $f$ be defined on an open interval $I \subseteq$ containing the point $x_0$, and suppose that $\lim _{\Delta x \rightarrow 0} \frac{f\left(x_0+\Delta x\right)-f\left(x_0\right)}{\Delta x}$ exists. Then $f$ is said to be differentiable at $x_0$ and the derivative of $f$ at $x_0$, denoted by $f^{\prime}\left(x_0\right)$, is given by

$
f^{\prime}\left(x_0\right)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_0+\Delta x\right)-f\left(x_0\right)}{\Delta x}
$

For all $x$ for which this limit exists,
$f^{\prime}(x)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}$ is a function of $x$.

In addition to $f^{\prime}(x)$, other notations are used to denote the derivative of $y=f(x)$. The most common notations are $f^{\prime}(x), \frac{d y}{d x}, y^{\prime}, \frac{d}{d x}[f(x)], D_x[y]$ or $D y$ or $y_1$. Here $\frac{d}{d x}$ or $D$ is the differential operator.

Properties of derivative of a function

1. The derivative of sum of two functions is equal to the sum of their derivatives.

(i.e)., $\frac{d}{dx}[f(x)+g(x)] = \frac{d}{dx}[f(x)]+\frac{d}{dx}[g(x)]$

2. The derivative of differnce betweeen two functions is equal to the difference between their derivatives.

(i.e)., $\frac{d}{dx}[f(x)+g(x)] = \frac{d}{dx}[f(x)]+\frac{d}{dx}[g(x)]$

3. The derivative of the product of two functions is given by

$\frac{d}{dx}[f(x)g(x)] = (\frac{d}{dx}f(x))g(x)+f(x)(\frac{d}{dx}g(x))$

4. The derivative of the quotient of two functions is given by

$\frac{d}{dx}[\frac{f(x)}{g(x)}] = \frac{(\frac{d}{dx}f(x))g(x)+f(x)(\frac{d}{dx}g(x))}{(g(x))^2}$

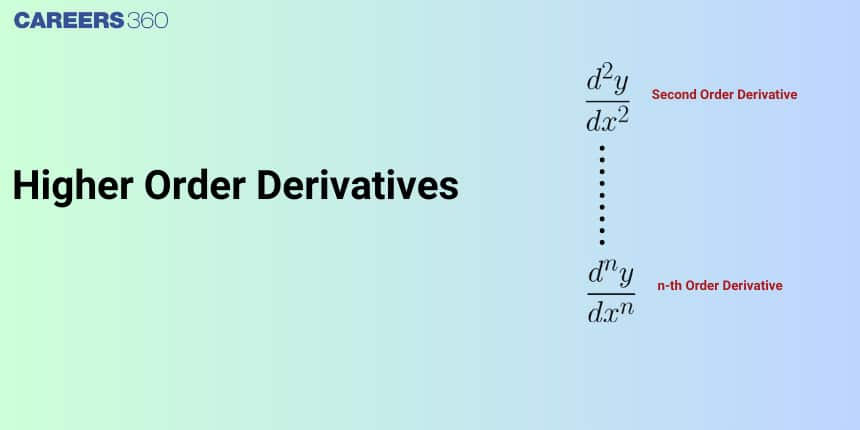
Higher Order Derivative of a Function

The derivative of a function is itself a function, so we can find the derivative of a derivative. The new function obtained by differentiating the derivative is called the second derivative. Furthermore, we can continue to take derivatives to obtain the third derivative, a fourth derivative, and so on.

Collectively, these are referred to as higher-order derivatives. The notation for the higher-order derivatives of $y=f(x)$ can be expressed in any of the following forms:

$
\begin{aligned}
& f^{\prime}(x), f^{\prime \prime}(x), f^{\prime \prime \prime}(x), f^{(4)}(x), \ldots, f^{(n)}(x) \\
& y^{\prime}, y^{\prime \prime}(x), y^{\prime \prime \prime}(x), y^{(4)}(x), \ldots, y^{(n)}(x) \\
& \frac{d y}{d x}, \frac{d^2 y}{d x^2}, \frac{d^3 y}{d x^3}, \frac{d^4 y}{d x^4}, \ldots, \frac{d^n y}{d x^n}
\end{aligned}
$

Recommended Video Based on Higher Order Derivatives

Solved Exampled Based on Higher Order Derivatives

Example 1: If $y^2+\log _e\left(\cos ^2 x\right)=y, x \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$, then:
[JEE Main 2020]
1) $y^{\prime \prime}(0)=0$
2) $\left|y^{\prime}(0)\right|+\left|y^{\prime \prime}(0)\right|=1$
3) $\left|y^{\prime \prime}(0)\right|=2$
4) $\left|y^{\prime}(0)\right|+\left|y^{\prime \prime}(0)\right|=3$

Solution:

$
\begin{aligned}
& y^2+\log _e\left(\cos ^2 x\right)=y \\
& y^2+2 \log _e(\cos x)=y \\
& 2 y y^{\prime}-2 \frac{\sin x}{\cos x}=y^{\prime} \\
& 2 y y^{\prime}-2 \tan x=y^{\prime} \\
& \therefore y^{\prime}(0)=0 \\
& 2\left(y^{\prime}\right)^2+2 y y^{\prime \prime}-2 \sec ^2 x=y^{\prime \prime} \\
& \therefore\left|y^{\prime \prime}(0)\right|=2
\end{aligned}
$

Hence, the answer is the option 3.

Example 2: Let $f: S \rightarrow S_{\text {where }} S=(0, \infty)$ be twice differentiable function such that $f(x+1)=x f(x)$. If $g: S \rightarrow R$ be defined as $g(x)=\log _e f(x)$ then the value of $\left|g^{\prime \prime}(5)-g^{\prime \prime}(1)\right|$ is equal to: [JEE Main 2021]
1) $\frac{205}{144}$
2) $\frac{197}{144}$
3) $\frac{187}{144}$
4) $0$

Solution:

$
\begin{aligned}
& \ln f(x+1)=\ln (x f(x)) \\
& \ln f(x+1)=\ln x+\ln f(x) \\
& \Rightarrow \quad g(x+1)=\ln x+g(x) \\
& \Rightarrow \quad g(x+1)-g(x)=\ln x \\
& \Rightarrow \quad g^{\prime \prime}(x+1)-g^{\prime \prime}(x)=-\frac{1}{x^2}
\end{aligned}
$
Put $x=1,2,3,4$
$
\begin{aligned}
& g^{\prime \prime}(2)-g^{\prime \prime}(1)=-\frac{1}{1^2} \quad \ldots(1) \\
& g^{\prime \prime}(3)-g^{\prime \prime}(2)=-\frac{1}{2^2} \quad \ldots(2) \\
& g^{\prime \prime}(4)-g^{\prime \prime}(3)=-\frac{1}{3^2} \quad \ldots(3) \\
& g^{\prime \prime}(5)-g^{\prime \prime}(4)=-\frac{1}{4^2} \quad \ldots(4)
\end{aligned}
$
Add all the equations we get

$
\begin{aligned}
& g^{\prime \prime}(5)-g^{\prime \prime}(1)=-\frac{1}{1^2}-\frac{1}{2^2}-\frac{1}{3^2}-\frac{1}{4^2} \\
& \left|g^{\prime \prime}(5)-g^{\prime \prime}(1)\right|=\frac{205}{144}
\end{aligned}
$

Hence, the answer is the option 1.

Example 3: If

$
\cos ^{-1}\left(\frac{y}{2}\right)=\log _{\mathrm{e}}\left(\frac{x}{5}\right)^5,|y|<2
$

then?
[JEE Main 2022]
1) $x^2 y^{\prime \prime}+x y^{\prime}-25 y=0$
2) $x^2 y^{\prime \prime}-x y^{\prime}-25 y=0$
3) $x^2 y^{\prime \prime}-x y^{\prime}+25 y=0$
4) $x^2 y^{\prime \prime}+x y^{\prime}+25 y=0$

Solution:

$
\begin{aligned}
& \cos ^{-1} \frac{\mathrm{y}}{2}=5 \log _{\mathrm{e}} \frac{\mathrm{x}}{5} \\
& \Rightarrow \frac{\mathrm{y}}{2}=\cos \left(5 \log _{\mathrm{e}} \frac{\mathrm{x}}{5}\right) \\
& \Rightarrow \mathrm{y}^{\prime}=-2 \sin \left(5 \log _{\frac{\mathrm{x}}{5}}^5\right) \times \frac{5}{\mathrm{x} / 5} \times \frac{1}{5} \\
& =\frac{-10 \sin \left(5 \log _{\mathrm{e}} \frac{\mathrm{x}}{5}\right)}{\mathrm{x}}
\end{aligned}
$

$\begin{aligned} & \Rightarrow y^{\prime \prime}=\frac{-x \times 10 \cos \left(5 \log _e \frac{x}{5}\right) \times \frac{5}{x / 5} \times \frac{1}{5}+10 \sin \left(5 \log _e \frac{x}{5}\right)}{x^2} \\ & \Rightarrow x^2 y^{\prime \prime}=-50 \cos \left(5 \log _e \frac{x}{5}\right)+10 \sin \left(5 \log _e \frac{x}{5}\right) \\ & \Rightarrow x^2 y^{\prime \prime}=-25 y-x y^{\prime} \\ & \Rightarrow x^2 y^{\prime \prime}+x y^{\prime}+25 y=0\end{aligned}$ṁ

Hence the answer is the option (4).

Example 4:

Let $x=\cos \theta$ and $y=\sin \theta$, then $\frac{d^2 y}{d x^2}=$
1) $\operatorname{cosec}^3 \theta$
2) $-\operatorname{cosec}^3 \theta
$

3) $
\sin ^3 \theta
$

4) $
-\sin ^3 \theta
$

Solution:

Second-order derivative for parametric function-
When we find

$
\begin{aligned}
& \frac{d y}{d x}=F(t) \text { then } \frac{d^2 y}{d x^2}=\frac{\frac{d}{d t} F(t)}{\frac{d x}{d t}} \\
& \frac{d y}{d x}=\frac{\frac{d y}{d \theta}}{\frac{d x}{d \theta}}=\frac{\frac{d}{d \theta} \sin \theta}{\frac{d}{d \theta} \cos \theta}=\frac{\cos \theta}{-\sin \theta}=-\cot \theta \\
& \frac{d^2 y}{d x^2}=\frac{d}{d x}\left(\frac{d y}{d x}\right)=\frac{\frac{d}{d \theta}(-\cot \theta)}{\frac{d x}{d \theta}}=\frac{\operatorname{cosec}^2 \theta}{-\sin \theta}=-\operatorname{cosec}^3 \theta
\end{aligned}
$

Hence, the answer is the option 2.

Example 5:

Let $x=(\theta+\cos \theta)$ and $y=(\theta-\sin \theta)$, then $\frac{d^2 y}{d x^2}$ equals
1) $
\frac{\sin \theta+\cos \theta+1}{(1-\sin \theta)^3}
$

2) $
\frac{\sin \theta-\cos \theta+1}{(1-\sin \theta)^3}
$

3) $
\frac{\sin \theta-\cos \theta-1}{(1-\sin \theta)^3}
$

4) $
\frac{\sin \theta+\cos \theta-1}{(1-\sin \theta)^3}
$

Solution:

$
\begin{aligned}
& \frac{d y}{d x}=\frac{\frac{d y}{d \theta}}{\frac{d x}{d \theta}}=\frac{\frac{d}{d \theta}(\theta-\sin \theta)}{\frac{d}{d \theta}(\theta+\cos \theta)}=\frac{1-\cos \theta}{1-\sin \theta} \\
& \frac{d^2 y}{d x^2}=\frac{d}{d x}\left(\frac{1-\cos \theta}{1-\sin \theta}\right)=\frac{\frac{d}{d \theta}\left(\frac{1-\cos \theta}{1-\sin \theta}\right)}{\frac{d x}{d \theta}} \\
& \frac{d^2 y}{d x^2}=\frac{(1-\sin \theta)(\sin \theta)-(1-\cos \theta)(-\cos \theta)}{(1-\sin \theta)^3}=\frac{\sin \theta+\cos \theta-1}{(1-\sin \theta)^3}
\end{aligned}
$

Hence, the answer is the option 4.

Summary

Higher-order derivative of a Function is an important concept in Calculus. It provides a deep understanding of how the functions interact and change. It is very helpful in practical applications for physics, economics, etc. The chain rule is used to find the derivative of a function with respect to another. The derivative can be found a lot of times like the second, third, and fourth derivative.