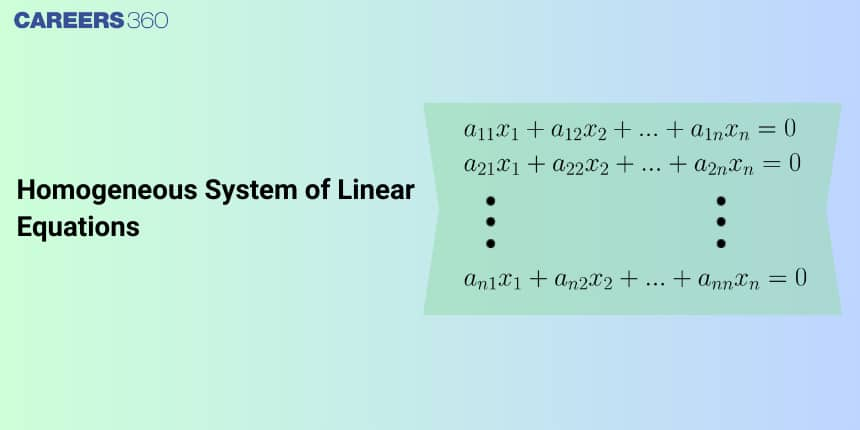
Homogeneous System of Linear Equations

In the homogeneous system of linear equations, the constant term in every equation is equal to 0 . i.e., no equation in such systems has a constant term in it. A homogeneous linear system may have one or infinitely many solutions. But it has at least one solution always. In real life, we use a Homogenous system of linear equations to solve the system of linear equations which helps us to solve age-related problems and time related problems.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. System of Linear Equation
2. Homogenous System of Linear EquationA linear equation with a constant value of zero is called a homogeneous equation.$\\\mathrm{Let,} \\\mathrm{a_1x+b_1y +c_1z=0\;\;\; ...(i)} \\\mathrm{a_2x+b_2y +c_2z=0\;\;\; ...(ii)} \\\mathrm{a_3x+b_3y +c_3z=0\;\;\; ...(iii)} \\\mathrm{be \; three\; homogeneous\; equations} \\\\\mathrm{and \; let\; \Delta = \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}}$
3. Non Homogenous System of Linear Equations
4. Solved Examples Based on Homogenous System of Linear Equations

In this article, we will cover the concept of a Homogenous system of linear equations. This category falls under the broader category of Matrices, which is a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Questions based on this topic have been asked frequently in JEE Mains

System of Linear Equation

A system of linear equations are group of $n$ linear equations containing $n$ number of variables.

1. System of 2 Linear Equations:

It is a pair of linear equations in two variables. It is usually of the form

$a_1x +b_1y + c_1 = 0$

$a_2x +b_2y + c_2 = 0$

Finding a solution for this system means finding the values of $x$ and $y$ that satisfy both equations.

2. System of 3 Linear Equations:

It is a group of 3 linear equations in three variables. It is usually of the form

$a_1x +b_1y + +c_1z + d_1 = 0$

$a_2x +b_2y + +c_2z + d_2 = 0$

$a_3x +b_3y + +c_3z + d_3 = 0$

Finding a solution for this system means finding the values of $x, y$, and $z$ that satisfy all three equations.

Homogenous System of Linear Equation
A linear equation with a constant value of zero is called a homogeneous equation.$\\\mathrm{Let,} \\\mathrm{a_1x+b_1y +c_1z=0\;\;\; ...(i)} \\\mathrm{a_2x+b_2y +c_2z=0\;\;\; ...(ii)} \\\mathrm{a_3x+b_3y +c_3z=0\;\;\; ...(iii)} \\\mathrm{be \; three\; homogeneous\; equations} \\\\\mathrm{and \; let\; \Delta = \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}}$

Note that $x=y=z=0$ will always satisfy this system of equations. So system of homogeneous equations will always have at least one solution.

Also, the solution $x=0, y=0$, and $z=0$ is called a trivial solution, and other solutions are called non-trivial solutions.

• If $\Delta \neq 0$, then $x=0, y=0, z=0$ is the only solution of the above system. This solution is also known as a trivial solution.
• If $\Delta=0$, at least one of $x, y$, and $z$ are non-zero. In this case, we will have non-trivial solutions as well. Also, there would be infinite solutions of such a system of equations.

$\\\mathrm{Let,} \\\mathrm{a_1x+b_1y +c_1z=0\;\;\; ...(i)} \\\mathrm{a_2x+b_2y +c_2z=0\;\;\; ...(ii)} \\\mathrm{a_3x+b_3y +c_3z=0\;\;\; ...(iii)} \\\mathrm{be \; three\; homogeneous\; equation} \\\mathrm{and \; let\; \Delta = \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}}$

If $\Delta\neq 0$, then $x=0, y=0, z=0$ is the only solution of the above system. This solution is also known as a trivial solution.

If $\Delta=0$, at least one of $x, y$ and $z$ are non-zero. This solution is called a non-trivial solution.

Explanation: using equation (ii) and (iii), we have$\\\mathrm{\frac{x}{b_2c_3-b_3c_2} = \frac{y}{c_2a_3-c_3a_2}=\frac{z}{a_2b_3-a_3b_2}} \\\\\mathrm{or \;\; \frac{x}{\begin{vmatrix} b_2 &c_2 \\ b_3 & c_3 \end{vmatrix}}=\frac{y}{\begin{vmatrix} c_2 &a_2 \\ c_3 & a_3 \end{vmatrix}} = \frac{z}{\begin{vmatrix} a_2 & b_2\\ a_3 & b_3 \end{vmatrix}} = k (say \neq 0)} \\\mathrm{\therefore x = k\begin{vmatrix} b_2 &c_2 \\ b_3 & c_3 \end{vmatrix}, y = k\begin{vmatrix} c_2& a_2\\ c_3 & a_3 \end{vmatrix} \; and \; z = k\begin{vmatrix} a_2 & b_2\\ a_3 & b_3 \end{vmatrix}} \\\mathrm{putting\; these\; value\; in \; equation \; (i), we\; have} \\\mathrm{a_1\left \{ k\begin{vmatrix} b_2 & c_2\\ b_3 & c_3 \end{vmatrix} \right \}+b_1\left \{ k\begin{vmatrix} c_2 & a_2\\ c_3 & a_3 \end{vmatrix} \right \}+c_1\left \{ \begin{vmatrix} a_2 & b_2\\ a_3 & b_3 \end{vmatrix} \right \}=0}$

$\\\mathrm{\Rightarrow a_1\begin{vmatrix} b_2 &c_2 \\ b_3 & c_2 \end{vmatrix}-b_1\begin{vmatrix} a_2 & c_2\\ a_3 &c_3 \end{vmatrix}+c_1\begin{vmatrix} a_2 &b_2 \\ a_3 &b_3 \end{vmatrix} = 0 \;\;\;[\because \; k \neq 0]} \\\mathrm{or \;\; \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix} = 0 \; or \; \Delta = 0}$

This is the condition for a system to have a Non-trivial solution.

Non Homogenous System of Linear Equations

A linear equation with a constant value not equal to zero is called a homogeneous equation.

Characteristics of non Homogenous Linear Equations

• If $|\mathrm{A}| \neq 0$, then the system of equations is consistent and has a unique solution $X=A^{-1} B$
• If $|A|=0$ and $(\operatorname{adj} A) \cdot B \neq 0$, then the system of equations is inconsistent and has no solution.
• If $|A|=0$ and $(\operatorname{adj} A) \cdot B=0$, then the system of equations is consistent and has an infinite number of solutions.

Summary

A homogenous system of equations helps us to characterize the equation and also tells us about the solution of linear equations. A system of linear equations helps us to solve time and age-based problems.

Recommended Video :

Solved Examples Based on Homogenous System of Linear Equations

Example 1:

Solution

For non-trivial solution $\Delta = 0$

$\Rightarrow \begin{vmatrix} 1+\cos ^{2}\theta& \sin ^{2}\theta &4\sin 3\theta \\ \cos ^{2}\theta&1+\sin ^{2}\theta &4\sin 3\theta \\ \cos ^{2}\theta&\sin ^{2}\theta & 1+4\sin 3\theta \end{vmatrix}= 0$

$R_{3}\rightarrow R_{3}-R_{2},R_{2}\rightarrow R_{2}-R_{1}$

$\Rightarrow \begin{vmatrix} 1+\cos ^{2}\theta& \sin ^{2} \theta&4\sin 3\theta \\ -1& 1&0 \\ 0 & -1 & 1 \end{vmatrix}= 0$
$\Rightarrow \left ( 1+\cos ^{2}\theta \right )-\sin ^{2} \theta\left ( -1 \right )+4\sin 3\theta= 0$

$\Rightarrow 2+4 \sin 3\theta= 0$
$\Rightarrow \sin 3\theta= \frac{-1}{2}$
$\Rightarrow 3\theta= \frac{7\pi}{6},\frac{11\pi}{6}$
$\Rightarrow \theta= \frac{7\pi}{18},\frac{11\pi}{18}$
$But\: \frac{11\pi}{18}\not\in\left ( 0,\frac{\pi}{2} \right )$

$\Rightarrow \theta= \frac{7\pi}{18}$

Example 2 :

Solution

$\alpha +\beta +\gamma =2\pi$

$\\ \Delta =\begin{vmatrix} 1 & \cos\gamma &\cos \beta \\ \cos\gamma & 1 & \cos \alpha \\ \cos\beta & \cos \alpha & 1 \end{vmatrix}\\$

$=1+2\cos\alpha \cos\beta \cos\gamma -\cos^{2}\beta -\cos^{2}\alpha -\cos^{2}\gamma \\$

$Let \; \gamma =2\pi-\alpha -\beta \\$

$\Rightarrow \Delta =1+2\cos\alpha \cos\beta \cos\left ( \alpha +\beta \right )-\cos^{2}\left ( \alpha +\beta \right )\\$

$=1+2\cos\alpha \cos\beta \left [ \cos\alpha \cos\beta -\sin\alpha \sin\beta \right ]-\cos^{2}\alpha -\cos^{2}\beta\\$

$-\left [ \cos\alpha \cos\beta -\sin\alpha \sin\alpha \right ]^{2}\\$

$=1+2\cos^{2}\alpha \cos^{2}\beta -2\sin\alpha \sin\beta \cos\alpha \cos\beta -\cos^{2}\alpha -\cos^{2}\beta \\$

$-\cos^{2}\alpha \cos^{2}\beta -\sin^{2}\alpha \sin^{\beta }+2\sin\alpha \sin\beta \cos\alpha \cos\beta \\$

$= 1-\cos^{}\alpha -\cos^{\beta }+\cos^{2}\alpha \cos^{2}\beta -\sin^{2}\alpha \sin^{2}\beta \\$

$=\left ( 1-\cos^{2}\alpha \right )\left ( 1-\cos^{2}\beta \right )-\sin^{2}\alpha \sin^{}\beta \\$

$=\sin^{2}\alpha \sin^{2}\beta -\sin^{2}\alpha \sin^{2}\beta=0$

Example 3: