Have you ever noticed how quantities like speed, temperature, or distance change every moment in real life? Understanding these continuous changes is the foundation of calculus, and this is where Limits and Derivatives come into play. In Class 11 Mathematics, a limit describes the value that a function approaches as the input gets closer to a particular number, while a derivative measures the rate at which one quantity changes with respect to another. For example, the derivative of distance with respect to time gives speed, which is a common real-life application seen while driving a car.
Search Colleges, Exams, Schools & more
Login
Limits and Derivatives
This Story also Contains
- Limits And Derivatives in Mathematics
- Left-Hand and Right-Hand Limits – Class 11 Limits and Derivatives
- Derivatives
- Limits and Derivative Class 11 Formulas
- Limits And Derivatives in Mathematics: Solved Previous Year Questions
- List of Topics related to Limits and Derivatives according to NCERT/JEE Mains
- Limits and Derivatives in Different Exams
- Important Books and Resources for Limits and Derivatives
- NCERT Resources for Limits and Derivatives
- NCERT Subjectwise Resources
- Practice Questions based on Limits and Derivatives
- Conclusion
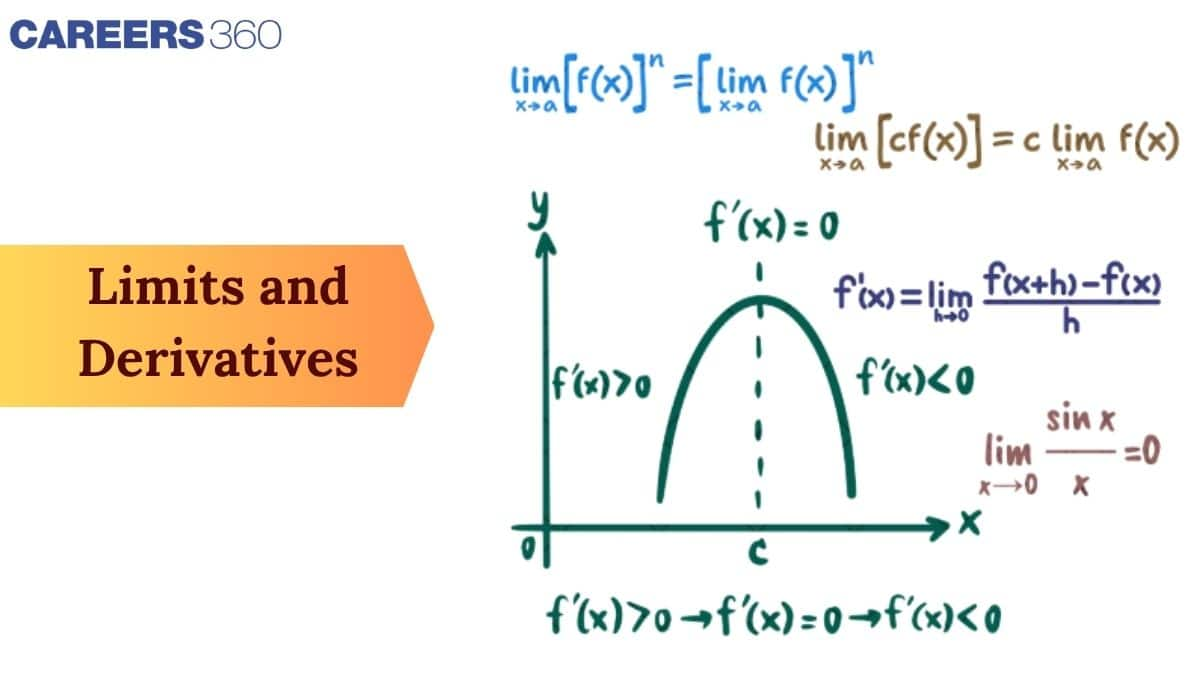
Limits and derivatives have wide real-life applications. They are used in physics to study motion and velocity, in economics to analyse growth and profit, and in engineering to understand change and optimisation. This chapter also acts as a stepping stone for advanced topics like continuity, differentiation, and integration in higher classes. In this article, you will learn Class 11 Limits and Derivatives in a clear and simple manner, including important definitions, formulas, solved examples, and practice questions. The explanations are designed to help you build strong conceptual understanding and prepare confidently for school exams and competitive examinations.
Limits And Derivatives in Mathematics
Limits and Derivatives in Mathematics help us study how quantities change and behave near a given point. This chapter forms the foundation of calculus and is essential for understanding motion, growth, and many advanced mathematical concepts.
What is a Limit?
A limit describes the value that a function approaches as the input gets closer to a specific point. Even if the function is not defined at that point, the limit can still exist by observing the behaviour near it.
Mathematically, the limit of a function $f(x)$ as $x$ approaches $a$ is written as:
$\lim_{x \to a} f(x) = L$
This means that as $x$ gets closer to $a$, the value of $f(x)$ approaches $L$.
Example:
Consider the function $f(x) = x^2$.
-
As $x$ approaches $0$, $f(x)$ approaches $0$.
So, $\lim_{x \to 0} x^2 = 0$.
-
As $x$ approaches $2$, $f(x)$ approaches $4$.
So, $\lim_{x \to 2} x^2 = 4$.
Thus, in general, if $x$ approaches $a$, then $f(x)$ approaches some value $l$:
$\lim_{x \to a} f(x) = l$
Even if the function does not exist at $x = a$, still the limit can exist at that point, as the limit is concerned only about the points close to $x=a$ and not at $x=a$ itself.
Properties of Limits
The following properties are used frequently while solving problems in the limits and derivatives class 11:
-
Limit of a constant
If $c$ is a constant, then $\lim_{x \to a} c = c$
The limit of a constant is the constant itself. -
Limit of the identity function
$\lim_{x \to a} x = a$
As $x$ approaches $a$, the value of $x$ itself approaches $a$. -
Sum of limits
$\lim_{x \to a} [f(x) + g(x)] = \lim_{x \to a} f(x) + \lim_{x \to a} g(x)$
The limit of the sum is the sum of the limits. -
Difference of limits
$\lim_{x \to a} [f(x) - g(x)] = \lim_{x \to a} f(x) - \lim_{x \to a} g(x)$
The limit of the difference is the difference of the limits. -
Constant multiple of a limit
$\lim_{x \to a} [c \cdot f(x)] = c \cdot \lim_{x \to a} f(x)$
A constant factor can be pulled out of the limit. -
Product of limits
$\lim_{x \to a} [f(x) \cdot g(x)] = \lim_{x \to a} f(x) \cdot \lim_{x \to a} g(x)$
The limit of a product is the product of the limits. -
Quotient of limits
If $\lim_{x \to a} g(x) \neq 0$, then
$\lim_{x \to a} \frac{f(x)}{g(x)} = \frac{\lim_{x \to a} f(x)}{\lim_{x \to a} g(x)}$
The limit of a quotient is the quotient of the limits. -
Power of a limit
If $n$ is a positive integer,
$\lim_{x \to a} [f(x)]^n = [\lim_{x \to a} f(x)]^n$
The limit of a function raised to a power is the power of the limit. -
Root of a limit
If $n$ is a positive integer and the limit is defined,
$\lim_{x \to a} \sqrt[n]{f(x)} = \sqrt[n]{\lim_{x \to a} f(x)}$
The limit of a root is the root of the limit. -
Polynomial and rational functions
Limits of polynomial and rational functions can be evaluated by direct substitution if the function is defined at that point.
JEE Main Highest Scoring Chapters & Topics
Focus on high-weightage topics with this eBook and prepare smarter. Gain accuracy, speed, and a better chance at scoring higher.
Download E-bookLeft-Hand and Right-Hand Limits – Class 11 Limits and Derivatives
When learning limits and derivatives in class 11, it’s important to know how a function behaves when the input gets close to a particular value from different directions. This is where left-hand limits and right-hand limits are used. They help us understand the behaviour of functions as the variable approaches a point from either smaller or larger values.
Left-Hand Limit (LHL)
The left-hand limit, written as $ \lim_{x \to a^{-}} f(x) $, describes how the function $f(x)$ behaves when $x$ gets closer to $a$ from values smaller than $a$. In other words, we are observing what happens to the function when $x$ approaches $a$ from the left side of the number line.
For example, if we write $ \lim_{x \to a^{-}} f(x) = LHL $, it means that as $x$ gets closer to $a$ from the left side, the value of $f(x)$ approaches $LHL$.
Right-Hand Limit (RHL)
The right-hand limit, written as $ \lim_{x \to a^{+}} f(x) $, describes how the function $f(x)$ behaves when $x$ approaches $a$ from values greater than $a$. This helps us study the behaviour of the function from the right side of $a$.
If we write $ \lim_{x \to a^{+}} f(x) = RHL $, it means that as $x$ gets closer to $a$ from the right side, the value of $f(x)$ approaches $RHL$.
Example: Let’s understand this with an example, often seen in class 11 maths, limits and derivatives miscellaneous exercise.
Consider the function $ f(x) = \frac{|x|}{x} $. We want to find how this function behaves near $x = 0$ by calculating both the left-hand limit and the right-hand limit.
Left-Hand Limit
We calculate the left-hand limit as:
$ LHL = \lim_{x \to 0^{-}} \frac{|x|}{x} $
Since $x$ is slightly less than $0$, we can write $x = 0 - h$, where $h > 0$ and is very small.
Therefore,
$ = \lim_{h \to 0^{+}} \frac{|0 - h|}{0 - h} $
$ = \lim_{h \to 0^{+}} \frac{h}{-h} $
$ = -1 $
So, the left-hand limit at $x = 0$ is $-1$.
Right-Hand Limit
Now, we calculate the right-hand limit as:
$ RHL = \lim_{x \to 0^{+}} \frac{|x|}{x} $
Since $x$ is slightly greater than $0$, we write $x = 0 + h$, where $h > 0$ and very small:
$ = \lim_{h \to 0^{+}} \frac{|0 + h|}{0 + h} $
$ = \lim_{h \to 0^{+}} \frac{h}{h} $
$ = 1 $
So, the right-hand limit at $x = 0$ is $1$.
Existence of a Limit – Class 11 Limits and Derivatives
From the above example, we see that the left-hand limit is $-1$ and the right-hand limit is $1$. Since they are not equal, the limit at $x = 0$ does not exist.
In general, the limit of a function at $x = a$ exists only if the left-hand limit and right-hand limit are equal. That is, $ \lim_{x \to a^{-}} f(x) = \lim_{x \to a^{+}} f(x) $.
Even if the function is not defined at $x = a$, the limit can still exist if the values from the left and right sides approach the same number. This concept is very useful in class 11 maths limits and derivatives, as it helps us analyse functions at points where they may not be defined but behave consistently near that point.
Derivatives
In real life, we often need to know how quickly something is changing. For example, if you are driving, you may want to know how fast your speed is increasing at a particular moment. This rate of change is what we find using derivatives in class 11, limits and derivatives. The derivative helps us understand how a function changes at any point and is widely used in science, engineering, and economics.
What is a Derivative?
The derivative of a function gives the rate at which the function’s value changes as the input changes. Suppose a function $f$ is defined on an interval that contains a point $x_0$, and the following limit exists:
$ \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} $
Then, the function is said to be differentiable at $x_0$, and the derivative of $f$ at $x_0$ is written as $f^{\prime}(x_0)$ and is defined by:
$ f^{\prime}(x_0) = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} $
This means that the derivative measures how $y$ (which is $f(x)$) changes when $x$ is changed by a small amount $ \Delta x $.
Derivative at All Points
For all values of $x$ where this limit exists, the derivative is written as:
$ f^{\prime}(x) = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} $
This means that the derivative is itself a function of $x$, telling us how $f(x)$ changes at any point.
Notations of Derivatives
There are several common ways to denote the derivative of $y = f(x)$. Some of the widely used notations in class 11 maths limits and derivatives include:
- $f^{\prime}(x)$
- $\frac{dy}{dx}$
- $y^{\prime}$
- $\frac{d}{dx}[f(x)]$
- $D_x[y]$
- $Dy$
- $y_1$
Here, the symbols $\frac{d}{dx}$ or $D$ represent the differential operator, which is used to calculate derivatives.
Limits and Derivative Class 11 Formulas
Operation on Limits
The operations on limits include sum, difference, constant multiplication, product, quotient, power and composition of functions.
Sum law for limits : $\lim\limits _{x \rightarrow a}(f(x)+g(x))=\lim\limits _{x \rightarrow a} f(x)+\lim\limits _{x \rightarrow a} g(x)=L+M$
Difference law for limits : $\lim\limits _{x \rightarrow a}(f(x)-g(x))=\lim\limits _{x \rightarrow a} f(x)-\lim\limits _{x \rightarrow a} g(x)=L-M$
Constant multiple law for limits : $\lim\limits _{x \rightarrow a} c f(x)=c \cdot \lim\limits _{x \rightarrow a} f(x)=c L$
Product law for limits : $\lim\limits _{x \rightarrow a}(f(x) \cdot g(x))=\lim\limits _{x \rightarrow a} f(x) \cdot \lim\limits _{x \rightarrow a} g(x)=L \cdot M$
Quotient law for limits : $\lim\limits _{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim\limits _{x \rightarrow a} f(x)}{\lim\limits _{x \rightarrow a} g(x)}=\frac{L}{M}$ for $M \neq 0$
Power law for limits : $\lim\limits _{x \rightarrow a}(f(x))^n=\left(\lim\limits _{x \rightarrow a} f(x)\right)^n=L^n$ for every positive integer $n$
Composition law of limit: $\lim\limits _{x \rightarrow a}(f \circ g)(x)=f\left(\lim\limits _{x \rightarrow a} g(x)\right)=f(M)$, only if $\mathrm{f}(\mathrm{x})$ is continuous at $\mathrm{g}(\mathrm{x})=\mathrm{M}$.
If $\lim\limits _{x \rightarrow a} f(x)=+\infty$ or $-\infty$, then $\lim\limits _{x \rightarrow a} \frac{1}{f(x)}=0$
Indeterminate Forms
Indeterminate forms arise in limits when the standard limit rules yield expressions that do not directly lead to a specific value. If we directly substitute $x = a$ in $f(x)$ while evaluating $\lim\limits _{x \rightarrow a} f(x)$ and will get one of the seven following forms $\frac{0}{0}, \frac{\infty}{\infty}, \infty-\infty, 1^{\infty}, 0^0, \infty^0, \infty \times 0$ then it is called indeterminate form.
Example: $\lim\limits _{x \rightarrow 2} \frac{x^2-4}{x-2}=\frac{0}{0}$ indeterminate form.
L'Hospital's Rule
L'Hospital's Rule states that, if $\lim\limits _{x \rightarrow a} \frac{f(x)}{g(x)}$ is of $\frac{0}{0}$ or $\frac{\infty}{\infty}$ form, then differentiate numerator and denominator till this intermediate form is removed. $\lim\limits _{x \rightarrow a} \frac{f(x)}{g(x)}=\lim\limits _{x \rightarrow a} \frac{f^{\prime}(x)}{g^{\prime}(x)}$
But, if we again get the indeterminate form $\frac{0}{0}$ or $\frac{\infty}{\infty} \lim\limits _{x \rightarrow a} \frac{f(x)}{g(x)}=\lim\limits _{x \rightarrow a} \frac{f^{\prime}(x)}{g^{\prime}(x)}=\lim\limits _{x \rightarrow a} \frac{f^{\prime \prime}(x)}{g^{\prime \prime}(x)}$ (so we differentiate numerator and denominator again)
This process is continued till the indeterminate form $\frac{0}{0}$ or $\frac{\infty}{\infty}$ is removed.
Example:
Evaluate $\lim\limits _{x \rightarrow 0} \frac{\sin x}{x}$
$
\lim\limits _{x \rightarrow 0} \frac{\sin x}{x}= \frac{0}{0}
$
But by L'Hospital rule, $\lim\limits _{x \rightarrow 0} \frac{\sin x}{x}=\lim\limits _{x \rightarrow 0} \frac{\cos x}{1}=1$
Derivatives of Some Basic Functions
The differentiation of some basic functions are:
1. $\frac{d}{d x}($ constant $)=0$
2. $\frac{d}{d x}\left(\mathbf{x}^{\mathbf{n}}\right)=\mathbf{n} \mathbf{x}^{\mathbf{n}-1}$
3. $\frac{d}{d x}\left(\mathbf{a}^{\mathrm{x}}\right)=\mathbf{a}^{\mathrm{x}} \log _{\mathrm{e}} \mathbf{a}$
4. $\quad \frac{d}{d x}\left(\mathrm{e}^{\mathrm{x}}\right)=\mathrm{e}^{\mathrm{x}} \log _{\mathrm{e}} \mathrm{e}=\mathrm{e}^{\mathrm{x}}$
5. $\frac{d}{d x}\left(\log _{\mathrm{e}}|\mathbf{x}|\right)=\frac{\mathbf{1}}{\mathbf{x}}, \quad \mathbf{x} \neq 0$
6. $\quad \frac{d}{d x}\left(\log _{\mathbf{a}}|\mathbf{x}|\right)=\frac{1}{\mathbf{x} \log _{\mathrm{e}} \mathbf{a}}, \quad \mathbf{x} \neq 0$
7. $\frac{d}{d x}(\sin (\mathbf{x}))=\cos (\mathbf{x})$
8. $\frac{d}{d x}(\cos (\mathbf{x}))=-\sin (\mathbf{x})$
9. $\frac{d}{d x}(\tan (\mathbf{x}))=\sec ^2(\mathbf{x})$
10. $\frac{d}{d x}(\cot (\mathbf{x}))=-\csc ^2(\mathbf{x})$
11. $\frac{d}{d x}(\sec (\mathbf{x}))=\sec (\mathbf{x}) \tan (\mathbf{x})$
12. $\frac{d}{d x}(\csc (\mathbf{x}))=-\csc (\mathbf{x}) \cot (\mathbf{x})$
Rules of Differentiation
The important rules of differentiation are
- Power Rule
- Sum and Difference Rule
- Product Rule
- Quotient Rule
- Chain Rule
Let $f(x)$ and $g(x)$ be differentiable functions and $k$ be a constant. Then each of the following rules holds
Sum Rule
The derivative of the sum of a function $f$ and a function $g$ is the same as the sum of the derivative of $f$ and the derivative of $g$.
$
\frac{d}{d x}(f(x)+g(x))=\frac{d}{d x}(f(x))+\frac{d}{d x}(g(x))
$
In general,
$
\frac{d}{d x}(f(x)+g(x)+h(x)+\ldots \ldots)=\frac{d}{d x}(f(x))+\frac{d}{d x}(g(x))+\frac{d}{d x}(h(x))+\ldots \ldots
$
Difference Rule
The derivative of the difference of a function $f$ and $a$ function $g$ is the same as the difference of the derivative of $f$ and the derivative of $g$.
$
\begin{aligned}
& \frac{d}{d x}(f(x)-g(x))=\frac{d}{d x}(f(x))-\frac{d}{d x}(g(x)) \\
& \frac{d}{d x}(f(x)-g(x)-h(x)-\ldots \ldots)=\frac{d}{d x}(f(x))-\frac{d}{d x}(g(x))-\frac{d}{d x}(h(x))-\ldots \ldots
\end{aligned}
$
Constant Multiple Rule
The derivative of a constant $k$ multiplied by a function $f$ is the same as the constant multiplied by the derivative of $f$
$
\frac{d}{d x}(k f(x))=k \frac{d}{d x}(f(x))
$
Product rule
Let $f(x)$ and $g(x)$ be differentiable functions. Then,
$
\frac{d}{d x}(f(x) g(x))=g(x) \cdot \frac{d}{d x}(f(x))+f(x) \cdot \frac{d}{d x}(g(x))
$
This means that the derivative of a product of two functions is the derivative of the first function times the second function plus the derivative of the second function times the first function.
Extending the Product Rule
If three functions are involved, i.e let $k(x)=f(x) \cdot g(x) \cdot h(x)$
Let us have a function $\mathrm{k}(\mathrm{x})$ as the product of the function $\mathrm{f}(\mathrm{x}), \mathrm{g}(\mathrm{x})$ and $\mathrm{h}(\mathrm{x})$. That is, $k(x)=(f(x) \cdot g(x)) \cdot h(x)$. Thus,
$
k^{\prime}(x)=\frac{d}{d x}(f(x) g(x)) \cdot h(x)+\frac{d}{d x}(h(x)) \cdot(f(x) g(x))
$
[By applying the product rule to the product of $f(x) g(x)$ and $h(x)$.]
$
\begin{aligned}
& =\left(f^{\prime}(x) g(x)+g^{\prime}(x) f(x)\right) h(x)+h^{\prime}(x) f(x) g(x) \\
& =f^{\prime}(x) g(x) h(x)+f(x) g^{\prime}(x) h(x)+f(x) g(x) h^{\prime}(x)
\end{aligned}
$
Quotient Rule
Let $f(x)$ and $g(x)$ be differentiable functions. Then
$
\frac{d}{d x}\left(\frac{f(x)}{g(x)}\right)=\frac{g(x) \cdot \frac{d}{d x}(f(x))-f(x) \cdot \frac{d}{d x}(g(x))}{(g(x))^2}
$
OR
if $h(x)=\frac{f(x)}{g(x)}$, then $h^{\prime}(x)=\frac{f^{\prime}(x) g(x)-g^{\prime}(x) f(x)}{(g(x))^2}$
As we see in the following theorem, the derivative of the quotient is not the quotient of the derivatives.
Chain Rule
If $u(x)$ and $v(x)$ are differentiable functions, then $u o v(x)$ or $u[v(x)]_{\text {is also differentiable. }}$
If $y=u o v(x)=u[v(x)]$, then
$
\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{\mathrm{d} u\{v(x)\}}{\mathrm{d}\{v(x)\}} \times \frac{\mathrm{d}}{\mathrm{d} x} v(x)
$
is known as the chain rule. Or,
$
\text { If } y=f(u) \text { and } u=g(x) \text {, then } \frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{\mathrm{d} y}{\mathrm{~d} u} \cdot \frac{\mathrm{d} u}{\mathrm{~d} x}
$
The chain rule can be extended as follows
If $y=[\operatorname{uovow}(x)]=u[v\{w(x)\}]$, then
$
\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{\mathrm{d}[u[v\{w(x)\}]}{\mathrm{d} v\{w(x)\}} \times \frac{\mathrm{d}[v\{w(x)\}]}{\mathrm{d} w(x)} \times \frac{\mathrm{d}[w(x)]}{\mathrm{d} x}
$
Limits And Derivatives in Mathematics: Solved Previous Year Questions
Question 1:
The value of $\lim _{x \rightarrow \infty} \frac{4(x)^{1 / 4}+5(x)^{1 / 5}+6(x)^{1 / 6}+\ldots .+n(x)^{1 / n}}{(4 x-3)^{1 / 4}+(4 x-3)^{1 / 5}+\ldots+(4 x-3)^{1 / n}}$ is:
Solution:
$\begin{aligned} & \quad \lim _{x \rightarrow \infty} \frac{4(x)^{1 / 4}+5(x)^{1 / 5}+6(x)^{1 / 6}+\ldots .+n(x)^{1 / n}}{(4 x-3)^{1 / 4}+(4 x-3)^{1 / 5}+\ldots+(4 x-3)^{1 / n}} \\ & \text { Put } x=\frac{1}{h}, \text { as } x \rightarrow \infty, h \rightarrow 0 \\ & \lim _{h \rightarrow 0} \frac{4(h)^{-1 / 4}+5(h)^{-1 / 5}+\ldots .+n(h)^{-1 / n}}{h^{-1 / 4}(4-3 h)^{1 / 4}+h^{-1 / 5}(4-3 h)^{1 / 5}+\ldots+h^{-1 / n}(4-3 h)^{1 / n}} \\ & \Rightarrow \quad \lim _{h \rightarrow 0} \frac{4+5(h)^{\left(\frac{1}{4}-\frac{1}{5}\right)}+6(h)^{\left(\frac{1}{4}-\frac{1}{6}\right)}+\ldots .+n(h)^{\left(\frac{1}{4}-\frac{1}{n}\right)}}{(4-3 h)^{1 / 4}+(h)^{\left(\frac{1}{4}-\frac{1}{5}\right)}(4-3 h)^{1 / 5}+\ldots .+h^{\left(\frac{1}{4}-\frac{1}{n}\right)}(4-3 h)^{1 / n}} \\ & \Rightarrow \quad \frac{4+0+0+\ldots .+0}{4^{1 / 4}+0+0+\ldots .+0}=2 \sqrt{2}\end{aligned}$
Hence, the answer is $2 \sqrt 2$.
Question 2:
${ }_{\text {If }} y=\frac{\sin (x+9)}{\cos x}$ then $\frac{d y}{d x}$ at $x=0$ is:
Solution:
$\begin{aligned} & y=\frac{\sin (x+9)}{\cos x} \\ & \frac{d y}{d x}=\frac{\cos x \cos (x+9)-\sin (x+9)(-\sin x)}{\cos ^2 x} \\ & =\frac{\cos x \cos (x+9)+\sin (x+9) \sin x}{\cos ^2 x} \\ & =\frac{\cos (x+9-x)}{\cos ^2 x}=\frac{\cos 9}{\cos ^2 x} \\ & \left(\frac{d y}{d x}\right)_{x=0}=\frac{\cos 9}{(1)^2}=\cos 9\end{aligned}$
Hence, the correct answer is cos 9.
Question 3:
If $y=\sqrt{x}+\frac{1}{x}$, then $\frac{d y}{d x}$ at $\mathrm{x}=1$ is:
Solution:
$\begin{aligned} & y=\sqrt{x}+\frac{1}{x} \\ & \frac{d y}{d x}=\frac{1}{2 \sqrt{x}}-\frac{1}{x^2} \\ & \left(\frac{d y}{d x}\right)_{x=1}=\frac{1}{2}-1=-\frac{1}{2}\end{aligned}$
Hence, the correct answer is 0.
Question 4:
$\lim _{x \rightarrow 0} \frac{(\tan 2 x-x)}{3 x-\sin x}$ is:
Solution:
$\lim _{x \rightarrow 0} \frac{(\tan 2 x-x)}{3 x-\sin x}=\lim _{x \rightarrow 0} \frac{\left(\frac{\tan 2 x}{x}-1\right)}{\left(3-\frac{\sin x}{x}\right)}=\lim _{x \rightarrow 0} \frac{\left(\frac{2 \tan 2 x}{2 x}-1\right)}{\left(3-\frac{\sin x}{x}\right)}=\frac{2-1}{3-1}=\frac{1}{2}$
Hence, the correct answer is $\frac{1}{2}$.
Question 5:
$\lim _{x \rightarrow 0}\left(\frac{\sin x}{\sqrt{x+1}-\sqrt{1-x}}\right)$ is:
Solution:
$\begin{aligned} & \lim _{x \rightarrow 0}\left(\frac{\sin x}{\sqrt{x+1}-\sqrt{1-x}}\right) \\ & =\lim _{x \rightarrow 0}\left(\frac{\sin x(\sqrt{x+1}+\sqrt{1-x})}{(\sqrt{x+1}-\sqrt{1-x})(\sqrt{x+1}+\sqrt{1-x})}\right) \\ & =\lim _{x \rightarrow 0}\left(\frac{\sin x(\sqrt{x+1}+\sqrt{1-x})}{(x+1-1+x)}\right) \\ & =\lim _{x \rightarrow 0}\left(\frac{\sin x(\sqrt{x+1}+\sqrt{1-x})}{2 x}\right) \\ & =1\end{aligned}$
Hence, the correct answer is 1.
List of Topics related to Limits and Derivatives according to NCERT/JEE Mains
This section covers all the important topics from the limits and derivatives class 11 as per the NCERT and JEE Main, helping students focus on key areas for better preparation.
Limits and Derivatives in Different Exams
The chapter on Limits and Derivatives forms the foundation of calculus in Class 11 and Class 12 Mathematics. It is widely tested in board exams and competitive examinations as it introduces the concept of change and continuity. The table below shows the exam-wise focus areas, commonly asked topics, and preparation tips.
| Exam Name | Focus Area | Common Topics Asked | Preparation Tips |
|---|---|---|---|
| CBSE Board | Conceptual clarity & numericals | Limits of functions, basic derivatives, derivative formulas | Learn the NCERT theory and practice all textbook examples |
| JEE Main | Problem-solving & accuracy | Standard limits, derivatives of algebraic and trigonometric functions | Practise MCQs and numerical-based questions regularly |
| JEE Advanced | Analytical thinking | Complex limit problems, derivative-based applications | Solve previous years’ advanced-level questions |
| NEET | Basics & speed | Standard limits, simple differentiation | Focus on the quick application of formulas |
| State Board Exams (ICSE, UP Board, RBSE, etc) | Theory-oriented | Definitions of limits and derivatives, basic problems | Revise textbook concepts and practice solved examples |
| Mathematics Olympiads | Concept application | Challenging limit problems, advanced differentiation | Strengthen fundamentals and practise higher-level questions |
Important Books and Resources for Limits and Derivatives
Here you will find the best books and study materials that explain limits and derivatives clearly and provide practice questions aligned with the class 11 maths limits and derivatives syllabus.
| Book Title | Author / Publisher | Description |
|---|---|---|
| NCERT Class 11 Mathematics | NCERT | Official textbook covering all fundamentals and exercises on limits and derivatives. |
| Mathematics for Class 11 | R.D. Sharma | Detailed explanations, solved examples, and practice problems for limits and derivatives. |
| Objective Mathematics | R.S. Aggarwal | Diverse MCQs and exercises for practice, including calculus basics. |
| Arihant All-In-One Mathematics | Arihant | Comprehensive topic coverage with ample solved and unsolved problems. |
| Calculus Made Easy | M.L. Khanna | Simplified approach to fundamental calculus concepts, including limits and derivatives. |
NCERT Resources for Limits and Derivatives
This part lists the essential NCERT resources for studying limits and derivatives, which form the foundation for understanding concepts and solving problems effectively.
NCERT Subjectwise Resources
In this section, you will get subject-specific NCERT resources that offer detailed explanations, examples, and solved questions related to class 11.
| Subject | NCERT Notes Link | NCERT Solutions Link | NCERT Exemplar Link |
|---|---|---|---|
| Mathematics | NCERT Notes Class 11 Maths | NCERT Solutions for Class 11 Mathematics | NCERT Exemplar Class 11 Maths |
| Physics | NCERT Notes Class 11 Physics | NCERT Solutions for Class 11 Physics | NCERT Exemplar Class 11 Physics |
| Chemistry | NCERT Notes Class 11 Chemistry | NCERT Solutions for Class 11 Chemistry | NCERT Exemplar Class 11 Chemistry |
Practice Questions based on Limits and Derivatives
This section provides practice questions based on limits and derivatives, helping students strengthen their problem-solving skills and prepare for exams like JEE Main.
Conclusion
Limits and Derivatives introduce students to the core ideas of calculus and the study of change. A clear understanding of definitions, formulas, and applications helps in solving problems accurately and builds a strong base for higher mathematics. With regular practice and concept-based learning, students can confidently handle this chapter in school and competitive examinations.
Frequently Asked Questions (FAQs)
Q: What are limits and derivatives class 11?
A:
Limits help us find the value a function approaches near a specific point, while derivatives measure how fast a function’s value is changing at that point.
Q: What are the formulas for limits and derivatives in class 11?
A:
For limits, common formulas include $ \lim_{x \to a} c = c $, $ \lim_{x \to a} x = a $, and trigonometric limits like $ \lim_{x \to 0} \frac{\sin x}{x} = 1 $. The derivative formula is $ f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} $.
Q: How is continuity connected to limits and derivatives?
A:
For a function to be differentiable at a point, it must be continuous there. Continuity ensures that limits exist and derivatives can be calculated.
Q: Can a limit be infinity?
A:
If a limit tends to infinity, then the limit does not exist.
Q: Is $\frac{0}{0}$ defined?
A:
$\frac{0}{0}$ is not defined. It is called a indeterminate value. If a limit tends to indeterminate value
Articles
Upcoming Exams
