Logarithmic Inequalities: Definition, Problems with Solutions

Inequalities are mathematical expressions showing the relationship between two values, indicating that one value is greater than, less than, or not equal to another. Understanding inequalities is crucial for solving various mathematical problems, from basic arithmetic to advanced calculus. Especially, logarithmic inequalities are important in solving log-related inequalities.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Inequalities
2. Logarithmic inequalities
3. Solved Examples Based On the Logarithmic Inequalities

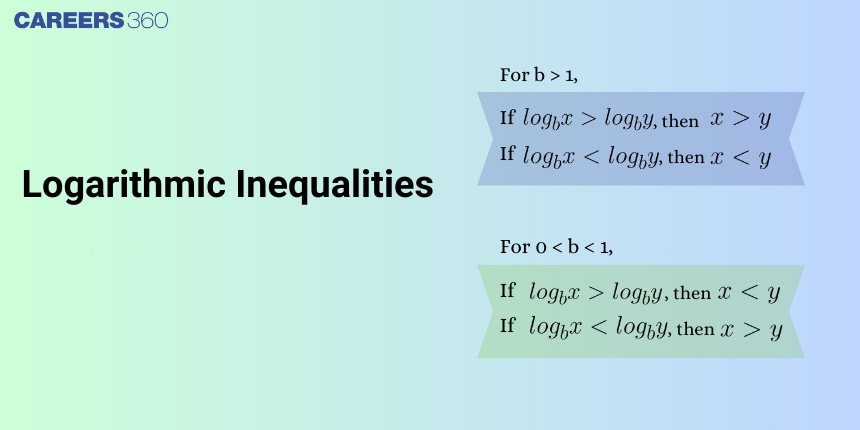
In this article, we will cover the concepts of logarithmic inequalities. This concept falls under the broader category of sets relation and function, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of two questions have been asked on this concept, including two in 2023.

Inequalities

Inequalities are the relationship between two expressions that are not equal to one another. Symbols denoting the inequalities are $<,>, \leq, \geq$, and $\neq$.
- $x<4$, "is read as $x$ less than 4 ", $x \leq 4$, "is read as $x$ less than or equal to 4 ".
- Similarly $x>4$, "is read as $x$ greater than 4 " and $x \geq 4$, "is read as $x$ greater than or equal to $4^{\text {"N }}$.

The process of solving inequalities is the same as of equality but instead of equality symbol inequality symbol is used throughout the process.

Logarithmic inequalities

$\begin{aligned} & \log _a x>\log _a y=\left\{\begin{array}{lc}x>y, & \text { if } a>1 \\ x<y, & \text { if } 0<a<1\end{array}\right. \\ & \log _a x>y= \begin{cases}x>a^y, & \text { if } a>1 \\ x<a^y, & \text { if } 0<a<1\end{cases} \\ & \log _a x<y= \begin{cases}x<a^y, & \text { if } a>1 \\ x>a^y, & \text { if } 0<a<1\end{cases} \end{aligned}$So, we change the sign of inequality while removing log when the base is less than 1

Note: We always take the intersection of the answer of this inequality with the domains of all the log terms involved in the inequality.

Steps for Solving an Equation involving Logarithmic Functions

1. Isolate the logarithmic function.
2. If convenient, express both sides as logs with the same base and equate the arguments of the log functions. Otherwise, rewrite the log equation as an exponential equation.

Recommended Video Based on Logarithmic Inequalities

Solved Examples Based On the Logarithmic Inequalities

Example 1: What is the value of $x$ satisfying the inequality $\log _5(x+5)>\log _7(x+5)$ ?
Solution:
First, we change the base to make the base of both sides the same.

$\begin{aligned}
& \log _b x=\frac{\log _a x}{\log _a b} \\
& \frac{\log (\mathrm{x}+5)}{\log 5}>\frac{\log (\mathrm{x}+5)}{\log 7}
\end{aligned}$

Now for this equation to be true, we observe that

$\begin{aligned}
& \frac{\log (x+5)}{\log 5}>\frac{\log (x+5)}{\log 7} \\
& \frac{\log (x+5)}{\log (5)}-\frac{\log (x+7)}{\log 7}>0 \\
& \log (x+5)>0 \\
& x+5>10^0 \\
& x+5>1 \\
& x>-4
\end{aligned}$

Example 2: The number of distinct solutions of the equation, $\log _{\frac{1}{2}}|\sin x|=2-\log _{\frac{1}{2}}|\cos x|$ in the interval $[0,2 \pi]$, is $\qquad$
Solution:

$\begin{aligned}
& \log _{\frac{1}{2}}(|\sin (x)|)+\log _{\frac{1}{2}}(|\cos (x)|)=2 \\
& \log _{\frac{1}{2}}(|\sin (x)||\cos (x)|)=2 \\
& \log _{\frac{1}{2}}(|\sin (x)||\cos (x)|)=\log _{\frac{1}{2}}\left(\frac{1}{4}\right) \\
& |\sin x||\cos x|=\frac{1}{4} \\
& \sin 2 \theta=\frac{1}{2} \\
& x=\frac{\pi}{12}+\pi n, x=\frac{5 \pi}{12}+\pi n
\end{aligned}$
The total number of solutions is 8

Hence, the answer is 8.

Example 3 Let a complex number $z,|z| \neq 1$, satisfy $\log _{\frac{1}{\sqrt{2}}}\left(\frac{|z|+11}{(|z|-1)^2}\right) \leq 2$ Then, the largest value of $|z|_{\text {is equal to }}$ $\qquad$
Solution:

$\begin{array}{r}
\log _{\frac{1}{\sqrt{2}}}\left(\frac{|z|+11}{(|z|-1)^2}\right) \leq 2 \\
\frac{|z|+11}{(|z|-1)^2} \geq \frac{1}{2} \\
2|z|+22 \geq(|z|-1)^2 \\
2|z|+22 \geq|z|^2+1-2|z| \\
|z|^2-4|z|-21 \leq 0 \\
(|z|-7)(|z|+3) \leq 0 \\
|z| \in[-3,7]
\end{array}$

$\therefore \quad$ Largest value of $|z|$ is 7
Hence, the answer is 7 .

Hence, the answer is 7.

Example 4: The solution set of the inequation $1+\log _{\frac{1}{3}}\left(x^2+x+1\right)>0$ is:
Solution:

$\begin{aligned}
& \text { (i) } \log _{\frac{1}{3}}\left(x+x^2+1\right)>-1 \\
& \Rightarrow x^2+x+1<3 \\
& \Rightarrow x^2+x-2<0 \\
& \Rightarrow(x+2)(x-1)<0 \quad \Rightarrow x \in(-2,1) \\
& \text { and }
\end{aligned}$

(ii) $x^2+x+1>0 \Rightarrow x \in R$. $\qquad$ (ii)
by (i) $\&$ (ii) $x \in(-2,1)$

Example 5: What is the value x when $\log _{\frac{1}{2}}(x-1)>1$
Solution:

$\begin{aligned}
& \log _{0.5}(x-1)>1 \\
& (x-1)<(0.5)^1 \\
& x-1<0.5 \text { and } x-1>0 \\
& 1<x<1.5
\end{aligned}$