Method of Difference

While solving sequence and series problems, we often come across such series that can not be solved using the traditional methods. To solve such types of questions, we use the method of differences. Method of Differences is a trick method to solve those sequence and series questions that can not be solved using traditional methods. In real life, we use the Method of Differences to solve complex series that are neither AP nor GP.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Method of Differences
2. Steps to solve questions using the Method of Differences
3. Method of Differences (Shortcut)
4. Summary
5. Solved Examples Based on the Method of Differences

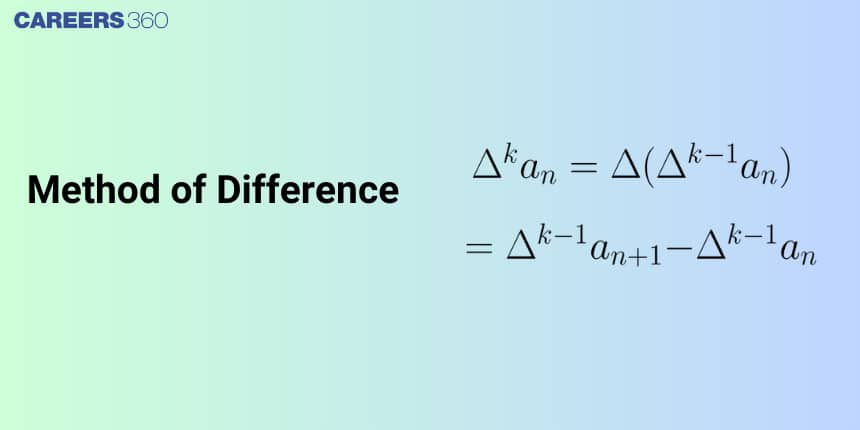
In this article, we will cover the Method of Difference. This category falls under the broader category of sequence and series, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main Exam (from 2013 to 2023), a total of eleven questions have been asked on this concept, including one in 2023.

Method of Differences

The method of differences is a method to solve the sequence and series questions that can not be solved using the concepts of Arithmetic Progression and Geometric Progression. In this method, we try to get the AP or GP series by subtracting the subsequent terms of the series.

Steps to solve questions using the Method of Differences

Following is the step-by-step procedure to calculate a series by using the method of differences :

Step 1: Suppose $a_1, a_2, a_3, \ldots \ldots$ is a sequence such that the sequence is neither an Arithmetic Progression nor a Geometric progression.

Step 2: Find the difference between subsequent terms of the series. We do not subtract the first and last term of the series.

Step 3: Check if $a_2-a_1, a_3-a_3, \ldots$ is either an. A.P. or a G.P.
Step 4: When we successfully determine the nature of the series, we calculate the sum of the series for ( $\mathrm{n}-1$ ) terms.

Step 5: Now, we have a simplified solution of the series.

Method of Differences (Shortcut)

To find the $\mathrm{n}^{\text {th }}$ term of the series, you can use the following steps:
1. If the sequence of the first consecutive difference is in A.P., then the $n^{\text {th }}$ term, $T_n=a n^2+b n+c$ or $a(n-1)(n-2)+b(n-1)+$ $c$, where $\mathrm{a}, \mathrm{b}$, and c are constants. To find the value of $a, b$, and $c$ put $n=1,2,3$ and put the value of $T_1, T_2, T_3$.
2. If the sequence of the first consecutive difference is in G.P., then the $n$th term, $T_n=a r^n+b$, where $a$ and $b$ are constant terms and $r$ is the common ratio of GP. To find the value of a and $b$ put $n=1,2$ and put the value of $T_1, T_2$

Summary

When the consecutive differences of a series are in arithmetic progression (AP) or geometric progression (GP), it means there is a systematic way in which each term changes relative to the previous one. Understanding whether the consecutive term is AP or GP helps us to know the pattern of the series and also enables us to find the general term of the sequence. These progressions provide a framework to understand how each term relates to the next in terms of either constant increments (AP) or multiplicative factors (GP).

Recommended Video :

Solved Examples Based on the Method of Differences

Example 1: Suppose f is a function satisfying $\mathrm{f}(\mathrm{x}+\mathrm{y})=\mathrm{f}(\mathrm{x})+\mathrm{f}(\mathrm{y})$ for all $x, y \in \mathbb{N}$ and $f(1)=\frac{1}{5} \sum_{\text {If }}^{m=1} \frac{f(n)}{n(n+1)(n+2)}=\frac{1}{12}$, then $m$ is equal to
[JEE MAINS 2023]
Solution

$
\mathrm{f}(\mathrm{x}+\mathrm{y})=\mathrm{f}(\mathrm{x})+\mathrm{f}(\mathrm{y}) \forall \mathrm{x}, \mathrm{y} \in \mathrm{N} \text { and } \mathrm{f}(1)=\frac{1}{5}
$

for $x=y=1$

$
\begin{aligned}
& \mathrm{f}(2)=\mathrm{f}(1)+\mathrm{f}(1)=2 \mathrm{f}(1) \\
& \mathrm{f}(3)=\mathrm{f}(2+1)=\mathrm{f}(2)+\mathrm{f}(1)=3 \mathrm{f}(1)
\end{aligned}
$

in General

$
f(n)=n f(1)=\frac{n}{5}
$
$\begin{aligned}
& \sum_{\mathrm{n}=1}^{\mathrm{m}} \frac{\mathrm{f}(\mathrm{n})}{\mathrm{n}(\mathrm{n}+1)(\mathrm{n}+2)}=\frac{1}{12} \\
& \Rightarrow \sum_{\mathrm{n}=1}^{\mathrm{m}} \frac{\mathrm{n}}{5 \mathrm{n}(\mathrm{n}+1)(\mathrm{n}+2)}=\frac{1}{12} \\
& \Rightarrow \frac{1}{5} \sum_{\mathrm{n}=1}^{\mathrm{m}} \frac{1}{(n+1)(n+2)}=\frac{1}{12} \\
& \Rightarrow \sum_{\mathrm{n}=1}^{\mathrm{m}}\left(\frac{1}{\mathrm{n}+1}-\frac{1}{\mathrm{n}+2}\right)=\frac{5}{12} \\
& \Rightarrow\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\ldots \ldots .+\left(\frac{1}{m+1}-\frac{1}{m+2}\right)=\frac{5}{12} \\
& \Rightarrow \frac{1}{2}-\frac{1}{m+2}=\frac{5}{12} \\
& \Rightarrow \frac{1}{\mathrm{~m}+2}=\frac{1}{2}-\frac{5}{12}=\frac{1}{12} \\
& \Rightarrow \mathrm{m}=10
\end{aligned}$

Hence, the answer is the 10.

Example 2: Find the sum of series $1+3+7+13+\ldots+211$

Solution

$
S_n=1+3+7+13+21 \ldots
$
Differences are $2,4,6,8, \ldots$ which is an $A P$
For the difference in A.P., By the above concept

$
T_n=a n^2+b n+c
$

put $n=1,2$, and 3

$
T_n=n^2-n+1
$
For last term 211, $n=15$

$
\begin{aligned}
& S_n=\sum_1^{15} T_n \\
& S_n=\frac{n(n+1)(2 n+1)}{6}-\frac{n(n+1)}{2}+n \\
& S_n=\frac{1}{3}\left(n^3+2 n\right) \\
& S_{15}=1135
\end{aligned}
$

Hence, the answer is 1135

Example 3: Find the sum first 8 terms of the series

$
1+3+7+15+29 \ldots
$

Solution

Now, the given series is

$
1+3+7+15+29 \ldots
$

difference of consecutive terms $=2+4+8+14 \ldots$
difference of this difference $=2+4+6+.$.
This is in A.P.
by above concept

$
T_n=a n^3+b n^2+c n+d
$

Put $n=1,2,3,4$ and solving the equations formed, we get

$
\begin{aligned}
& d=-1, c=8 / 3, b=-1, a=\frac{1}{3} \\
& T_n=\frac{1}{3}\left[n^3-3 n^2+8 n-3\right] \\
& S_n=\sum_1^8 T_n \\
& S_8=148
\end{aligned}
$

Hence, the answer is 148

Example 4: The $10^{th}$ term of the series $2+8+20+40+70+112+\ldots \ldots$.

Solution
The sequence of first consecutive differences is $6,12,20,30,42$.
The sequence of second consecutive differences is $6,8,10,12 \ldots \ldots$ it is an AP

$
\begin{aligned}
& S_n=2+8+20+40+70+112+\ldots \ldots+T_{n-1}+T_n \\
& S_n=2+8+20+40+70+112+\ldots \ldots+T_{n-1}+T_n \\
& 0=2+6+12+20+30+42+\ldots \ldots+\left(T_{n-1}-T_n\right)-T_n \\
& T_n=2+6+12+20+30+42+\ldots \ldots \ldots+\text { upto } n \text { term }
\end{aligned}
$

Or

$
\begin{aligned}
& T_n=2+6+12+20+30+42+\ldots \ldots \ldots+t_{n-1}+t_n \\
& T_n=2+6+12+20+30+42+\ldots \ldots \ldots+t_{n-1}+t_n
\end{aligned}
$

Substract (iii) - (iv)

Hence, the answer is 440

$
\begin{aligned}
& t_n=2+4+6+8+10+12+\ldots \ldots \ldots \ldots\left(t_{n-1}-t_n\right) \\
& t_n=\frac{n}{2}(2 \times 2+(n-1) \times 2)=n^2+n
\end{aligned}
$
Example 5: The sum of 8 terms of series $1+5+13+29 \ldots$. is:

Solution: Differences in consecutive terms are $4,8,16$ $\qquad$ which is a GP with $r=2$

So, let $a_n=a .2^n+c$
Put $\mathrm{n}=1: a_1=a .2+c \Rightarrow 2 a+c=1$
Put $\mathrm{n}=2: a_2=a .2^2+c \Rightarrow 4 a+c=5$
(2) - (1) $: 2 a=4 \Rightarrow a=2$

Using (1) $\Rightarrow c=-3$
So, $a_n=2.2^n-3$

$
\begin{aligned}
\sum a_n & =2 \sum 2^n-3 \sum 1 \\
& =2\left(2+2^2+2^3+\ldots .2^n\right)-3 . n \\
& =2.2 \frac{\left(2^n-1\right)}{(2-1)}-3 n \\
& =4\left(2^n-1\right)-3 n
\end{aligned}
$

So, $S-8=4 .\left(2^8-1\right)-24=996$
Hence, the answer is 996 .