Modulus of Complex Number - Properties, Formula, Graph and Examples

Modulus of complex number means the distance of the complex number from the origin of the argand plane. It also helps in finding the distance between two points of complex numbers. The modulus of a complex number is also called the absolute value of the complex number.

In this article, we will cover the concept of the modulus of a complex number. This concept falls under the broader category of complex numbers. It is essential not only for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), as well as other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of seventeen questions have been asked on this concept, including two in 2013, two in 2014, one in 2015, one in 2019, three in 2020, three in 2021, three in 2022, and two in 2023.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What is Modulus of Complex Number?
2. Modulus of Complex Number Formula
3. Modulus of a complex number using graph
4. Summary
5. Solved Examples Based on Modulus of Complex Number

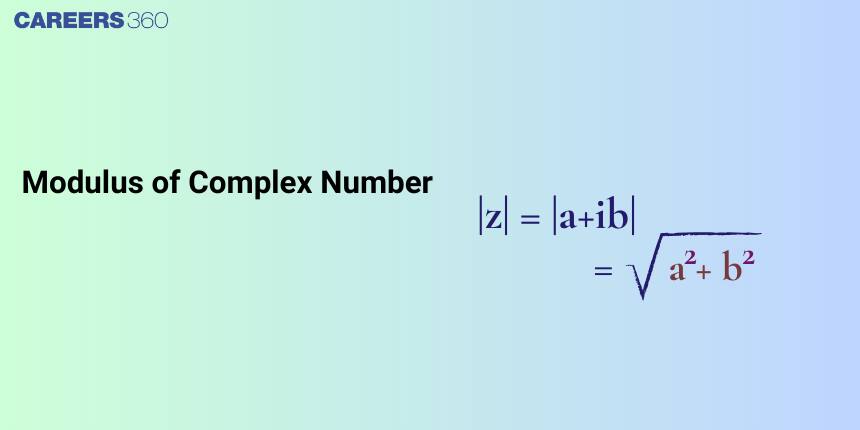
What is Modulus of Complex Number?

If z = x + iy is a complex number. Then, the modulus of z, denoted by | z |, is the distance of z from the origin in the Argand plane, and it is a non-negative real number equal to $\sqrt{x^2+y^2}$.

i.e. |z| =$\sqrt{\mathrm{x}^2+\mathrm{y}^2}$.

Every complex number can be represented as a point in the argand plane with the x-axis as the real axis and the y-axis as the imaginary axis.

$|z|=\sqrt{x^2+y^2}=r$ (length r from origin to point (x,y))

Modulus of Complex Number Formula

The modulus of a complex number $z=x+i y$, denoted by |z|, is given by the formula $|z|=\sqrt{ }\left(x^2+y^2\right)$ where x is the real part and y is the imaginary part of the complex number z. The modulus of the complex number z can also be calculated using the conjugate of z. Since $z . \bar{z}=(x+i y)(x-i y)=x^2+y^2 \space{\text {we have }} z \cdot \bar{z}=|z|^2 \Rightarrow \sqrt{z \cdot \bar{z}}$

Modulus of a complex number using graph

The distance between the complex number's coordinates and the origin on a complex plane, as shown in a graph of a complex number $\mathbf{z}$, is known as the complex number's modulus. The modulus of a complex number is the distance of the number expressed as a point on the argand plane (x, y). This distance, expressed as $r=\sqrt{(x^2+y^2) }$, is a linear distance between the origin $(0,0)$ and the point $(x, y)$.

Moreover, this can be interpreted in terms of the Pythagorean theorem, which states that the hypotenuse, base, and height of a right-angled triangle reflect the modulus, real portion, and imaginary part, respectively, of a complex number. The magnitude (or length) of the vector that represents $x + yi$ is equal to the modulus of a complex number, $\mathrm{x}+\mathrm{yi}$.

Properties of Modulus

i) $|z| \geq 0$

ii)$|z|=0$, iff $z=0$ and $|z|>0$, iff $z \neq 0$

iii)$-|z| \leq \operatorname{Re}(z) \leq|z|$ and $-|z| \leq \operatorname{Im}(z) \leq|z|$

iv) $z|=| \bar{z}|=|-z|=|-\bar{z} \mid$

v) $z \bar{z}=|z|^2$

vi) $z_1 z_2|=| z_1|| z_2 \mid$. Thus,$\left|z^n\right|=|z|^n$

vii) $\left|\frac{z_1}{z_2}\right|=\frac{\left|z_1\right|}{\left|z_2\right|}$

viii) $\left|z_1 \pm z_2\right| \leq\left|z_1\right|+\left|z_2\right|$ (Triangle inequality) This can be generalized for n complex numbers.

iх) $\left|z_1 \pm z_2\right| \geq|| z_1|-| z_2||$

Summary

We concluded that the modulus is an important term in complex numbers that are used to find the distance from the origin. Like the distance formula in coordinate geometry, it seems to be similar to this for calculating distance. It is also applied in real-life scenarios to find the distance between two points in a complex plane or argand plane.

Recommended Video :

Solved Examples Based on Modulus of Complex Number

Example 1: The complex number satisfying $|z|=2$ will be:

1) $z=1+i$

2) $z=\sqrt{3}-i$

3) $\sqrt{2}+i$

4) $z=1-i$

Solution:

As we learned in

Definition of Modulus of z(Complex Number) -

$|z|=\sqrt{a^2+b^2}$ is the distance of z from the origin in the Argand plane

- wherein

Real part of $z=\operatorname{Re}(z)=$ a \& Imaginary part of $z=\operatorname{Im}(z)=b$

Now,

if $z=1+i$, then $|z|=\sqrt{1^2+1^2}=\sqrt{2}$

if $z=\sqrt{3}-i$, then $|z|=\sqrt{(\sqrt{3})^2+(-1)^2}=\sqrt{3+1}=2$

if $z=\sqrt{2}+i$, then $|z|=\sqrt{(\sqrt{2})^2+1^2}=\sqrt{2+1}=\sqrt{3}$

if $z=1+i$ then $|z|=\sqrt{1^2+(-1)^2}=\sqrt{1+1}=\sqrt{2}$

Hence, the answer is the option (2).

Example 2: Let $z=-12-5 i$ and $w=2 \sqrt{11}+i y$ such that z and w both are equidistant from origin then y equals Where $y \in R$

1) $2 \sqrt{5}$
2) $3 \sqrt{5}$
3) $4 \sqrt{5}$
4) $5 \sqrt{5}$

Solution

As we learned in

Definition of Modulus of z(Complex Number) -

$|z|=\sqrt{a^2+b^2}$ is the distance of z from the origin in the Argand plane

- wherein

Real part of $z=\operatorname{Re}(z)=a$ \& Imaginary part of $z=\operatorname{Im}(z)=b$

z & w are equidistant from origin so $|z|=|w|$

$\begin{aligned} & \Rightarrow \sqrt{144+25}=\sqrt{44+y^2} \\ & \Rightarrow \sqrt{169}=\sqrt{44+y^2} \\ & \Rightarrow 169=44+y^2 \\ & \Rightarrow y^2=125 \\ & \Rightarrow y= \pm 5 \sqrt{5}\end{aligned}$

Hence, the answer is $5 \sqrt{5}$

Example 3: Let $w(\operatorname{Im} w \neq 0)$ be a complex number. Then the set of all complex numbers z satisfying the equation $w-\bar{w} z=k(1-z)$ for some real number k is :

1) $\{z:|z|=1\}$

2) $\{z: z=\bar{z}\}$

3) $\{z: z \neq 1\}$

4) $\{z:|z|=1, z \neq 1\}$

Solution

As we have learned

Property of Modulus of z(Complex Number) -

$\frac{z_1}{z_2} \left\lvert\,=\frac{\left|z_1\right|}{\left|z_2\right|}\right.$

- where |.| denotes the modulus of a complex number

Now,

$\omega-\bar{\omega} z=k(1-z)$

$\Rightarrow \omega-k=\bar{\omega} z-k z$

$\Rightarrow z=\frac{\omega-k}{\bar{\omega}-k} \neq$

And

$\Rightarrow|z|=\frac{|\omega-k|}{|\bar{\omega}-k|}$

$=\frac{|x+i y-k|}{|x-i y-k|}$

$=\frac{\sqrt{(x-k)^2+y^2}}{\sqrt{(x-k)^2+y^2}}=1$

Hence, the answer is the option 4.

Example 4: If a>0 and $z=\frac{(1+i)^2}{a-i}$ , has magnitude $\sqrt{\frac{2}{5}}$ , then $[\bar{z} \mathrm{i}$ is equal to :

Solution:

Multiplication of Complex Numbers -

(a+ib)(c+id)=(ac-bd)+i(bc+ad)

Definition of Modulus of z(Complex Number) -

$|z|=\sqrt{a^2+b^2}$ is the distance of z from the origin in the Argand plane

- wherein

Real part of z = Re (z) = a & Imaginary part of z = Im (z) = b

$z=\frac{(1+i)^2}{a-i}$

$=\frac{1+2 i-1}{a-i}=\frac{2 i}{a-i}$

$z=\frac{2 i}{a-i} \times \frac{a+i}{a+i}=\frac{2 i(a+i)}{a^2+1}$

given that

$|z|=\sqrt{\frac{2}{5}}$

$\left|\frac{2 i(a+i)}{a^2+1}\right|=\sqrt{\frac{2}{5}}$

$\frac{2}{\sqrt{a^2+1}}=\sqrt{\frac{2}{5}}$

$a=3$

$z=-\frac{1}{5}-\frac{3 i}{5}$

Hence, the answer is $-\frac{1}{5}-\frac{3}{5} i$

Example 5:The equation $|z-i|=|z-1|, i=\sqrt{-1}$ represents:

1) a circle of radius $\frac{1}{2}$.

2) a circle of radius

3) the line through the origin with slope

4) the line through the origin with slope

Solution:

Definition of Complex Number -

$z=x+i y, x, y \in R \& i^2=-1$

- wherein

Real part of $z=\operatorname{Re}(z)=x \&$ Imaginary part of $z=\operatorname{Im}(z)=y$

Definition of Modulus of z(Complex Number) -

$|z|=\sqrt{a^2+b^2}$ is the distance of z from the origin in the Argand plane

- wherein

Real part of $z=\operatorname{Re}(z)=a$ \& Imaginary part of $z=\operatorname{Im}(z)=b$

$\begin{aligned} & |z-i|=\mid z-1 \\ & |x+i y-i|=|x+i y-1| \\ & |x+i(y-1)|=|(x-1)+i y| \\ & \sqrt{x^2+(y-1)^2}=\sqrt{(x-1)^2+y^2} \\ & x^2+(y-1)^2=(x-1)^2+y^2 \\ & x^2+y^2+1-2 y=x^2+1-2 x+y^2 \\ & -2 y=-2 a\end{aligned}$

$y=x$

The line through the origin with slope 1