Nature of Roots of Quadratic Equations: Formulas and Examples
Roots are the solutions to various types of equations. In mathematics, the nature of roots refers to the characteristics and properties of these solutions. Roots are the values that satisfy the equation, making it true. Understanding the nature of roots is crucial for solving equations in fields like science, engineering, and statistics. Depending on the equation, roots can be real or imaginary, and their behavior can offer valuable insights into mathematical relationships.
JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days
JEE Main 2025: Maths Formulas | Study Materials
JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics
- What are the Roots of Quadratic Equation?
- Types of roots
- How to Find the Nature of Roots?
- Nature of Roots Graph
- Nature of Roots depending upon Coefficient
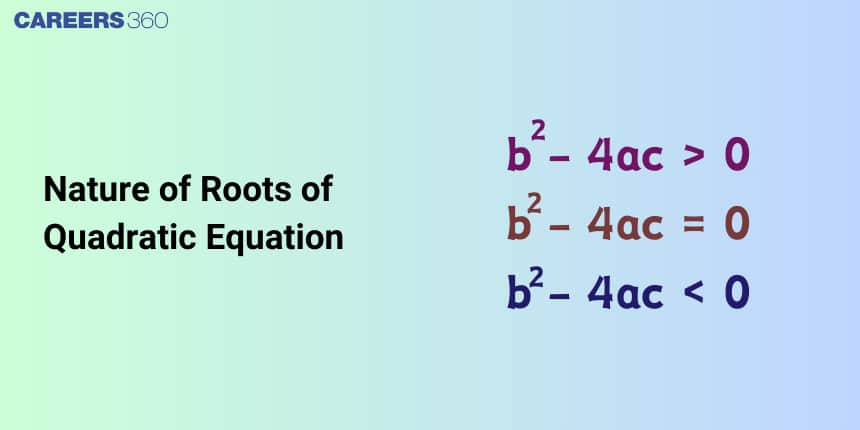
In this article, we will cover the concept of the nature of roots depending upon coefficients and discriminants. This concept falls under the broader category of complex numbers and quadratic equations, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more.
What are the Roots of Quadratic Equation?
In this context, the term “roots” refers to the values of the variable (usually denoted as “x”) that satisfy the equation, making it true. We know that the standard representation of a Quadratic Equation is given as ax2 + bx + c = 0. The roots of a quadratic equation are the values of “x” that, when substituted into the equation, make the equation true (i.e., equal to zero). There can be zero, one, or two real roots (values of “x”) depending on the discriminant (the value inside the square root) of the equation.
Let the quadratic equation is $a x^2+b x+c=0,(a, b, c \in R)$
$D$ (called the discriminant of the equation) $=b^2-4 a c$
The roots of this equation are given by
$
\mathrm{x}_1=\frac{-b+\sqrt{D}}{2 a} \text { and } x_2=\frac{-b-\sqrt{D}}{2 a}
$
Types of roots
Real and Distinct Roots
- The discriminant is positive, that is, $b^2−4ac>0$.
- The curve intersect the x-axis at two distinct points.
Real and Equal Roots
- The discriminant is equal to zero, that is, $b^2−4ac=0$.
- The curve intersects the x-axis at only one point.
Complex Roots
- The discriminant is negative, that is, $b^2−4ac<0$.
- The curve does not intersect the $x-$axis.
What is the Nature of Roots in Quadratic Equation?
Quadratic equations are polynomial equations of degree two that can have a maximum of two roots or solutions. The nature of roots provides us with these roots or solutions. In the phrase "nature of roots," "nature" refers to the kind of number—real, complex, rational, irrational, equal, or unequal—that the equation's root is. Without explicitly factorizing or solving the quadratic equation, we can rapidly determine if it has one real root, two real roots, or two complex roots by using the method of determining the type of roots.
The nature of the roots formula for the quadratic equation $a x^2+b x+c=0$ is $b^2-
4 ac$ . It is called the discriminant of the quadratic equation and is used to discriminate and draw conclusions about the roots of the quadratic equation.
We have 3 different types of roots depending on their nature. We use $b^2$ - $4 a c$ i.e, the discriminant to obtain the nature of roots.
i) if $D<0$, then both roots are non-real (imaginary numbers), and the roots will be conjugate of each other, which means if $p+i q$ is one of the roots then the other root will be p - iq
ii) If $D>0$, then roots will be real and distinct
iii) if roots $D=0$, then roots will be real and equal, and they equal
$
\mathrm{x}_1=\mathrm{x}_2=\frac{-\mathrm{b}}{2 \mathrm{a}}
$
Special cases of case $(D>0)$
i) if a,b,c are rational numbers $(Q)$ and
If $D$ is a perfect square, then roots are rational
If $D$ is not a perfect square then roots are irrational (in this case if $p+\sqrt{q}$ is one root of the quadratic equation then other roots will be $p-\sqrt{q}$ )
ii) If $a=1$ and b and c are integers and
If $D$ is a perfect square, then roots are integers
If $D$ is not a perfect square then roots are non-integer values
How to Find the Nature of Roots?
Let’s see the steps on how we can find the nature of roots with an example.
Step 1: Compare the given quadratic equation with the standard form of quadratic equations $a x^2+b x+c=0$ and find the values for the coefficients $a, b$, and $c$.
Step 2: Substitute the value of the coefficients in the discriminant equation $b^2-4 a c$ and solve it
Step 3: Observe the value you get for the discriminant. If it is less than zero you have complex roots. If it is equal to zero you have real and equal roots. If it is greater than zero you have real and distinct roots.
| $b^2-4 a c>0$ | Real and unequal |
| $b^2-4 a c = 0$ | Real and equal |
| b2 – 4ac < 0 | Unequal and Imaginary |
| $b^2-4 a c>0$ (is a perfect square) | Real, rational and unequal |
| $b^2-4 a c>0$ (is not a perfect square) | Real, irrational and unequal |
| $b^2-4 a c>0$ (is a perfect square and a or b is irrational) | Irrational |
Nature of Roots Graph
The roots of an equation are the solutions of the equation. Thus, at the roots of an equation, the graph of the equation will intersect the $x$-axis. Depending on the nature of the roots we have the following graphs:
- For $D>0$, we have real and distinct roots and the graph of the quadratic equation in variable $x$ will coincide with the $x$ -axis at two distinct points.
- For $\mathrm{D}=0$, we have only one real root and the graph of the quadratic equation touches the $x$-axis at a single point.
- For $D<0$, we have no real root and thus the graph of the quadratic equation does not touch the $x$-axis.
Nature of Roots depending upon Coefficient
Depending upon the values of the coefficients; $a, b$, and $c$ of the quadratic equation $\mathrm{ax}^2+\mathrm{bx}+\mathrm{c}=0$ we can conclude the following about the nature of its roots:
- If $c=0$, one of the roots of the quadratic equation is zero and the other is $-\mathrm{b} / \mathrm{a}$.
This can be shown by substituting $\mathrm{c}=0$ in the formula for the roots;
$x= \frac{-b \pm \sqrt{b^2-4 a c}}{2 a}$
$ x=\frac{-b \pm b}{2 a} \quad \text { Thus, } \mathrm{x}=0 \text { or } \mathrm{x}=-\mathrm{b} / \mathrm{a} .$
- If $b=c=0$, then both the roots are zero. To show this substitute $b=c=0$ in
$x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}$
Let $\alpha$ and $\beta$ be two roots of a quadratic equation. So, we have
$\alpha=\frac{-b-\sqrt{D}}{2 \mathrm{a}} $
$ \beta=\frac{-\mathrm{b}+\sqrt{\mathrm{D}}}{2 \mathrm{a}}$
Let $\alpha$ and $\beta$ be two roots of a quadratic equation. So, we have
$
\begin{aligned}
& \alpha=\frac{-b-\sqrt{D}}{2 \mathrm{a}} \\
& \beta=\frac{-\mathrm{b}+\sqrt{\mathrm{D}}}{2 \mathrm{a}}
\end{aligned}
$
Sum of roots
$
\alpha+\beta=\frac{-\mathrm{b}-\sqrt{\mathrm{D}}}{2 \mathrm{a}}+\frac{-\mathrm{b}+\sqrt{\mathrm{D}}}{2 \mathrm{a}}=\frac{-\mathrm{b}}{\mathrm{a}}
$
Product of roots
$
\begin{aligned}
& \alpha \cdot \beta=\left(\frac{-\mathrm{b}-\sqrt{\mathrm{D}}}{2 \mathrm{a}}\right) \cdot\left(\frac{-\mathrm{b}+\sqrt{\mathrm{D}}}{2 \mathrm{a}}\right) \\
& =\frac{\mathrm{b}^2-\mathrm{D}}{4 \mathrm{a}^2}=\frac{\mathrm{b}^2-\mathrm{b}^2+4 \mathrm{ac}}{4 \mathrm{a}^2}=\frac{4 \mathrm{ac}}{4 \mathrm{a}^2}=\frac{\mathrm{c}}{\mathrm{a}}
\end{aligned}
$
The difference of root can also be found in the same way by manipulating the terms
$
\alpha-\beta=\left|\frac{\sqrt{D}}{a}\right|
$
Important Results
(i) $\alpha^2+\beta^2=(\alpha+\beta)^2-2 \alpha \beta$
(ii) $\alpha^2-\beta^2=(\alpha+\beta)(\alpha-\beta)$
(iii) $\alpha^3+\beta^3=(\alpha+\beta)^3-3 \alpha \beta(\alpha+\beta)$
(iv) $\alpha^3-\beta^3=(\alpha-\beta)^3+3 \alpha \beta(\alpha-\beta)$
Recommended Video Based on the Nature of Roots
Solved Examples Based on the Nature of Roots
Example 1: If $\alpha$ and $\beta$ are roots of the equation, $x^2-4 \sqrt{2} k x+2 e^{4 \ln k}-1=0$ for some $k$ and $\alpha^2+\beta^2=66$ then $\alpha^3+\beta^3$ is equal to:
Solution:
As we have learned
The sum of Roots in Quadratic Equation -
$
\alpha+\beta=\frac{-b}{a}
$
- wherein
$\alpha$ and $\beta$ are the root of quadratic equation
$
\begin{aligned}
& a x^2+b x+c=0 \\
& a, b, c \in C
\end{aligned}
$
Product of Roots in Quadratic Equation -
$
\alpha \beta=\frac{c}{a}
$
- wherein
$\alpha$ and $\beta$ are roots of a quadratic equation:
$
\begin{aligned}
& a x^2+b x+c=0 \\
& a, b, c \in C
\end{aligned}
$
$
\alpha \beta=\frac{c}{a}
$
- wherein
$\alpha$ and $\beta$ are roots of a quadratic equation:
$
\begin{aligned}
& a x^2+b x+c=0 \\
& a, b, c \in C \\
& x^2-4 \sqrt{2} k x+2 e^{\ln k^4}-1=0 \\
& \Rightarrow x^2-4 \sqrt{2} k x+2 k^4-1=0 \\
& \alpha+\beta=4 \sqrt{2} k \text { and } \\
& \alpha \beta=2 k^4-1
\end{aligned}
$
Now, $\alpha^2+\beta^2=(\alpha+\beta)^2-2 \alpha \beta$
$
\begin{aligned}
& \Rightarrow 66=32 k^2-4 k^4+2 \\
& \Rightarrow 4 k^4-32 k^2+64=0 \\
& \Rightarrow k^4-8 k^2+16=0 \\
& \Rightarrow\left(k^2-4\right)=0 \\
& \Rightarrow k= \pm 2
\end{aligned}
$
$k= 2$ acceptable for ln $k$ to be definite
$
\begin{aligned}
& \therefore \alpha^3+\beta^3=(\alpha+\beta)^3-3 \alpha \beta(\alpha+\beta)=(4 \sqrt{2} \times 2)^3-3(32-1)(4 \sqrt{2} \times 2) \\
& =1024 \sqrt{2}-744 \sqrt{2}=280 \sqrt{2}
\end{aligned}
$
Hence, the answer is $280 \sqrt{2}$.
Example 2: if $\frac{1}{\sqrt{\alpha}}$ and $\frac{1}{\sqrt{\beta}}$ are the root of the equation $a x^2+b x+1=0$ $(a \neq 0, a, b, \epsilon R)$, then the equation $x\left(x+b^3\right)+\left(a^3-3 a b x\right)=0$ has root
1) $\alpha^{\frac{3}{2}}$ and $\beta^{\frac{3}{2}}$
2) $\alpha \beta^{\frac{1}{2}}$ and $\alpha^{\frac{1}{2}} \beta$
3) $\sqrt{\alpha \beta}$ and $\alpha \beta$
4) $\alpha^{-\frac{3}{2}}$ and $\beta^{-\frac{3}{2}}$
Solution:
We have,
$
\begin{aligned}
& \frac{1}{\sqrt{\alpha}}+\frac{1}{\sqrt{\beta}}=\frac{-b}{a} \\
& \frac{1}{\sqrt{\alpha \beta}}=1 / a
\end{aligned}
$
Now, $x^2-3 a b x+b^3 x+a^3=0$
$\Rightarrow x^2+\left(b^3-3 a b\right) x+a^3=0$
$\left(\right.$ since $\alpha \beta=a^2$ and $\left.\frac{\sqrt{\alpha}+\sqrt{\beta}}{a}=-b / a \Rightarrow \sqrt{\alpha}+\sqrt{\beta}=-b\right)$
$
\begin{aligned}
& \Rightarrow x^2+(-(\sqrt{\alpha}+\sqrt{\beta}))\left((\sqrt{\alpha}+\sqrt{\beta})^2-3 \sqrt{\alpha \beta}\right) x+(\alpha \beta)^{3 / 2}=0 \\
& \Rightarrow x^2-\left((\sqrt{\alpha}+\sqrt{\beta})^3-3 \alpha \sqrt{\beta}-3 \sqrt{\alpha} \beta\right) x+(\alpha \beta)^{3 / 2}=0 \\
& \Rightarrow x^2-\left(\left(\sqrt{\alpha}^{\frac{3}{2}}+\sqrt{\beta^{\frac{3}{2}}}\right) x+(\alpha \beta)^{3 / 2}=0\right.
\end{aligned}
$
The roots are $\alpha^{\frac{3}{2}}$ and $\beta^{\frac{3}{2}}$
Hence, the answer is the option 1.
Example 3: If, for a positive integer n , the quadratic equation,
$
\begin{aligned}
& x(x+1)+(x+1)(x+2)+\ldots \\
& +(x+\overline{n-1})(x+n)=10 n
\end{aligned}
$
has two consecutive integral solutions, then $\boldsymbol{n}$ is equal to :
Solution:
As we learned in
Condition for Real and Distinct Roots of Quadratic Equation -
$
D=b^2-4 a c>0
$
wherein
$
a x^2+b x+c=0
$
is the quadratic equation
$
x(x+1)+(x+1)(x+2)+\ldots \ldots \ldots(x+(\overline{n-1}))(x+n)=10 n
$
$
\begin{aligned}
& \left(x^2+x\right)+\left(x^2+3 x+2\right)+\left(x^2+5 x+6\right)+\ldots \ldots \ldots\left[x^2+(n-1+n) x+n(n-1)\right]=10 n \\
& \Rightarrow \quad \sum x^2+\sum(n+n-1) x+\sum n(n-1)=10 n \\
& \Rightarrow n x^2+\sum(2 n-1) x+\sum\left(n^2-n\right)=10 n \\
& \Rightarrow n x^2+[n(n+1)-n] x+\left[\frac{n(2 n+1)(n+1)}{6}-\frac{n(n+1)}{2}\right]=10 n \\
& \Rightarrow n x^2+n^2 x+\left[\frac{n(n+1)(2 n+1-3)}{6}\right]=10 n \\
& \Rightarrow n x^2+n^2 x+\left[\frac{n(n+1)(n-1)}{3}\right]=10 n \\
& \Rightarrow x^2+n x+\frac{n^2-1}{3}=10 \\
& \Rightarrow x^2+n x+\frac{n^2-31}{3}=0 \\
& B^2-4 A C \geq 0 \\
& \therefore n^2-\frac{4}{3}\left(n^2-31\right) \geq 0 \\
& \therefore n^2 \leq 124
\end{aligned}
$
So maximum value $n$ is 11 .
Hence, the answer is 11 .
Example 4: If the two roots of the equation,
$
(a-1)\left(x^4+x^2+1\right)+(a+1)\left(x^2+x+1\right)^2=0
$
are real and distinct, then the set of all values of ' $a$ ' is :
1) $\left(-\frac{1}{2}, 0\right)$
2) $(-\infty,-2) \cup(2, \infty)$
3) $\left(-\frac{1}{2}, 0\right) \cup\left(0, \frac{1}{2}\right)$
4) $\left(0, \frac{1}{2}\right)$
Solution:
As we learned in
Condition for Real and Distinct Roots of Quadratic Equation -
$
D=b^2-4 a c>0
$
- wherein
$
a x^2+b x+c=0
$
is the quadratic equation
$
\begin{aligned}
& (a-1)\left(x^4+x^2+1\right)+(a+1)\left(x^2+x+1\right)^2=0 \\
& \Rightarrow \quad(a-1)\left(x^2+2 x^2+1-x^2\right)+(a+1)\left(x^2+x+1\right)^2=0 \\
& \Rightarrow \quad(a-1)\left(\left(x^2+1\right)^2-x^2\right)+(a+1)\left(x^2+x+1\right)^2=0
\end{aligned}
$
$
\begin{aligned}
& \Rightarrow \quad(a-1)\left(x^2+1+x\right)\left(x^2+1-x\right)+(a+1)\left(x^2+x+1\right)^2=0 \\
& \Rightarrow \quad\left(x^2+x+1\right)\left((a-1)\left(x^2-x+1\right)\right)+(a+1)\left(x^2+x+1\right)=0 \\
& \Rightarrow \quad x^2+x+1 \neq 0 \\
& \text { So }(a-1)\left(x^2-x+1\right)+(a+1)\left(x^2+x+1\right)=0 \\
& \Rightarrow \quad 2 a x^2+2 x+2 a=0 \\
& \Rightarrow \quad a x^2+x+a=0
\end{aligned}
$
So for real value of $\mathrm{x} \geq 0$
$
\begin{aligned}
\therefore \quad & 1-4 . a \cdot a \geq 0 \\
& 1 \geq 4 a^2 \Rightarrow 4 a^2 \leq 1 \\
& \therefore \quad \frac{-1}{2} \leq a \leq \frac{1}{2}
\end{aligned}
$
But $a \neq 0$
So
$
a \epsilon\left(\frac{-1}{2}, 0\right) \bigcup\left(0, \frac{1}{2}\right)
$
Hence, the answer is the option 3.
Example 5: Equation $3 x^2+6 x+2=0$ will have
1) Real & Equal roots
2) Real & Distinct roots
3) Imaginary roots
4) Can't be determined
Solution:
As we learned in
Condition for Real and Distinct Roots of Quadratic Equation -
$
\begin{aligned}
& D=b^2-4 a c>0 \\
& \text { - wherein } \\
& a x^2+b x+c=0
\end{aligned}
$
is the quadratic equation
$
D=(6)^2-4(3)(2)=36-24=12>0
$
Hence, the answer is the option 2
Frequently Asked Questions (FAQs)
A polynomial that has degree two is called a quadratic equation.
The discriminant of the quadratic equation is given by $D = b^2-4ac.$
If discriminant, $D = 0$, then the roots are real and equal.
If discriminant, $D>0$, then the roots are real and unequal.
If discriminant, $D<0$, then the roots are imaginary and unequal.
Also Read
10 Feb'25 11:53 PM
10 Feb'25 11:50 PM
10 Feb'25 11:30 PM
10 Feb'25 09:26 PM
10 Feb'25 09:23 PM
10 Feb'25 09:16 PM
10 Feb'25 08:47 PM
10 Feb'25 08:39 PM
10 Feb'25 08:31 PM
10 Feb'25 08:26 PM