Normal at t1 meets the parabola again at t2

In the study of parabolas, understanding the behaviour of normals is essential for various applications in mathematics and physics. A normal to a parabola at a given point is a line that is perpendicular to the tangent at that point. An interesting property of the normal is that it intersects the parabola at another point. This property is particularly intriguing in the context of parametric equations where points on the parabola are described by parameters.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What is Parabola?
2. Normal at t1 meets the parabola again at t2
3. Solved Questions Based on Normal at t1 Meets the Parabola Again at t2

What is Parabola?

A parabola is the locus of a point moving in a plane such that its distance from a fixed point (focus) is equal to its distance from a fixed line (directrix).

$\begin{equation}
\text { Hence it is a conic section with eccentricity e }=1 \text {. }
\end{equation}$

$\begin{aligned} & \frac{P S}{P M}=e=1 \\ & \Rightarrow P S=P M\end{aligned}$

Standard equation of a parabola

If the directrix is parallel to the y-axis in the standard equation of a parabola is given as
$
y^2=4 a x
$
If the directrix is parallel to the $x$-axis, the standard equation of a parabola is given as

$
x^2=4 a y
$

Normal at t₁ meets the parabola again at t₂

A Parabola is a U- shaped plane curve where any point is at an equal distance from a fixed point and from a fixed straight line. The line perpendicular to the tangent to the curve at the point of contact is normal to the parabola. In real life, we use a parabolic antenna or parabolic microphone.

Equation of Normal at $P \equiv\left(a t_1^2, 2 a t_1\right)$ to the parabola $y^2=4 a x$ is

$
y=-t_{1 x}+2 a t_1+a t_1^3
$
It meets the parabola again at $\mathrm{Q} \equiv\left(\mathrm{at}_2^2, 2 \mathrm{at}_2\right)$

$
\begin{aligned}
& \therefore 2 \mathrm{at}_2=-\mathrm{at}_1 \mathrm{t}_2^2+2 \mathrm{at}_1+\mathrm{at}_1^3 \\
& \Rightarrow 2 a\left(t_2-t_1\right)+a t_1\left(t_2^2-t_1^2\right)=0 \\
& \Rightarrow \mathrm{a}\left(\mathrm{t}_2-\mathrm{t}_1\right)\left[2+\mathrm{t}_1\left(\mathrm{t}_2+\mathrm{t}_1\right)\right]=0 \\
& \therefore 2+\mathrm{t}_1\left(\mathrm{t}_1+\mathrm{t}_2\right)=0
\end{aligned}
$
$
t_2=-t_1-\frac{2}{t_1}
$

Recommended Video Based on Normal at t₁ Meets the Parabola Again at t₂

Solved Questions Based on Normal at t₁ Meets the Parabola Again at t₂

Example 1: Two normals at t₁ and t₂ meet again the parabola y² = 4ax then the relation between t₁ and t₂ is

$\begin{aligned} & \text { 1) } t_1 t_2=1 \\ & \text { 2) } t_1-t_2=2 \\ & \text { 3) } t_1 t_2=2 \\ & \text { 4) } t_1+t_2=2\end{aligned}$

Solution

Normal at t1 meets the parabola again at t2 -

Equation of Normal at $\mathrm{P} \equiv\left(\mathrm{at}_1^2, 2 a t_1\right)$ to the parabola $\mathrm{y}^2=4 \mathrm{ax}$ is

$
=-\mathrm{t}_{1 \mathrm{X}}+2 \mathrm{at}_1+\mathrm{at}_1^3
$
It meets the parabola again at $\mathrm{Q} \equiv\left(\mathrm{at}_2^2, 2 \mathrm{at} 2\right)$

$
\begin{aligned}
& 2 \mathrm{at}_2=-\mathrm{at}_1 \mathrm{t}_2^2+2 \mathrm{at}_1+\mathrm{at}_1^3 \\
& \Rightarrow 2 \mathrm{a}\left(\mathrm{t}_2-\mathrm{t}_1\right)\left[2+\mathrm{at}_1\left(\mathrm{t}_2^2-\mathrm{t}_1^2\right)=0\right. \\
& \Rightarrow \mathrm{a}\left(\mathrm{t}_2-\mathrm{t}_1\right)\left[2+\mathrm{t}_1\left(\mathrm{t}_2+\mathrm{t}_1\right)\right]=0 \\
& a\left(t_2-t_1\right)=0 \\
& 2+\mathrm{t}_1\left(\mathrm{t}_1+\mathrm{t}_2\right)=0 \\
& 2=-\mathrm{t}_1-\frac{2}{\mathrm{t}_1}
\end{aligned}
$

Since the normal at $t_1$ meets the parabola at $t$, so

$
t=-t_1-\frac{2}{t_1}
$
Similarly,
Thus, $-t_1-\frac{2}{t_1}=-t_2-\frac{2}{t_2}$

$
\begin{aligned}
& \Rightarrow \quad\left(t_1-t_2\right)=\left(\frac{2}{t_1}-\frac{2}{t_2}\right)^{t_2}=\frac{2\left(t_1-t_2\right)}{t_1 t_2} \\
& \Rightarrow \quad t_1 t_2=2
\end{aligned}
$

Example 2: Let the tangent to the parabola $\mathrm{S}: \mathrm{y}^2=2 \mathrm{x}$ at the point $\mathrm{P}(2,2)$ meet the x -axis at $Q$ and normal at it meet the parabola $S$ at the point $R$. Then the area (in sq. units) of the triangle $P Q R$ is equal to :
1) $\frac{25}{2}$
2) $\frac{35}{2}$
3) $\frac{15}{2}$
4)25

Solution

$
y^2=2 x \Rightarrow a=\frac{1}{2}
$
Equation of tangent at $P$ :

$
\begin{aligned}
& T=0 \\
& y y_1=2\left(\frac{x+x_1}{2}\right) \\
& 2 y=x+2
\end{aligned}
$
For point Q , put $y=0 \Rightarrow x=-2$

$
\therefore Q(-2,0)
$

Now point $R$
If P is $\left(\mathrm{at}^2, 2 \mathrm{at}\right)$, then point R will be

$
\begin{aligned}
& \quad\left(a\left(-t-\frac{2}{t}\right)^2, 2 a\left(-t-\frac{2}{t}\right)\right) \\
& P(2,2)=\left(a t^2, 2 a t\right) \\
& \Rightarrow \quad 2=2 a t \Rightarrow 2=2\left(\frac{1}{2}\right) t \Rightarrow t=2 \\
& \therefore \quad R=\left(\frac{1}{2}\left(-2-\frac{2}{2}\right)^2, 2\left(\frac{1}{2}\right)\left(-2-\frac{2}{2}\right)\right) \\
& \quad R\left(\frac{9}{2},-3\right) \\
& \quad \Delta P Q R=\left|\frac{1}{2}\right| \begin{array}{ccc}
2 & 2 & 1 \\
-2 & 0 & 1 \\
\frac{9}{2} & -3 & 1
\end{array}||=\frac{25}{2}
\end{aligned}
$

Hence, the correct answer is option (1).

Example 3: P and Q are two distinct points on the parabola, y² = 4x, with parameters t and t₁ respectively. If the normal at P passes through Q, then the minimum value of is:

1) 2

2) 4

3) 6

4) 8

Solution

Parametric coordinates of parabola -
$
\begin{aligned}
& x=a t^2 \\
& y=2 a t
\end{aligned}
$

- wherein

For the parabola.

$
y^2=4 a x
$
Parametric coordinates are $\left(a t^2, 2 a t\right)$ $t_1=-t-\frac{2}{t}($ Condition for normal chord $)$

$
t_{\text {so, }}^2=t^2+\frac{4}{t^2}+4
$
Using $A M>G M$

$
\frac{t^2+\frac{4}{t^2}}{2} \geq \sqrt{t^2 \cdot \frac{4}{t^2}}
$

Hence, the answer is the option (4)

Example 4: The normal at the point $\left(b t_1{ }^2, 2 b t_1\right)$ on a parabola meets the parabola again in the point $\left(b t_2{ }^2, 2 b t_2\right)$, then

$
\begin{aligned}
t_2 & =-t_1+\frac{2}{t_1} \\
t_2 & =t_1-\frac{2}{t_1} \\
t_2 & =t_1+\frac{2}{t_1} \\
t_2 & =-t_1-\frac{2}{t_1}
\end{aligned}
$

Solution
As we learnt in
Parametric coordinates of parabola -

$
\begin{aligned}
& x=a t^2 \\
& y=2 a t
\end{aligned}
$

- wherein

For the parabola.

$
y^2=4 a x
$

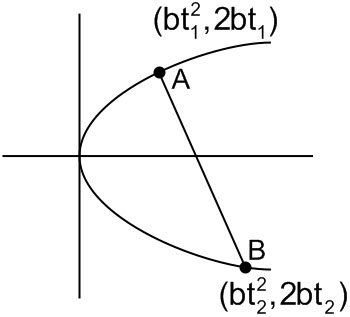
If $t_1$ and $t_2$ are the parameters

$
t_2=-t_1-\frac{2}{t_1}
$
Example 5: Circles are drawn taking any two focal chords of the parabola $y^2=4 a x$ as diameters. Then, the equation of a common chord is:
1) $a\left(t_3^2+t_4^2-t_1^2-t_2^2\right) x+a\left(t_3+t_4-t_1-t_2\right) y=0$
2) $a\left(t_3^2+t_4^2+t_1^2-t_2^2\right) x-2 a\left(t_3+t_4-t_1+t_2\right) y=0$
3) $a\left(t_3^2+t_4^2-t_1^2-t_2^2\right) x+2 a\left(t_3+t_4-t_1-t_2\right) y=0$
4) None of the above

Solution
Let $P Q$ and $R S$ be the two focal chords of the parabola and let $P, Q, R$, and $S$ be the points $t_1, t_2, t_3, t_4$ respectively, then $t_1 t_2=-1$ and $t_3 t_4=-1$. Clearly, a circle with PQ as the diameter is: $\square$

$
\begin{aligned}
\left(x-a t_1^2\right)\left(x-a t_2^2\right)+\left(y-2 a t_1\right)\left(y-2 a t_2\right) & =0 \\
\Rightarrow x^2+y^2-a\left(t_1^2+t_2^2\right) x-2 a\left(t_1+t_2\right) y-3 a^2 & =0
\end{aligned}
$
Circle with RS as the diameter is:

$
x^2+y^2-a\left(t_3^2+t_4^2\right) x-2 a\left(t_3+t_4\right) y-3 a^2=0
$

$\therefore$ Subtracting both the equations, we get the equation of the common chord as:

$
a\left(t_3^2+t_4^2-t_1^2-t_2^2\right) x+2 a\left(t_3+t_4-t_1-t_2\right) y=0
$
Hence, the answer is the option (3).

Summary

The normal at parabola intersects the parabola again showcasing an intriguing property of parabolas. By deriving the equations for the tangent and normal, and solving for their intersections, we gain valuable insights into the geometric and mathematical properties of parabolas. These concepts have practical applications in various fields, including physics, engineering, computer graphics, and optimization, highlighting their significance in both theoretical and applied mathematics.