Cartesian Product and Ordered Pairs

An ordered pair is a pair of elements with a specific order, usually written as (a,b). The order in which the elements are listed is crucial: (a,b)≠(b, a)unless a=b. In set theory, the cartesian product of two sets is the product of two non-empty sets in an ordered way. The Cartesian product comprises two words – Cartesian and product. The word Cartesian is named after the French mathematician and philosopher René Descartes (1596-1650).

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

In this article, we will cover the concept of the ordered pairs and cartesian products of two sets. This concept falls under the broader category of sets relation and function, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more.

Ordered pair

A pair of elements grouped together in a particular order is known as an ordered pair.
e.g. : $(a, b),(3,5),(-1,0) \ldots$

The ordered pairs (a, b) and (b, a) are different.
Two ordered pairs are equal, if and only if the corresponding first elements are equal and the second elements are also equal.
i.e. $(x, y)=(u, v)$ if and only if $x=u, y=v$.

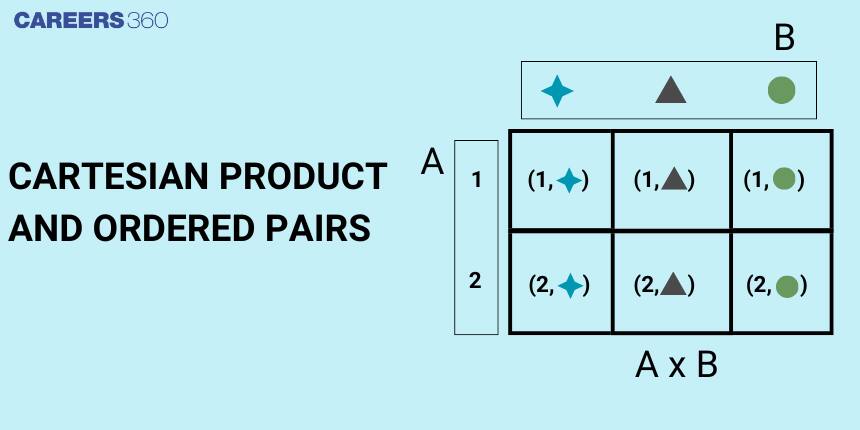
Cartesian product of sets

The cartesian product of two non-empty sets A and B is the set of all ordered pairs ( $x, y$ ), where $x \in A$ and $y \in B$.

Symbolically, we write it as $\mathrm{A} \times \mathrm{B}$ and it is read as ' A cross B '.

$$
A \times B=\{(a, b): a \in A, b \in B\}
$$
For example, If $A=\{1,2\}$ and $B=\{a, b\}$

Then $A \times B=\{(1, a),(1, b),(2, a),(2, b)\}$

Cartesian Product of Empty Set
As we know, an empty set does not have any elements. The cardinality of an empty set or the size is also zero. The cartesian product of a set, say A and the empty set $\phi$, is an empty set only.

$\mathrm{Ax}{ }^\phi=\phi$

Properties of Cartesian Product:
1. Non-commutative: The cartesian product of two sets is non-commutative because the order of elements is not the same.

$\begin{aligned}
& A \times B \neq B \times A \text { in general. For instance: } A \times B=\{(a, b) \mid a \in A \text { and } b \in B\} \\
& B \times A=\{(b, a) \mid b \in B \text { and } a \in A\}
\end{aligned}$

$A \times B$ and $B \times A$ contain different pairs unless $\mathrm{A}=\mathrm{B}$ and even then, the order of elements in the pairs is different.
2. Cardinality: If A has m elements and B has n elements, then $A \times B$ has $\mathrm{m} \times \mathrm{n}$ elements.

$|A \times B|=|A| \cdot|B|$

3. Associativity with Triples: For sets A, B, and C, the associative property is not applied due to unequal ordered.

$(A \times B) \times C \neq A \times(B \times C)$

However, both are sets of ordered pairs. Specifically:

$\begin{aligned}
& (A \times B) \times C=\{((a, b), c) \mid a \in A, b \in B, c \in C\} \\
& A \times(B \times C)=\{(a,(b, c)) \mid a \in A, b \in B, c \in C\}
\end{aligned}$

4. Distributive over Union: For sets A, B, and C, the distribution property of sets follow such rule-

$A \times(B \cup C)=(A \times B) \cup(A \times C)(A \cup B) \times C=(A \times C) \cup(B \times C)$

Number of elements in A x B

If there are $p$ elements in $A$ and $q$ elements in $B$, then there will be $p q$ elements in $A \times B$, i.e., if $n(A)=p$ and $n(B)=q$, then $n(A \times B)=p q$.

If $A, B, C$, and $D$ are any four sets, then
1. $A X(B \cup C)=(A \times B) \cup(A \times C)$
2. $A X(B \cap C)=(A X B) \cap(A X C)$
3. $A X(B-C)=(A X B)-(A X C)$
4. $(A \times B) \cap(C \times D)=(A \cap C) \times(B \times D)$
5. If $A \subseteq B$, then $(A X C) \subseteq(B \times C)$
6. If $A \subseteq B$, then $A \times A \subseteq(A X B) \cap(B \times A)$
7. If $A \subseteq B$ and $C \subseteq D$, then $A X C \subseteq B \times D$

Summary

We concluded that the understanding of ordered pairs and cartesian products is crucial in various areas of mathematics, computer science, and related fields. The concept of ordered pairs is fundamental in defining functions, where each input (from the domain) is paired with an output (from the codomain).

Recommended Video :

Solved Examples Based On the Ordered Pairs and Cartesian Product

Example 1: If a set has 20 elements. How many ordered pairs with distinct elements can be formed?

Solution:
As we learned
Let $A=\{1,2,3$ $20\}$

Let the ordered pair be $(a, b)$.
Selecting 2 elements from 20 elements is $\$\left\}^{\wedge}\{20\} \backslash\right.$ mathrm\{C\}_2\$
The number of ordered pairs $=\$\{ \}^{\wedge}\{20\}$ C_2=190\$
Hence, the answer is 190 .
Example 2: Given the set $A=\{1,2,3\}$. How many ordered pairs can be formed with both the elements belonging to set $A$ ?

Solution:
Ordered pairs can be $(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2)$ and $(3,3)$
So, a total of 9 such ordered pairs are possible.
Hence, the answer is 9 .
Example 3: What is the condition for $\mathrm{A} \times \mathrm{B}=\mathrm{B} \times \mathrm{A}$ being true?
1) Always true
2) Never true
3) When $A=B$
4) In most of the cases

If $A=B$, then
$A \times B=A \times A$ and
$B \times A=A \times A$
So, both are equal.
Hence, $A \times B=B \times A$ is true if both sets are identical.
Hence, the answer is the option 3.
Example 4: If the ordered pair $(x-3, y+2)$ is the same as $(5,9)$, then what are the values of $x$ and $y$ ?

Solution:

Equality of Ordered Pair

$\left(a_1, b_1\right)$ and $\left(a_2, b_2\right)$ are equal iff $a_1=a_2$ and $b_1=b_2$

So

x - 3 = 5 y = 7

x = 8

And

y + 2 = 9

Hence, the answer is x=8 and y=7.

Example 5: If $n(A)=5$ and $n(B)=7$ then $n(B \times A)$ equals
Solution:

$$
\begin{aligned}
n(B \times A) & =n(B) \times n(A) \\
& =7 \times 5=35
\end{aligned}
$$

Hence, the answer is 35 .

Frequently Asked Questions(FAQ)-

1. What is an ordered pair?

Ans: A pair of elements grouped together in a particular order is known as an ordered pair.

2. When will the two ordered pairs equal?

Ans: Two ordered pairs are equal, if and only if the corresponding first elements are equal and the second elements are also equal.

3. What is cartesian product?

Ans: The cartesian product of two non-empty sets $A$ and $B$ is the set of all ordered pairs ( $x, y$ ), where $\mathrm{x} \in \mathrm{A}$ and $\mathrm{y} \in \mathrm{B}$.
4. If $n(A x B)=40$ and $n(A)=4$, then find $n(B)$.

Ans: We know, that if $A$ and $B$ are finite sets, then $n(A \times B)=n(A) \cdot n(B)$
Here,
$40=\mathrm{n}(\mathrm{A}) \times \mathrm{n}(\mathrm{B})$
$\therefore n(B)=40 / 4=10$
5. If set $A=\{1,2,3\}$ and set $B=\{a, b\}$, then the Cartesian product $A x B$ is

Ans: As we learnedmim
The cartesian product is a set of ordered pairs of $(a, b)$ where $a \in A$ and $b \in B$.

$A=\{1,2,3\} \text { and } B=\{a, b\}$
Then, $A \times B=\{(1, a) ;(1, b) ;(2, a) ;(2, b) ;(3, a) ;(3, b)\}$