Permutations and Combinations in Mathematics focus on counting techniques used to arrange or select objects systematically. This chapter forms the basis of probability and is widely applied in problem-solving across school and competitive examinations.
Permutation and Combinations - Topics, Formula, Books, FAQs
Have you ever wondered how many different seating arrangements are possible in a classroom or how many teams can be formed from a group of players? Questions like these are answered using Permutations and Combinations, an important topic in mathematics that deals with counting. In Class 11 Mathematics, permutations refer to the different ways of arranging objects where order matters, while combinations deal with the selection of objects where order does not matter. For example, arranging books of different genres on a shelf involves permutations, whereas choosing a few books to read from the shelf is an example of combinations.
This Story also Contains
- Permutations and Combinations in Mathematics
- What are the Fundamental Principles of Counting?
- Relation between Permutation and Combination
- Difference between Permutation and Combination
- Permutations and Combinations in Mathematics: Solved Previous Year Questions
- Permutation and Combinations in Different Exams
- List of topics related to Permutations and Combinations according to JEE Mains/NCERT
- Best Books and Resources for Permutations and Combinations
- NCERT Resources for Permutations and Combinations
- NCERT Subjectwise Resources
- Practice Questions based on Permutations and Combinations
- Conclusion
Permutations and combinations have many real-life applications. They are used in probability, statistics, seating arrangements, team selection, password creation, and even in scheduling and planning. Because of their wide use, this chapter is frequently tested in school exams and competitive exams. In this article, you will learn permutations and combinations formulas, important concepts, shortcuts, and solved examples along with practice questions. These explanations will help you build strong conceptual clarity and master this topic efficiently for Class 11 exams and entrance examinations.
Permutations and Combinations in Mathematics
What is factorial?
A factorial is the product of all positive integers up to a given number.
It is denoted by $n!$.
$n!=n ×(n-1)×(n-2)×(n-3)×………×2 ×1$
It is calculated as follows.
$6! = 6 × 5 × 4 × 3 × 2 × 1 = 720$
Note that:
$1! = 1$
$0! = 1$
What is the meaning of $n!$?
$n!$ is read as “$n$ factorial”. It represents the products all positive integers from $1$ to $n$.
$n! = n × (n -1) × (n - 2) × (n - 3) × . . . . . . . × 1$
It is used in various mathematical and real-world contexts like:
-
Permutations and combinations
-
In calculations involving probability distributions.
-
Algebra and calculus
-
Computer science algorithms involving combinatorial logic.
What are the Fundamental Principles of Counting?
Fundamental Principle of Counting rules used to count the number of ways certain arrangements can occur.
It has two types.
-
Principle of Addition
-
Principle of Multiplication
JEE Main Highest Scoring Chapters & Topics
Focus on high-weightage topics with this eBook and prepare smarter. Gain accuracy, speed, and a better chance at scoring higher.
Download E-bookPrinciple of Addition(OR rule)
If work $W$ can be completed by doing task $A$ OR task$ B$, and $A$ can be done in $m$ ways and $B$ can be done in $n$ ways (and both cannot occur simultaneously: in this case, we call tasks $A$ and $B$ as mutually exclusive), hen work $W$ can be done in $(m+n)$ ways.
Principle of Multiplication(AND rule)
If a certain work $W$ can be completed by doing $2$ tasks, first doing task and then doing task $B$. A can be done in $m$ ways, and following that $B$ can be done in $n$ ways, then the number of ways of doing the work $W$ is $(m \times n)$ ways.
What is Permutation?
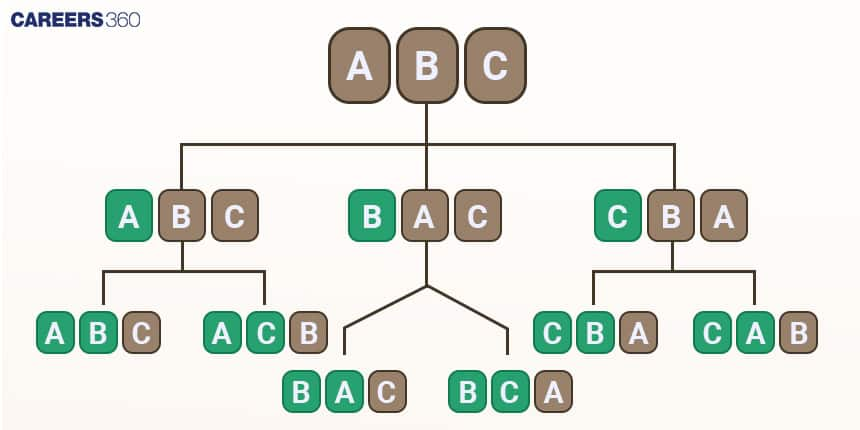
A permutation is an arrangement of all or part of a set of objects where order matters. Arranging $n$ objects in $r$ places means filling $r$ positions with $n$ distinct objects. For example, with letters $A, B, C$, the number of ways to arrange $2$ letters is $6$: $AB, AC, BA, BC, CA, CB$. Here, $n=3$ and $r=2$ show how permutations count ordered selections from $n$ objects taken $r$ at a time.
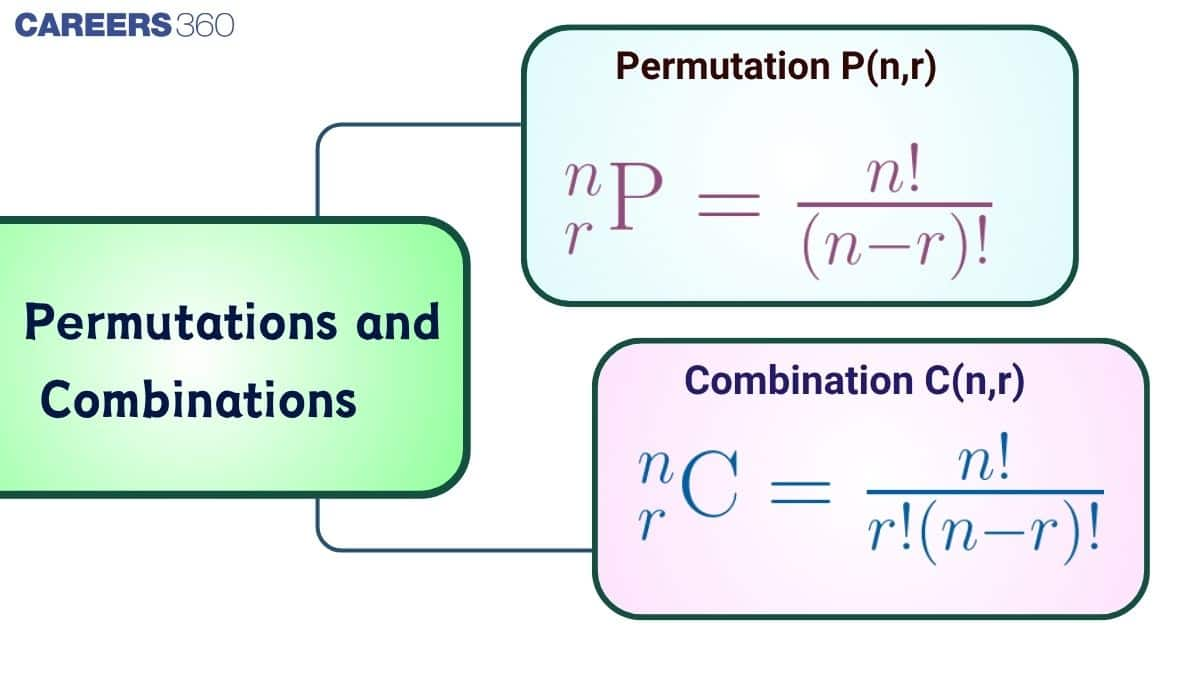
What is the formula for Permutation?
Arranging $n$ objects in $r$ places (Same as arranging $n$ objects taken $r$ at a time) is equivalent to filling $r$ places from $n$ things.
So the number of ways of arranging $n$ objects taken $r$ at a time $=n(n-1)$
$
\begin{aligned}
& (n-2) \ldots(n-r+1) \\
& \frac{n(n-1)(n-2) \ldots(n-r+1)(n-r)!}{(n-r)!}=\frac{n!}{(n-r)!}={ }^n P_r
\end{aligned}
$
Where $r \leq n$ and $r \in W$
So, the number of ways of arranging n different objects taken all at a time $=$ ${ }^n P_n=n!$
Types of Permutations
There are different types of permutations.
-
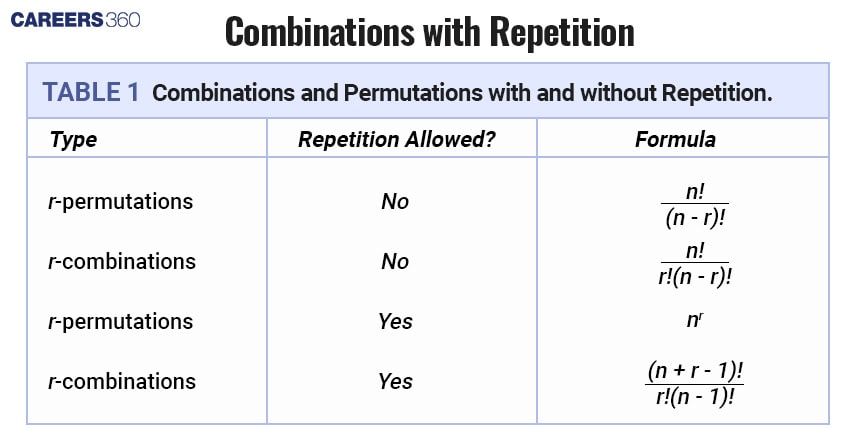
Permutation of $n$ different objects (when repetition is not allowed)
-
Repetition, where repetition is allowed
-
Permutation when the objects are not distinct (Permutation of multisets)
Permutation of $n$ different objects (when repetition is not allowed)
In this case, each object is used only once in the arrangement.
The formula to find the number of permutations of $n$ distinct objects is given by: $p(n) = n!$
Where $n!$ ($n$ factorial) is the product of all positive integers up to $n$
Permutation of $n$ different objects, where repetition is allowed
When repetition is allowed, each object can be used more than once in the arrangement. The formula to find the number of permutations when repetition is allowed is given by: $p(n,r) = nr$
Where $n$ is the total number of objects to choose from
And $r$ is the number of positions to be filled
Permutation when the objects are not distinct (Permutation of multisets)
When some objects are identical, the formula to find the number of distinct permutations is adjusted to account for the repetitions. The formula is given by:
$p(n: n_1, n_2, n_3,\ldots,......., n_k) = \frac{n!}{n_1! × n_2! × n_3! ×.........×n_k!}$
Where n is the number of total objects, $n_1, n_2, n_3,\ldots......., n_k$ are the frequencies of different objects.
What is Circular Permutation?
When n objects are to be arranged circularly, then the formula to find the number of distinct permutations is given by (n-1)!.
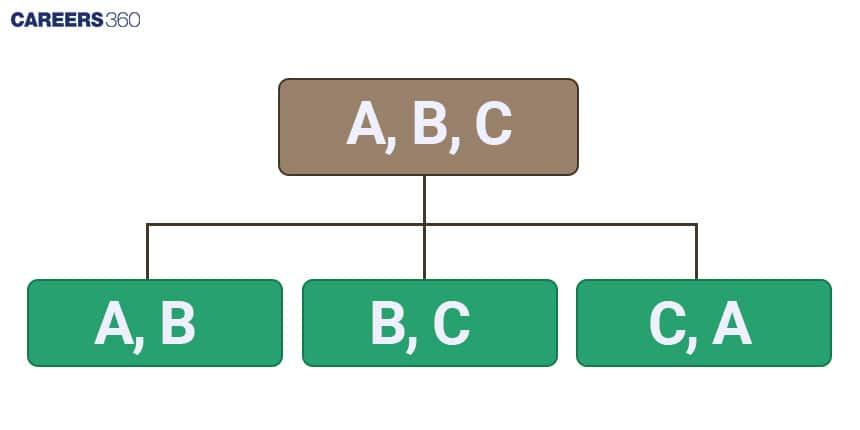
What is the Combination?
A combination is a selection of items from a larger pool, where the order of the items does not matter. In other words, it is a way of selecting items where the arrangement or sequence of the selection is not considered.
Suppose we want to select two objects from three distinct objects a, b and c. This can be stated as a number of combinations of four different objects taken two at a time.
Here we have three different combinations $ab, bc, ca, bc$. In other words, we can say that there are three ways in which we can select two objects from three distinct objects.
Combination Formula
We can generalise this concept for an $r$ object to be selected from the given $n$ objects as
$
\begin{aligned}
& { }^n C_r \times r!={ }^n P_r \\
& { }^n C_r=\frac{{ }^n P_r}{r!} \\
& { }^n C_r=\frac{n!}{(n-r)!r!}
\end{aligned}
$
Where $0 \leq r \leq n$, and $r$ is a whole number.
When is the Combination to be used?
Combinations are used when the order of selection does not matter. Here are some examples of when combinations are appropriate:
-
Lottery Selection Method: In the Lottery selection method, we use the combination method. Order does not matter in selecting lotteries to choose prize winners.
-
Forming Committees: When forming a committee from a group of people, the order in which members are chosen does not matter.
-
Choosing Subsets: When choosing a subset of items from a larger set, the order in which items are chosen is irrelevant.
-
Hand of Cards: When selecting a hand of cards from a deck, the order of the cards in the hand does not matter.
Relation between Permutation and Combination
Theorem 1: $^np_r=^nc_r × r!$
Corresponding to each combination of $^nc_r$ we have $r!$ permutations because $r$ objects in every combination can be rearranged in $r!$ ways.
Proof:
We have to prove that $^np_r=^nc_r × r!$
Taking the left side of the equation:
$^np_r=\frac{n!}{(n-r)!}$
Taking the right side of the equation
$^nc_r × r! = \frac{n!}{(n-r!) r!} × r! = \frac{n!}{(n-r)!}=^np_r$
Hence, $^np_r=^nc_r × r!$ proved.
Theorem 2: ${ }^n\mathrm{C}_r +{ }^n\mathrm{C}_{r-1} = { }^{n+1}\mathrm{C}_r$
Proof:
We have to prove that ${ }^n\mathrm{C}_r +{ }^n\mathrm{C}_{r-1} = { }^{n+1}\mathrm{C}_r$
Taking the left side of the equation, we get,
${ }^n\mathrm{C}_r +{ }^n\mathrm{C}_{r-1}$
= $\frac{n!}{r!(n-r)!}+\frac{n!}{(n-r+1)!(r-1)!}$
= $\frac{n!}{(n-r)!r(r-1)!}+\frac{n!}{(n-r+1)!(r-1)!}$
= $\frac{n!}{(r-1)!}[\frac{1}{(n-r)!r}+\frac{1}{(n-r+1)!}]$
= $\frac{n!}{(r-1)!}[\frac{1}{r(n-r)!}+\frac{1}{(n-r+1)(n-r)!}]$
= $\frac{n!}{(r-1)!(n-r)!}[\frac{1}{r}+\frac{1}{(n-r+1)}]$
= $\frac{n!}{(r-1)!(n-r)!}[\frac{n-r+1+r}{r(n-r+1)}]$
= $\frac{n!}{(r-1)!(n-r)!}[\frac{n+1}{r(n-r+1)}]$
= $\frac{(n+1)n!}{r(r-1)!(n-r+1)(n-r)!}$
= $\frac{(n+1)!}{r!(n-r+1)!}$
= ${ }^{n+1}\mathrm{C}_r$
Hence, proved.
Difference between Permutation and Combination
|
Permutation |
Combination |
|
Permutation refers to the different possible arrangements of a given number of items taken some or all at a time. |
A combination is a selection of items from a larger pool, where the order of the items does not matter. |
|
Order of arrangement is important. |
Order of arrangement is not important. |
|
Permutations are for lists. |
Combinations are for groups. |
|
The number of permutations of “$n$” objects taken “$r$” at a time is given by: $^n p_r =\frac{n!}{(n-r)!}$, Where $n$ = number of items $r$ = the number of items to be arranged |
$^n c_r =\frac{n!}{r!(n-r)!}$, Where $n$ = number of items in a collection $r$ = the number of items from the collection to be chosen |
To remember:
Permutations and Combinations in Mathematics: Solved Previous Year Questions
1) 432
2) 108
3) 36
4) 18
Solution:
No. of 4 digits number formed $= 4!$
Now each digit comes equal no. of times at unit place $= 3!$
Each digit appears at the unit place
So sum $= 3! (3+4+5+6)$
$= 6 x 18 = 108$
Hence, the answer is the option 2.
1) 160
2) 120
3) 60
4) 48
Solution:
Odd numbers: $1, 1, 3$
Even numbers: $2, 2, 2, 4, 4$
Let us first find places for odd numbers.
$1, 1, 3$ can occupy any of the 4 even positions (2^\text{nd}, 4^\text{th}, 6^\text{th}, 8^\text{th}).
Choose 3 places for them: $\binom{4}{3} = 4$
Now, $1, 1, 3$ can be arranged in these 3 places in $\frac{3!}{2!} = 3$ ways.
Number of ways for placing odd numbers: $4 \times 3 = 12$
Now, $2, 2, 2, 4, 4$ can be arranged in the remaining 5 places.
Number of ways to arrange them: $\frac{5!}{3!2!} = 10$
So, total number of ways: $12 \times 10 = 120$
Hence, the answer is $120$.
1) 72
2) 60
3) 48
4) 36
Solution:
The sum of the given digits is $0 + 1 + 2 + 5 + 7 + 9 = 24$.
Let the 6-digit number be $abcdef$.
It is divisible by 11 if $|(a + c + e) - (b + d + f)|$ is a multiple of $11$.
Only one possible case: $a + c + e = b + d + f = 12$.
Case 1: $(a, c, e) = (7, 5, 0)$ and $(b, d, f) = (9, 2, 1)$
So, $2! \times 2! \times 3! = 2 \times 2 \times 6 = 24$ ways.
Case 2: $(a, c, e) = (9, 2, 1)$ and $(b, d, f) = (7, 5, 0)$
So, $3! \times 3! = 6 \times 6 = 36$ ways.
Total ways: $24 + 36 = 60$
Hence, the answer is $60$.
1) $10^5$
2) 9 × 8 × 7 × 6 × 5
3) 90,000
4) 95
Solution:
Method 1:
We have to fill $5$ slots.
The first digit can be any from $1$ to $9$ (not $0$), so $9$ options.
Each of the remaining $4$ slots can be filled by any digit from $0$ to $9$, so $10$ options for each.
Total numbers: $9 \times 10 \times 10 \times 10 \times 10 = 90000$
Method 2:
The total ways to choose any digit for $5$ places is $10^5$.
Out of these, $10^4$ numbers start with zero (if first digit is $0$, only $4$ slots left, each with $10$ choices).
So, the count of valid five-digit numbers is $10^5 - 10^4 = 90,!000$
Hence, the answer is $90000$.
1) 7
2) 15
3) 18
4) 22
Solution:
The number of ways of selecting South Indian food $15$.
The number of ways of selecting Japanese food is $7$.
Here a person may choose any one food item, either a South Indian or a Japanese food. So, we have to use "Addition" to find the total number of ways for selecting the food item.
The total number of selecting either a South Indian or Japanese food is $15+7=22$.
Hence, the answer is option 4.
Permutation and Combinations in Different Exams
The chapter on Permutation and Combinations is an important part of Class 11 Mathematics and is frequently tested in school-level as well as competitive examinations. The table below highlights the exam-wise focus areas, commonly asked topics, and effective preparation strategies to help students prepare systematically and score better.
| Exam Name | Focus Area | Common Topics Asked | Preparation Tips |
|---|---|---|---|
| CBSE Board | Conceptual clarity & numericals | Fundamental principle of counting, permutations, combinations, and simple applications | Learn formulas and practise NCERT examples thoroughly |
| JEE Main | Problem-solving & accuracy | Permutations with restrictions, combinations, and arrangement problems | Practise MCQs and numerical-based questions regularly |
| JEE Advanced | Analytical thinking | Complex counting problems, distributions, mixed P&C concepts | Solve previous years’ advanced-level problems |
| NEET | Basics & speed | Simple permutations and combinations, counting methods | Focus on the quick application of formulas |
| State Board Exams (ICSE, UP Board, RBSE, etc) | Theory-oriented | Definitions, formulas, basic problems | Revise textbook theory and practice solved examples |
| Mathematics Olympiads | Concept application | Advanced counting techniques, challenging arrangement problems | Strengthen fundamentals and practise high-level problems |
List of topics related to Permutations and Combinations according to JEE Mains/NCERT
This section covers all the important topics from Permutations and Combinations as prescribed in the NCERT syllabus and commonly asked in JEE Main. Studying these topics systematically will help you build strong fundamentals and improve problem-solving skills.
Best Books and Resources for Permutations and Combinations
Explore top recommended books designed to strengthen your understanding and problem-solving skills in permutations and combinations. These resources are ideal for exam preparation, offering clear explanations and practice questions to help you master this topic.
| Book Title | Author/Publisher | Description |
|---|---|---|
| Permutation and Combination: Book for Boards, NTSE, IIT JEE | Ramesh Chandra | Focused on serious exam preparation with in-depth coverage. |
| Combinatorial Theory | Marshall Hall Jr. | An advanced book covering deeper combinatorics and permutation theories. |
| NCERT Class 11 Mathematics Chapter 7 | NCERT | Official textbook covering fundamental theory and problems. |
| Permutations and Combinations Book | Arihant Publication | Helpful for practice and exam preparation. |
NCERT Resources for Permutations and Combinations
NCERT resources offer simple and clear study materials for permutations and combinations. These resources help students understand key concepts easily and practice problems effectively for exams.
NCERT Subjectwise Resources
NCERT subject-wise resources provide comprehensive and well-structured study materials across all major subjects. They offer easy access to textbooks, notes, and solutions, making learning organised and effective for students at all academic levels.
| Resource Type | Mathematics | Physics | Chemistry |
|---|---|---|---|
| NCERT Notes | NCERT Notes Class 11 Maths | NCERT Notes Class 11 Physics | NCERT Notes Class 11 Chemistry |
| NCERT Solutions | NCERT Solutions for Class 11 Mathematics | NCERT Solutions for Class 11 Physics | NCERT Solutions for Class 11 Chemistry |
Practice Questions based on Permutations and Combinations
Practice questions on permutations and combinations are essential for mastering this topic. They help build problem-solving skills and improve speed and accuracy for exams.
Conclusion
Permutations and Combinations provide a strong foundation for understanding counting techniques in mathematics. With clear knowledge of definitions, formulas, and real-life applications, students can solve problems accurately and efficiently. Regular practice and concept-based learning will help in mastering this chapter and performing well in board and competitive exams.
Frequently Asked Questions (FAQs)
Q: What is permutation?
A:
A permutation is an arrangement in a definite order of a number of objects taken some or all at a time.
Q: What is the difference between permutation and combinations?
A:
Permutation is the arrangement of set of items in a specific order while combination is the selection of set of items.
Q: Write the relation between permutation and combination.
A:
Combinations can be represented in terms of permutation. The formula for permutation is $P(n,r) = \frac{n!}{(n-r)!}$. The fomula for combinations is $C(n,r) = \frac{n!}{r!(n-r)!}$ which can be rewritten as $C(n,r) = \frac{P(n,r)}{r!}$
Q: What is $n$ and $r$ in permutation?
A:
In permutation, $n$ represents the total number of items and $r$ represents the number of choosen items to be arranged.
Q: What is the formula for $nCr$?
A:
The formula for $nCr$ is $nCr = \frac{n!}{r!(n-r)!}$
Q: How to calculate permutation and combination?
A:
Permutation formula: $^nP_r = \frac{n!}{(n-r)!}$
Combination formula: $^nC_r = \frac{n!}{r!(n-r)!}$
Use permutation when order matters and combination when it doesn’t.
Articles