Definite Integrals of Piecewise Functions

Integration is one of the important parts of Calculus, which applies to measuring the change in the function at a certain point. Mathematically, it forms a powerful tool by which slopes of functions are determined, the maximum and minimum of functions found, and problems on motion, growth, and decay, to name a few. These integration concepts have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

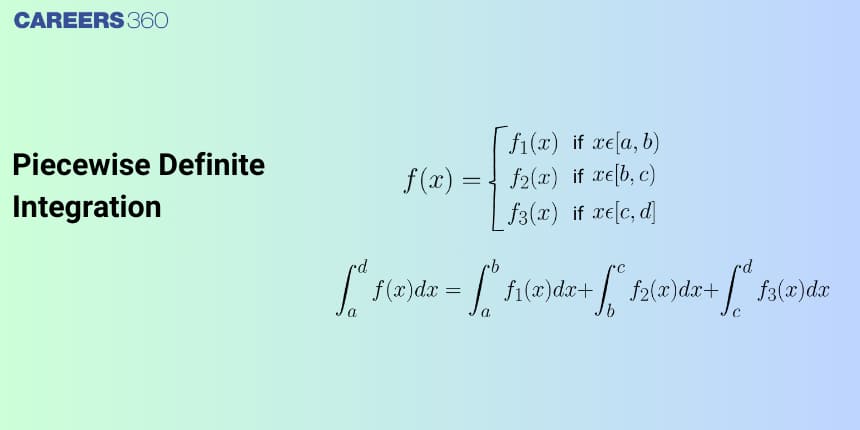
Piecewise Definite integration

Definite integration calculates the area under a curve between two specific points on the x-axis.

Let f be a function of x defined on the closed interval [a, b]. F be another function such that $\frac{d}{d x}(F(x))=f(x)$ for all x in the domain of f, then $\int_a^b f(x) d x=[F(x)+c]_a^b=F(b)-F(a)$is called the definite integral of the function f(x) over the interval [a, b], where a is called the lower limit of the integral and b is called the upper limit of the integral.

Definite integrals have properties that relate to the limits of integration.

Property 1

If the upper and lower limits of integration are the same, the integral is just a line and contains no area, hence the value is 0. $\int_a^a f(x) d x=0$

Property 2

The value of the definite integral of a function over any particular interval depends on the function and the interval but not on the variable of the integration. $\int_a^b f(x) d x=\int_a^b f(t) d t=\int_a^b f(y) d y$

Property 3

If the limits of definite integral are interchanged, then its value changes by a minus sign only.

Property 4 (King's Property)

This is one of the most important properties of definite integration. $\int_a^b f(x) d x=\int_a^b f(a+b-x) d x$

Property 5 (Piecewise Definite integration)

$\int_{\mathrm{a}}^{\mathrm{b}} \mathrm{f}(\mathrm{x}) \mathrm{dx}=\int_{\mathrm{a}}^{\mathrm{c}} \mathrm{f}(\mathrm{x}) \mathrm{dx}+\int_{\mathrm{c}}^{\mathrm{b}} \mathrm{f}(\mathrm{x}) \mathrm{dx}$ where $c \in \mathbb{R}$

This property is useful when the function is in the form of piecewise or discontinuous or non-differentiable at x = c in (a, b).
$
\begin{aligned}
& \text { Let } \quad \frac{\mathrm{d}}{\mathrm{dx}}(\mathrm{F}(\mathrm{x}))=\mathrm{f}(\mathrm{x}) \\
& \therefore \quad \int_a^c f(x) d x+\int_c^b f(x) d x \\
& =\left.\mathrm{F}(\mathrm{x})\right|_{\mathrm{a}} ^{\mathrm{c}}+\left.\mathrm{F}(\mathrm{x})\right|_{\mathrm{c}} ^{\mathrm{b}} \\
& =\mathrm{F}(\mathrm{c})-\mathrm{F}(\mathrm{a})+\mathrm{F}(\mathrm{b})-\mathrm{F}(\mathrm{c}) \\
& =\mathrm{F}(\mathrm{b})-\mathrm{F}(\mathrm{a}) \\
& =\int_a^b f(x) d x
\end{aligned}
$

The above property can be also generalized into the following form

$\int_a^b f(x) d x=\int_a^{c_1} f(x) d x+\int_{c_1}^{c_2} f(x) d x+\ldots+\int_{c_n}^b f(x) d x$

Property 6

$\int_0^a f(x) d x=\int_0^{a / 2} f(x) d x+\int_0^{a / 2} f(a-x) d x$

Proof:

From the previous property,

$
\int_0^a f(x) d x=\int_0^{a / 2} f(x) d x+\int_{a / 2}^a f(x) d x
$
Put $x=a-t \Rightarrow d x=-d t$ in the second integral, when $x=a / 2$, then $t=a / 2$ and when $x=a$, then $t=0$

$
\therefore \quad \begin{aligned}
\int_0^a f(x) d x & =\int_0^{a / 2} f(x) d x+\int_{a / 2}^0 f(a-t)(-d t) \\
& =\int_0^{\mathrm{a} / 2} \mathrm{f}(\mathrm{x}) \mathrm{dx}+\int_0^{\mathrm{a} / 2} \mathrm{f}(\mathrm{a}-\mathrm{t}) \mathrm{dt} \\
\int_0^a f(x) d x & =\int_0^{a / 2} f(x) d x+\int_0^{a / 2} f(a-x) d x
\end{aligned}
$

Recommended Video Based on Piecewise Definite Integration

Solved Examples Based on Piecewise Definite Integration:

Example 1: The integral $\int_0^\pi \sqrt{1+4 \sin ^2 \frac{x}{2}-4 \sin \frac{x}{2}} d x$ equals:

1) $4 \sqrt{3}-4$
2) $4 \sqrt{3}-4-\frac{\pi}{3}$
3) $\pi-4$
4) $\frac{2 \pi}{3}-4-4 \sqrt{3}$

Solution

As learnt in concept

Fundamental Properties of Definite integration -

If the function is continuous in (a, b ) then integration of a function a to b will be same as the sum of integrals of the same function from a to c and c to b.

$\int_b^a f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$

- wherein

$\begin{aligned} & =\int_0^\pi \sqrt{\left(1-2 \sin \frac{x}{2}\right)^2}=\int_0^\pi\left|1-2 \sin \frac{x}{2}\right| d x \\ & \int_0^{\frac{\pi}{3}} \sqrt{\left(1-2 \sin \frac{x}{2}\right)}=\int_{\frac{\pi}{4}}^\pi\left(1-2 \sin \frac{x}{2}\right) d x \\ & \left(x+4 \cos \frac{x}{2}\right)_0^{\frac{\pi}{3}}-\left(x+4 \cos \frac{x}{2}\right)^\pi \\ & =4 \sqrt{3}-4-\frac{\pi}{3}\end{aligned}$

Example 2: The value of $\int_1^a[x] f^{\prime}(x) d x, a>1$, where $[x]$ denotes the greatest integer not exceeding $x$ is
1) $a f(a)-\{f(1)+f(2)+\ldots+f([a])\}$
2) $[a] f(a)-\{f(1)+f(2)+\ldots+f([a])\}$
3) $[a] f([a])-\{f(1)+f(2)+\ldots+f(a)\}$
4) $a f([a])-\{f(1)+f(2)+\ldots+f(a)\}$

Solution

As learnt in concept

Fundamental Properties of Definite integration -

If the function is continuous in (a, b ) then integration of a function a to b will be same as the sum of integrals of the same function from a to c and c to b.

$\int_b^a f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$

- wherein

$[x]$ has to be split into integral limits.

$\int_1^a[x] f^{\prime}(x) d x$

=$\int_1^2 f^{\prime}(x) d x+\int_2^3 2 f^{\prime}(x) d x+\ldots-\ldots+\int_{[a]}^a[a] f^{\prime}(x) d x$

$\begin{aligned} & f(2)-f(1)+2 f(3)-2 f(2)+--------------- \\ = & ---------+[a] f(a)-[a] f([a])\end{aligned}$

Terms start cancelling out,

We get,

$\begin{aligned} & -f(1)-f(2)-f(3)------------------- \\ - & ---f[a]+[a] f(a)\end{aligned}$

=$=[a] f(a)-(f(1)+f(2)+\cdots-\cdots-\cdots-\cdots-\cdots([a])$

Example 3: $\int_0^{\sqrt{2}}\left[x^2\right] d x$ is

1) $2-\sqrt{2}$
2) $2+\sqrt{2}$
3) $\sqrt{2}-$
4) $\sqrt{2}-2$

Solution

Fundamental Properties of Definite integration -

If the function is continuous in (a, b ) then integration of a function a to b will be same as the sum of integrals of the same function from a to c and c to b.

$\int_b^a f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$

- wherein

$\begin{aligned} & \int_0^2\left[x^2\right] d x=\int_0^1\left[x^2\right] d x+\int_1^{\sqrt{2}}\left[x^2\right] d x \\ & \Rightarrow 0+\int_1^{\sqrt{2}} 1 d x=\sqrt{2}-1\end{aligned}$

Example 4: Choose the correct option?

1) $\int_{-a}^a f(x) d x=\int_{-a}^0 f(x) d x+\int_0^a f(x) d x$
2) $\int_a^c f(x) d x=\int_a^d f(x) d x+\int_d^c f(x) d x$; where $a<d<c$
3) $\int_a^c f(x) d x=\int_a^b f(x) d x+\int_b^c f(x) d x$; where $a<c<b$

4) All are true.

Solution

As we have learnt,

Fundamental Properties of Definite integration -

If the function is continuous in (a, b ) then integration of a function a to b will be same as the sum of integrals of the same function from a to c and c to b.

$\int_b^a f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$

- wherein

It doesn't matter if b lies between a and c or not.

Example 5: The value of the integral $\int_{-2}^2 \frac{\sin ^2 x}{\left[\frac{x}{\pi}\right]+\frac{1}{2}} d x$(where $[x]$ denotes the greatest integer less than or equal to (x) ) is :

1) $\sin 4$

2) 0

3) 4

4) $4-\sin 4$

Solution

Fundamental Properties of Definite integration -

If the function is continuous in (a, b ) then integration of a function a to b will be same as the sum of integrals of the same function from a to c and c to b.

$\int_b^a f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$

- wherein

$\begin{aligned} & I=\int_2^{-2} \frac{\sin ^2 x}{\left|\frac{1}{7}\right|+\frac{1}{2}} d x \\ & =\int_2^0 \frac{\sin ^2 x}{\frac{1}{2}} d x+\int_0^{-2} \frac{\sin ^2 x}{-1+\frac{1}{2}} d x \\ & 2 \oint_2^0 \sin ^2 x d x 1-2 \int_0^{-2} \sin ^2 x d x \\ & P u t x=-p \Rightarrow d x=-d y \sin ^2(-p)=\sin ^2 p \\ & =2 \oint_0^2 \sin ^2 x d x+2 \int_2^0 \sin ^2 P d p\end{aligned}$